School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore, E-mail: SONG0084@e.ntu.edu.sg

NG Chiu-On (吴朝安)

Department of Mechanical Engineering, The University of Hong Kong, Hong Kong, China

LAW Wing-Keung Adrian

School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore

Dispersion in oscillatory electro-osmotic flow through a parallel-plate channel with kinetic sorptive exchange at walls*

SONG Jie

School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore, E-mail: SONG0084@e.ntu.edu.sg

NG Chiu-On (吴朝安)

Department of Mechanical Engineering, The University of Hong Kong, Hong Kong, China

LAW Wing-Keung Adrian

School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore

(Received September 3, 2013, Revised February 16, 2014)

Dispersion in time-oscillatory electro-osmotic flows in a slit micro-channel under the effect of kinetic sorptive exchange at walls is theoretically investigated using the homogenization method. The two walls of the channel are considered to be made up of different materials, and therefore have different zeta potentials and sorption coefficients. A general expression for the Taylor dispersion coefficient under different zeta potentials as well as various sorption conditions at the walls is derived analytically. The dispersion coefficient is found to be dependent on the oscillation frequency, the Debye parameter, the species partition coefficient, the reaction kinetics and the ratio of the wall potentials. The results demonstrate that the presence of wall sorption tends to enhance the dispersion when the oscillation frequency is low, but the effect is negligible in high-frequency oscillatory flows. Moreover, it is found that the dispersion coefficient could be significantly changed by adjusting the relative wall potentials for low-frequency flows.

oscillatory electro-osmotic flows, dispersion, sorptive walls, homogenization method

Introduction

Electro-osmotic flow (EOF) describes the movement of fluid induced by an applied electric potential. Due to the electric double layer (EDL) effect formed at the contact interface of an electrolyte and a solid surface, the ions within the EDL migrate under the external electric field and leads to the movement of the adjacent fluid by virtue of viscous momentum transfer. As species separation and mixing in micro- and nanoscales are key components in many microfluidics applications, a number of studies have been conducted on hydrodynamic dispersion in steady EOFs, for example, dispersion in EOFs with low wall potentials[1,2], highwall potentials[3-5], dispersion due to combined pressure-driven and EOF[6], and dispersion under different temperature distribution[7].

Compared to steady flows, oscillatory EOF driven by alternating currents (AC-driven EOF) has become more and more popular due to the wide applications and huge advantages. Dispersion in pressure-driven oscillatory flows was extensively investigated in macro-scales, the dispersion coefficient was found to be dependent on the oscillating frequency, velocity magnitude, cross-sectional geometry and Schmidt number[8-10]. However, studies on dispersion in oscillatory EOFs are relatively rare. Huang and Lai[11]analyzed the mass transport driven by oscillatory EOFs in a two-dimensional micro-channel. The results demonstrated that species separation could be well achieved by proper choices of the Debye length, oscillation frequency and tidal displacement. Wang and Wu[12]examined the pressure-driven oscillatory flows in micro-channels with slippy walls and electro-viscous effect. Kuo et al.[13]studied a directional EOFdue to a nonlinear interaction between oscillatory axial electrical fields and oscillatory wall potential. Paul and Ng[14]further investigated the dispersion behavior in such kind of flows. They found that the phase of wall potential plays an important role in determining the dispersion coefficient magnitude. The minimum and maximum dispersion coefficients can be achieved when the phase difference between the two wall potentials is zero and π, respectively. In addition, wall reaction plays an important role in the dispersion in micro-scale channels. Misra and Chandra[15]studied the oscillatory EOFs in a porous micro-channel. Ghosal[16]analyzed the effect of analyte sorption on EOFs, and pointed out that the sorption of charged species at the wall could influence the zeta potential in a non-uniform manner[17]. Recently, Ramon et al.[18]investigated the dispersion in oscillatory EOFs in a cylindrical micro-tube with reactive wall by applying an approach similar to Ng[19]. It was shown that the presence of wall reaction could enhance the dispersion process.

In reality, rectangular micro-channels are typically fabricated in a way that the materials of the two parallel plates are different. As a result, a more general model which can take into account the effects of different zeta potentials and sorptions at the two walls is desirable. In the present study, the dispersion of oscillatory EOFs in a two-dimensional micro-channel with different wall potentials as well as reversible sorption effect is theoretically investigated. Results are presented to illustrate how the dispersion coefficient may depend on the various controlling parameters.

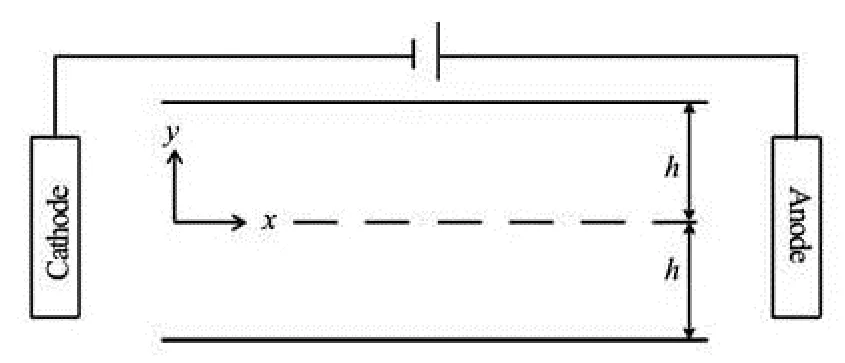
Fig.1 Schematic diagram of the system

1. Problem formulation

In the present study, we consider time-oscillatory electro-osmotic flow (EOF) between two parallel plates with possibly different wall potentials and sorptions. A sinusoidally time-varying axial electric field is imposed on the system such that oscillatory EOFs could be generated inside the two-dimensional microchannel. As is illustrated in Fig.1, a Cartesian coordinate system is used where thex-axis represents the axial direction and they-axis is perpendicular to the flow direction. The distance between the top and bottom walls is 2h. The time-varying electric fieldEis given by

whereE0is a constant amplitude,iis the complex unit, Re stands for the real part,ωis the angular frequency, andtis time.

The fluid is assumed to be isothermal, Newtonian and incompressible. In the absence of a pressure gradient, the governing equation for the flow field is

whereuis the flow velocity along the axial direction,ρthe fluid density,μthe dynamic viscosity of fluid, andeρthe electric charge density.

Now we proceed to consider the electric field. Assume that the electric charge densityeρsatisfies the Boltzmann distribution, i.e.,

with the no-slip boundary conditions at the walls

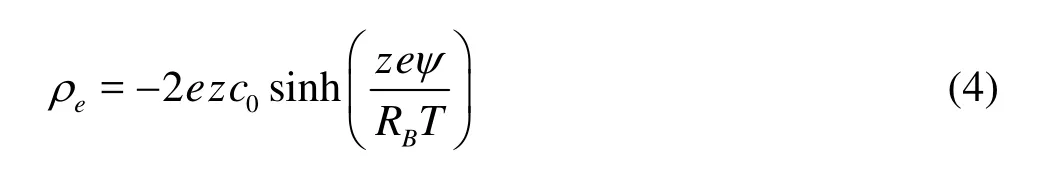
whereeis the electron charge,zis the valence of the co- and counter-ions in the carrier liquid,c0the ion concentration far from the charged walls,RBthe Boltzmann constant,Tthe absolute temperature, andψthe electric potential. Here, for the static Boltzmann distribution to be valid, the flow frequency shall be limited to around 1 MHz to avoid EDL relaxation effects[14]. The electric potential can be expressed by the following Poisson equation,

whereηis the permittivity of the liquid medium.

Substituting Eq.(4) into Eq.(5) and applying the Debye-Hückel approximation as the electric potentialψis assumed to be sufficiently small (i.e.,ψ≤25 mV), we obtain the following linear equation

The boundary conditions for Eq.(6) are prescri-bed by the wall potentials. In the present study, we consider the case where the top and bottom walls may have different potentials, i.e., Equation (6) along with Eq.(7) yields the following solution forψ

where2ψis the ratio of the two wall potentials

Substituting Eqs.(8) and (1) into Eq.(2), the governing equation becomes

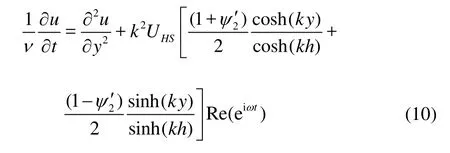
Let us introduce the following form of velocity profile

wheref(y) is a complex function ofy. Substituting Eq.(11) into Eq.(10), we obtain the governing equation forfas below

with the boundary conditions

The solution can be obtained readily as follows

2. Mass transport

For the solute dispersion, we consider that the materials of the two walls are different whereby the species in the fluid undergo reversible sorption at the top wall while the bottom wall is chemically inert. The dispersion is governed by the convection-diffusion equation, i.e.,

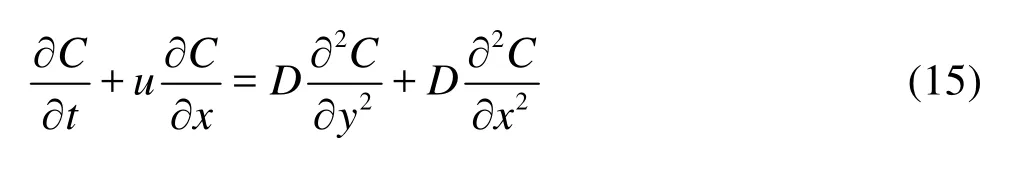
with the boundary conditions,

whereCis the concentration of the mobile phase (mass of species dissolved in unit volume of fluid),Csthe concentration of the immobile phase (mass of species adsorbed on unit surface area of wall),Dthe molecular diffusivity,κthe reaction rate constant andαa partition coefficient of the chemical. Here, we only consider the first-order reaction at the wall. Also, we assume that the wall lining is so thin that only the integrated effects across the layer need to be considered. At equilibrium,Cscan be related toCby,

We now introduce the homogenization approach with the multiple-scale perturbation analysis. For EOFs in micro-channels, the assumptions for the homogenization approach to be applicable are typically satisfied[14]. Adopting three sharply distinct time scalest0,t1andt2to represent the three different transport processes, i.e., diffusion across the channel 2 (h/D), advection along the axial direction (L/UHS), anddispersion along the axial direction2(L/D), respectively, where

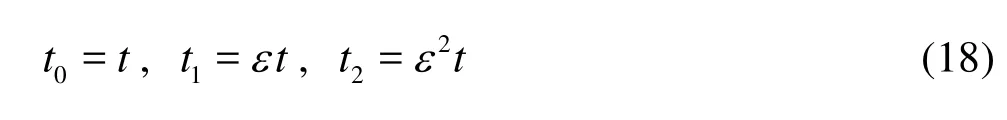
whereLis the channel length,εis a parameter much smaller than one, the relative significance of terms in Eq.(15) can be indicated byεas below

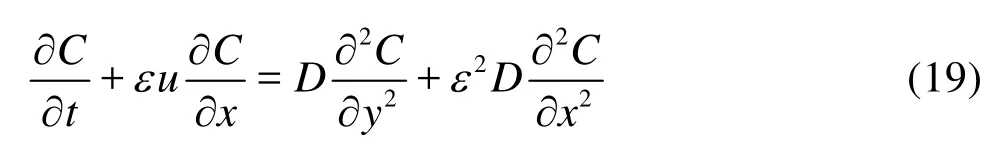
subject to the boundary conditions

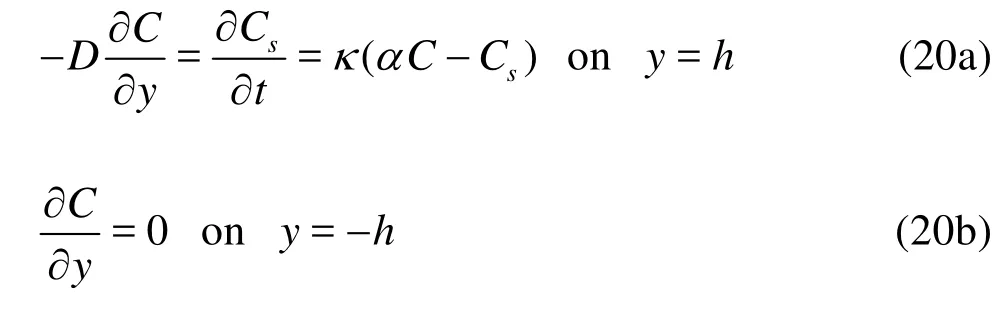
In the same manner, the concentration and the time derivative can be expanded as follows:

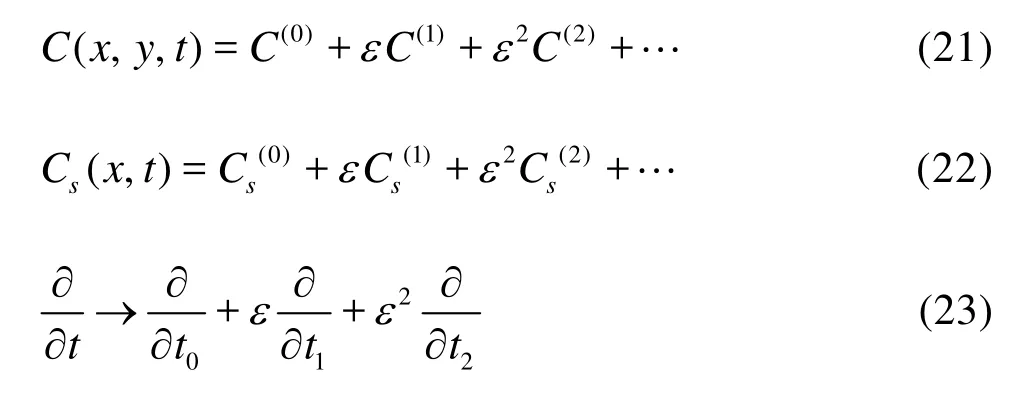
At the leading orderO(1), Eq.(19) becomes

with the boundary conditions

Equations (24) and (25b) imply that

Also, Eq.(25a) suggests

AtO()ε, the concentrationC1is governed by

and the boundary conditions become

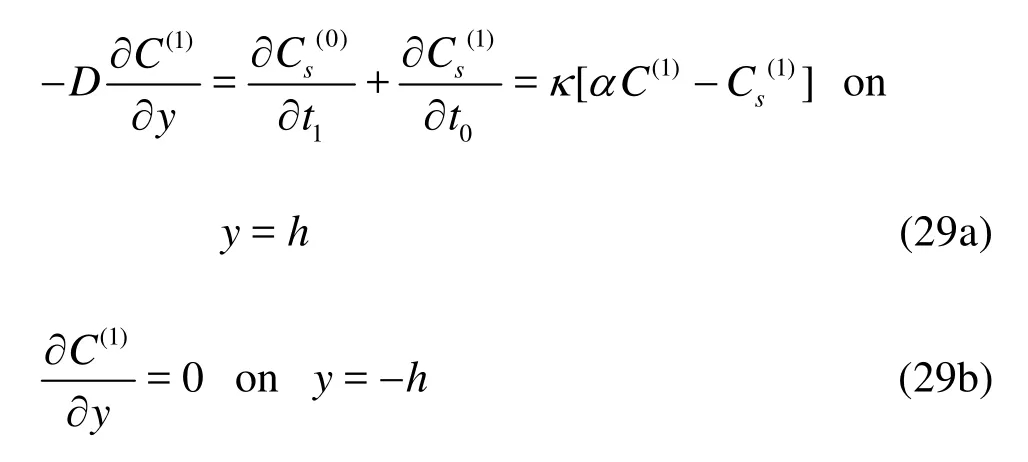
Taking time and cross-sectional average of Eq.(28), we obtain

Substituting Eq.(30) back into Eq.(28) leads to

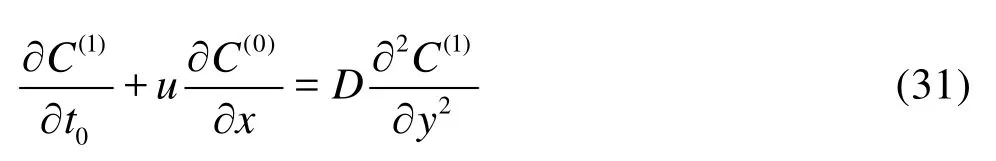
with the boundary conditions

In view of linearity, the first-order concentrationC1can be expressed as

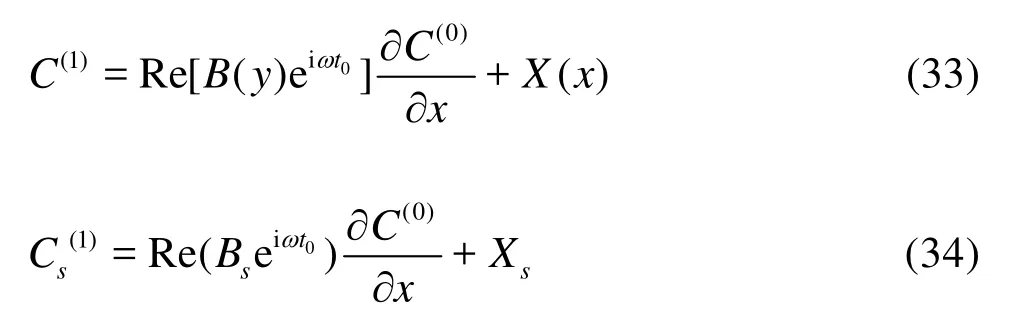
whereBis a complex function ofythat will be derived later.

AtO(ε2), Eqs.(19) and (20) give

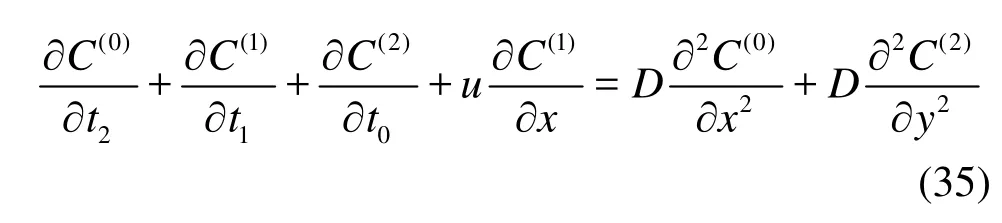
with the boundary conditions

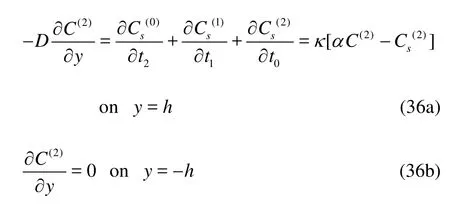
Taking time and cross-sectional average of Eqs.(35), (36a) and (36b), we obtain

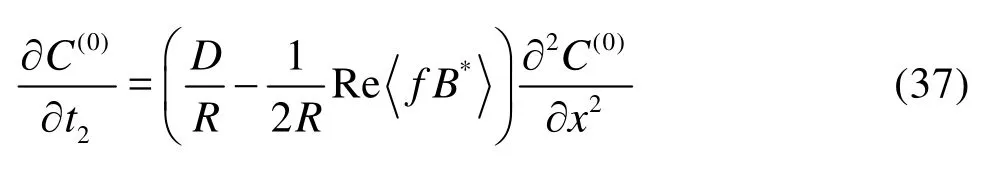
whereR=1+α/2his the retardation factor, the angular brackets<> denote the cross-sectional average and the asterisk denotes the complex conjugate. Hence,

is a dispersion coefficient due to the oscillatory flow. Now we proceed to solve the functionB, which is the key towards the determination of the dispersion coefficient. To better illustrate the problem, we introduce the normalized parameters as below,

It is easy to expressf＇ in non-dimensional form as

with the boundary conditions

is the Damkohler number.

The solution of Eq.(41) can be obtained as

The unknown parametersC1andC2can be determined by applying the boundary conditions. Their expressions are presented in Appendix.

2.1Particular Case (1)

For the particular case where the electric potential of the two walls are the same, i.e.,ψ2＇=1, Eq.(44) can be simplified to

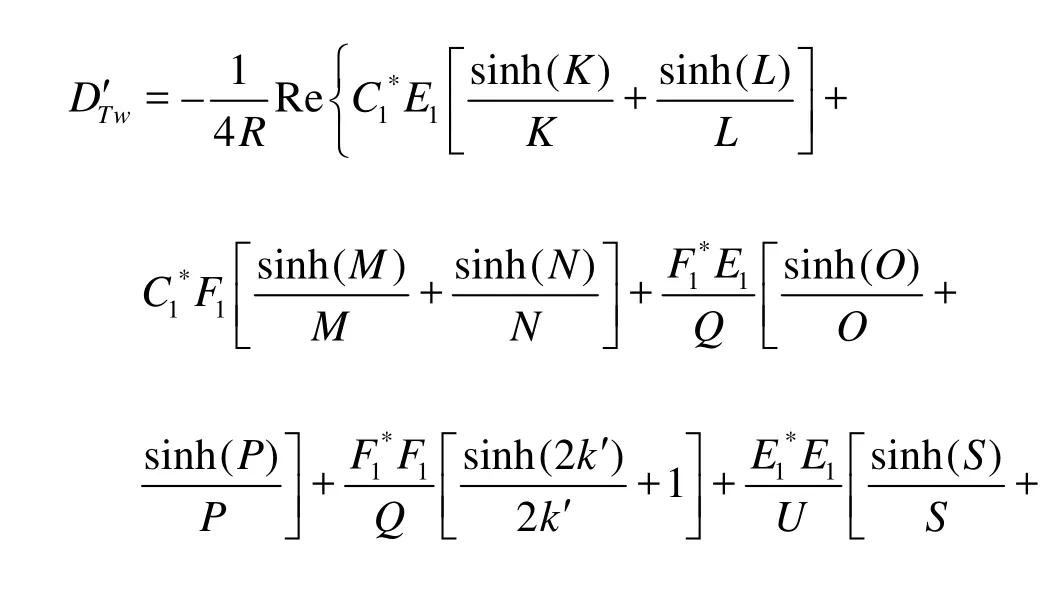
2.2Particular Case (2)

For the case where the two wall potentials are the same and no sorption occurs at both walls, the form of the dispersion coefficient remains the same as Eq.(45) withC1becomes

The derived result is the same as the dispersion coefficient due to the interaction of the oscillatory electric field with the steady component of the wall potentials presented by Paul and Ng[14].

2.3Particular Case (3)

For the case that the two wall potentials are identical and symmetric sorption occurs at both walls,Rin Eq.(45) becomesR=1+α＇, and the boundary conditions (42b) changes to

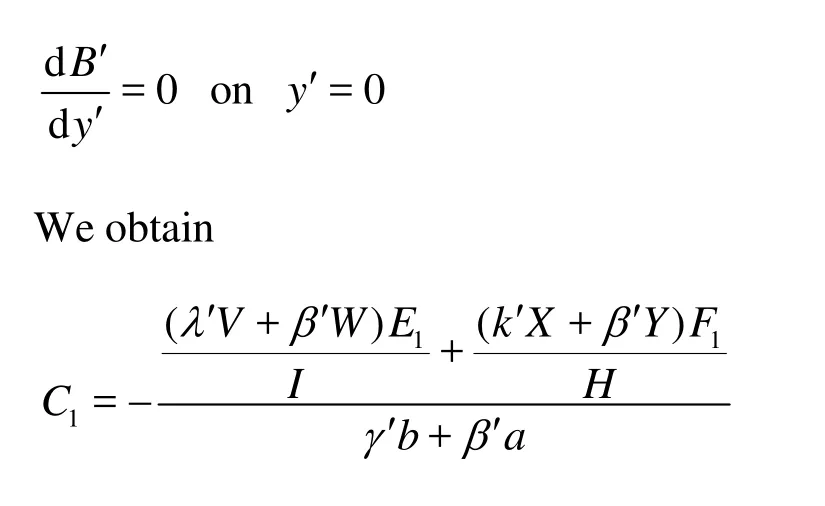
3. Results and discussion

We evaluate the dependence of the dimensionless

Fig.2 Scaled velocity profiles at various times within an oscillation forψ2＇=1 and =1000Sc

dispersion coefficientDT＇won various dimensionless parameters as illustrated below. We first review the physical significance of these parameters.δ＇=δ/h=is the dimensionless Stokes boundary layer thickness. For flow with higher oscillation frequency, the Stokes boundary layer is thinner andδ＇ is smaller, and vice versa. By recalling the definitions ofλ＇ andγ＇, one finds thatδ＇ is inversely proportional toλ＇ andγ＇, i.e.,λ＇=(1+i)/δ＇ andi)/δ＇, whereSc=ν/Dis the Schmidt number which is fixed to be 1000 in the present study. The EOF allows a wide range of frequencies, typically below ~1 MHz as stated before, and thus a wide range of the Stokes boundary layer thickness will be considered in the following, i.e.,O(0.1)～O(10).k＇ characterizes the EDL thickness and smallerk＇ implies larger Debye length. Typically, the value ofk＇ is large, i.e.,O(10)～O(100).α＇ denotes a normalized partition coefficient of the species,Dasignifies the reversible sorption rate where largerDaimplies faster phase exchange kinetics, and2ψ＇ represents the potential of the bottom wall relative to that of the top wall, which is kept between -1 and 1.

The velocity profile is governed by the Stokes boundary layer thickness, the Debye length as well as the wall potentials. Figure 2 shows the velocity profiles at different times within an oscillation cycle when

the potentials at the two walls are the same, i.e.,ψ2＇=1, where the dimensionless velocityu＇=u/UHS. It can be seen that for the flow with a high frequency, the velocity varies significantly near the wall due to the viscous effect, and becomes almost a constant (zero) in the core region due to inertia. Asωdecreases, the velocity profile becomes more uniform and finally turns to a “plug flow” profile as that of a steady EOF whenδ＇ reaches 10. The effect of Debye length is obvious; ask＇ increases, the plug-like core region of the flow increases in size. For the conditions that the wall potentials are different, the velocity profiles become asymmetrical about the centerline but possess similar trends (not shown).

Fig.3 Dispersion coefficientDT＇was a function ofδ＇ fork＇= 100,ψ2＇=1,α＇=1 and =1000Sc

We next proceed to evaluate the dispersion coefficient induced by the oscillatory EOFs with the presence of wall sorption effect. Ramon et al.[18]investigated the dispersion in a circular channel with low oscillating frequency where the flow behaves as a plug flow. In the present study, we consider a much wider range of the oscillating frequency. Figure 3 shows the variation ofDT＇wwith the Stokes boundary layer thicknessδ＇ under different wall reaction conditions. It is obvious that the dimensionless dispersion coefficientDT＇wincreases withδ＇ significantly. It suggests that keeping the velocity amplitude unchanged, the dispersion coefficient is enhanced by reducing the oscillation frequency. This is reasonable as the tidal displacement increases asωdecreases and thus leads to stronger mass transfer. One thing needs to be noted is that by fixing the tidal displacement, the dispersion coefficient increases with the oscillation frequency due to the fact that the flow velocity increases as the frequency increases. Figure 3 also compares the values ofDT＇wunder various wall sorption conditions, i.e., no sorption at either wall, sorption at the top wall only and symmetric sorption at both walls. The results demonstrate that the presence of wall sorption could enhance the dispersion process: the faster the reaction kinetics, the stronger the dispersion whenδ＇ is large. This may be attributed to the fact that wall sorption allows for a greater temporal storage and thus enhances the mass transfer under appropriate flow conditions[18]. However, for smallδ＇, i.e.,δ＇ less than around 2, the difference among different sorption conditions is almost negligible. It suggests that for highfrequency oscillatory flows, the effect of reactive wall on the longitudinal dispersion is very small due to the too short time for reaction.

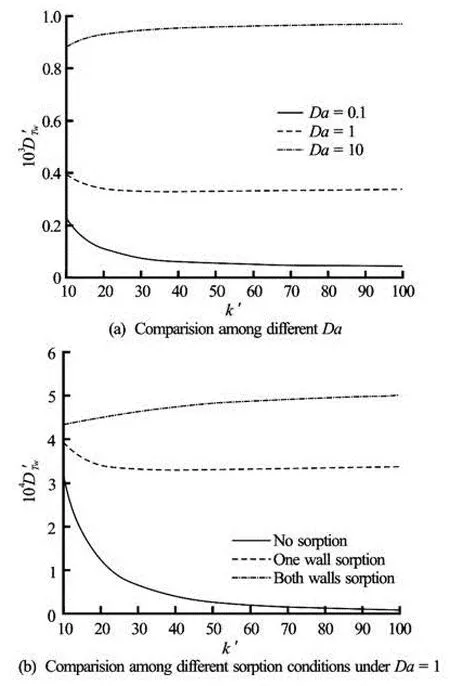
Fig.4 Dispersion coefficientDT＇was a function ofk＇ forδ＇= 10,ψ2＇=1,α＇=1 and =1000Sc

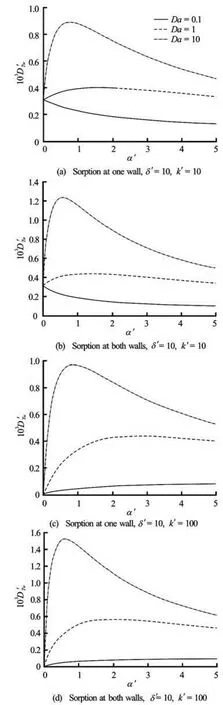
Fig.5 The variation ofDT＇wwithα＇ forψ2＇=1 andSc= 1 000

Stokes boundary layer, i.e.,δ＇=0.1, the dimensionless dispersion coefficient decreases with the EDL thickness. As can be seen from Figs.2(a) and 2(b), theψ2＇=1. The effect of the relative wall potential on the dispersion coefficient under different wall sorption conditions is shown in Fig.6. Figures 6(a) and 6(b) demonstrate the conditions of high-frequency flows, where a minimum dispersion coefficient is achieved atψ2＇=0 for most cases (ψ2＇=0.18 for both walls sorvelocity profile varies more significantly near the boundaries when the EDL thickness is thinner. Also, the reaction kineticsDahas almost no influence on the dispersion in a high-frequency oscillatory EOF (not shown). For the condition of “plug flow”,k＇ has different effect on the dispersion coefficient depending on the wall sorption conditions:DT＇wtends to increase with the Debye length when there is no sorption. Different from high-frequency flow, as can be seen from Figs.2(e) and 2(f), the velocity profile is flatter at a largerk＇, and hence, the dispersion coefficient is limited when the Debye length is short. For the conditions of presence of wall sorption, the “temporal storage” effect of wall sorption dominates the dispersion and weakens the effect of Debye length. This explains why under a particularDathe dispersion coefficient varies slightly with the Debye length.

The partition coefficient is a chemical constant of the species. Similar to Fig.3, it is found that as the normalized partition coefficientα＇ increases from 0 to 5, the dispersion coefficient declines with a decreasing rate whenδ＇ is small, and the difference among variousDais negligible as well (not shown). For “plug flow” with largeδ＇, the effect ofα＇ onDT＇wrelies on the value ofDa. Figure 5 illustrates the relationship betweenDT＇wandα＇ under various conditions. It is observed thatDT＇wincreases withα＇ and then decreases with a peak occurring atα＇≈1 at largeDa, i.e.,Da=10, for all cases. However, the effect ofα＇on the dispersion coefficient is not obvious whenDais small. Comparing the conditions of single wall and both walls sorption, i.e., Figs.5(a) and 5(b), and Figs.5(c) and 5(d), one finds that there is no big difference for the dispersion coefficient at smallDa, however, both walls sorption could induce relatively stronger dispersion than single wall sorption whenDais large, especially at the peak. The existence of the peak indicates that, to separate two chemicals with different reaction rate, one could adjust the non-dimensional partition coefficientα＇ of the chemical with largerDato be around 1.

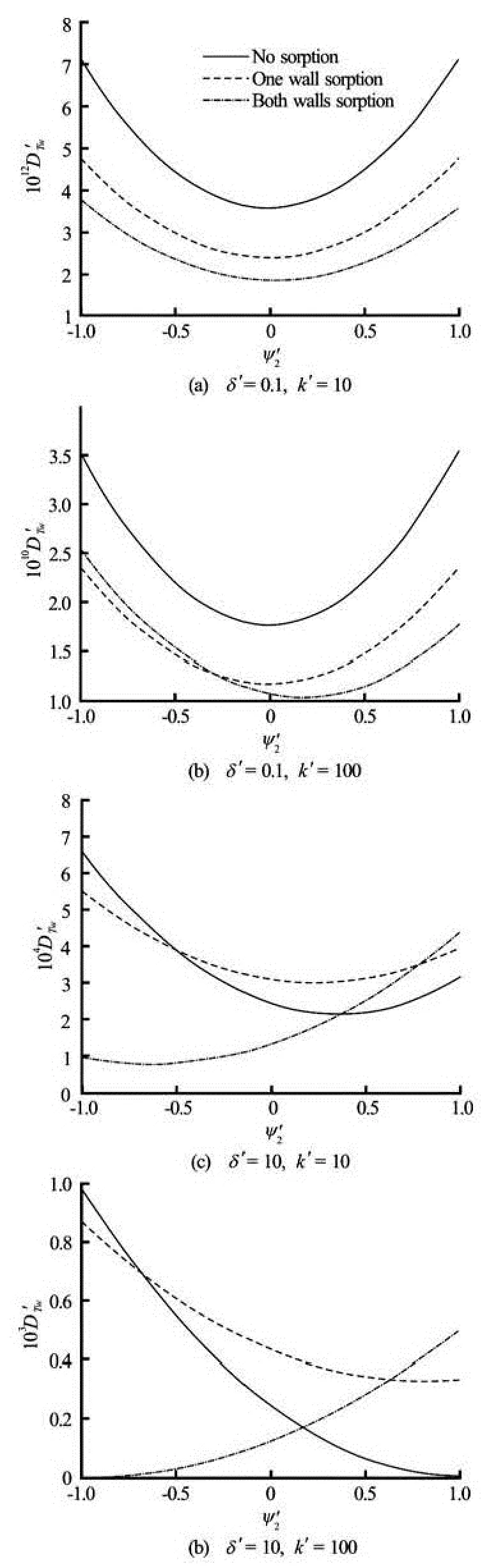
Fig.6 The relationship between the relative bottom wall potential2ψ＇ and the dispersion coefficient under different sorption conditions forα＇=1,Da=1 and =1000Sc

The results presented above are all based on the condition of the same potential at both walls, i.e., ption in Fig.6(b)). The reason is that when the potential of the bottom wall is zero, the flow velocity varies near the top wall only while keeps zero at the rest area, which leads to a more limited velocity shear across the channel. It also suggests that the variation of dispersion coefficient induced by changing the relative wall potential is tiny for high-frequency flows as the magnitude ofDT＇wis extremely small in Figs.6(a) and 6(b). The conditions of low-frequency flows, where the flow behaves like a slowly varying steady flow, are illustrated in Figs.6(c) and 6(d). Basically,DT＇wtends to increase asψ2＇ changes from -1 to 1 for the case of sorption at both walls but decrease for the cases of no sorption and single wall sorption. The minimum ofDT＇w, as shown in Fig.6(c) for the cases of no sorption, one wall sorption and both walls sorption, occurs atψ2＇=0.35, 0.24 and -0.63, respectively. The results in Figs.6(c) and 6(d) indicate that for the condition of opposite wall potentials, i.e.,ψ2＇=–1, the presence of wall sorption tends to have reversed effect on the dispersion.

4. Conclusions

In the present paper, dispersion in oscillatory EOFs between two parallel plates with reversible sorption effect has been analytically studied. A general expression for the non-dimensional dispersion coefficient has been derived through the homogenization technique. The results show that keeping the velocity amplitude constant, the dispersion coefficient decreases with the oscillation frequency significantly. The presence of reversible sorption at the walls could influence the dispersion coefficient in a complicated manner: generally, the effect is not obvious for highfrequency flows, while for low-frequency flows, the existence of wall sorption tends to enhance the dispersion and the enhancement is proportional to the reaction rate.

The effect of disparate wall potentials on the dispersion coefficient has also been examined. It is found that the dispersion could be minimized by making the bottom wall potential approach zero for highfrequency flows even though the change is small. For low-frequency flows, the opposite wall potentials could lead to the strongest dispersion for the case of no sorption but the weakest dispersion for the case of sorption at both walls.

The present analytical study provides a guideline for the microfluidic system design for various applications. For example, for low-frequency oscillatory flows, the dispersion coefficient is a strong function of the sorption effects when the chemical partition coefficientα＇=α/h≈1, and hence, chemical separation for species with different wall reaction rates could be achieved by adjusting the channel dimensions and materials. Furthermore, mixing in micro-devices can speeded up/slowed down by changing the electric potentials of both the top and bottom walls according to the sorption conditions.

References

[1] MCELDOON J. P., DATTA R. Analytical solution for dispersion in capillary liquid chromatography with electroosmotic flow[J].Analytical Chemistry,1992, 64(2): 227-230.

[2] GRIFFITHS S. K., NILSON R. H. Hydrodynamic dispersion of a neutral nonreacting solute in electroosmotic flow[J].Analytical Chemistry,1999, 71(24): 5522-5529.

[3] ANDREEV V. P., LISIN E. E. Investigation of the electroosmotic flow effect on the efficiency of capillary electrophoresis[J].Electrophoresis,1992, 13(11): 832-837.

[4] GAS B., STEDRY M. and KENNDLER E. Contribution of the electroosmotic flow to peak broadening in capillary zone electrophoresis with uniform zeta potential[J].Journal of Chromatography A,1995, 709(1): 63-68.

[5] GRIFFITHS S. K., NILSON R. H. Electroosmotic fluid motion and latetime solute transport for large zeta potentials[J].Analytical Chemistry,2000, 72(20): 4767-4777.

[6] ZHOLKOVSKIJ E. K., MASLIYAH J. H. Hydrodynamic dispersion due to combined pressure-driven and electroosmotic flow through microchannels with a thin double layer[J].Analytical Chemistry,2004, 76(10): 2708-2718.

[7] ZHANG Kai, LIN Jian-zhong. The effect of temperature distribution on the mass species transport in microchannels driven by electroosmosis[J].Journal of Hydrodynamics, Ser. B,2006, 18(3): 65-70.

[8] ARIS R. On the dispersion of a solute in pulsating flow through a tube[J].Proceedings of the Royal Society of London, Series A-Mathematical and Physical Sciences,1960, 259(1298): 370-376.

[9] CHATWIN P. C. Longitudinal dispersion of passive contaminant in oscillatory flows in tubes[J].Journal of Fluid Mechanics,1975, 71: 513-527.

[10] WATSON E. J. Diffusion in oscillatory pipe-flow[J].Journal of Fluid Mechanics,1983, 133: 233-244.

[11] HUANG H. F., LAI C. L. Enhancement of mass transport and separation of species by oscillatory electroosmotic flows[J].Proceedings of the Royal Society A,2006, 462(2071): 2017-2038.

[12] WANG Lei and WU Jian-kang. Periodical pressure-driven flows in microchannel with wall slip velocity and electro-viscous effect[J].Journal of Hydrodynamics,2010, 22(6): 829-837.

[13] KUO C. Y., WANG C. Y. and CHANG C. C. Generation of directional EOF by interactive oscillatory zeta potential[J].Electrophoresis,2008, 29(21): 4386-4390. [14] PAUL S. and NG C. O. Dispersion in electroosmotic flow generated by oscillatory electric field interacting with oscillatory wall potentials[J].Microfluidics Nanofluidics,2012, 12(1-4): 237-256.

[15] MISRA J. C., CHANDRA S. Electro-osmotic flow of a second-grade fluid in a porous microchannel subject to an AC electric field[J].Journal of Hydrodynamics,2013, 25(2): 309-316.

[16] GHOSAL S. Effect of analyte adsorption on the electroosmotic flow in microfluidic channels[J].Analytical Chemistry,2002, 74(4): 771-775.

[17] GHOSAL S. The effect of wall interactions in capillaryzone electrophoresis[J].Journal of Fluid Mechanics,2003, 491: 285-300.

[18] RAMON G., AGNON Y. and DOSORETZ C. Solute dispersion in oscillating electroosmotic flow with boundary mass exchange[J].Microfluidics Nanofluidics,2011, 10(1): 97-106.

[19] NG C. O. Dispersion in steady and oscillatory flows through a tube with reversible and irreversible wall reactions[J].Proceedings of the Royal Society A,2006, 462(2066): 481-515.

Appendix

Expressions forC1andC2in Eq.(43) are given as follows

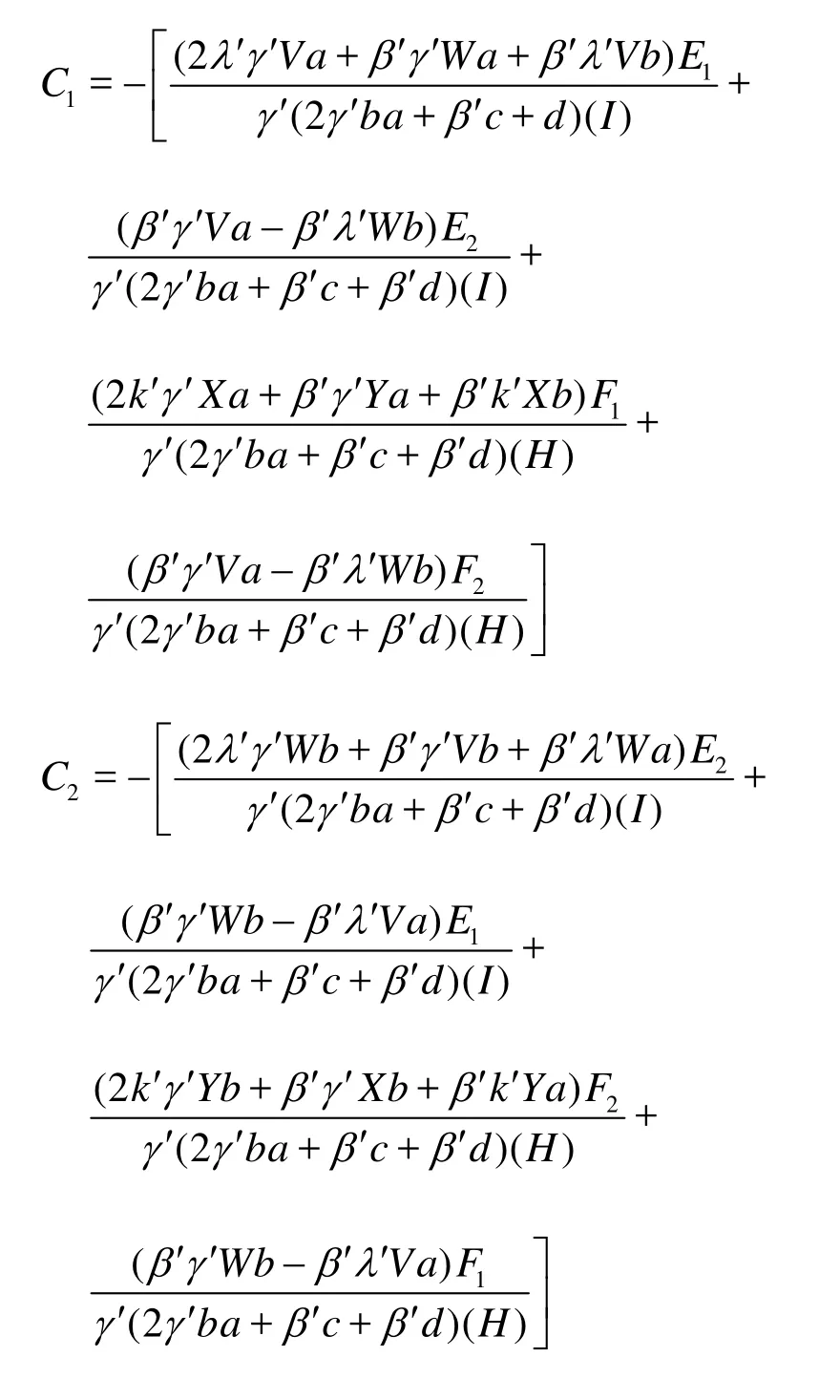
10.1016/S1001-6058(14)60041-X

* Project supported by the Research Grants Council of the Hong Kong Special Administrative Region, China (Grant No. HKU 715510E).

Biography: SONG Jie (1988-), Female, Ph. D. Candidate

NG Chiu-On, E-mail: cong@hku.hk