骆世广，骆昌日

(1．广东金融学院应用数学系，广东广州510521;2．华中师范大学职业与继续教育学院，湖北武汉430079)

文献［1］介绍了一类含有非线性梯度项的抛物方程，即方程可写为如下形式:

并给出如下初边值条件:

部分学者研究了在 Dirichlet边界条件下和Neumann边界条件的解的爆破问题［4-8］．其中考虑在Robin边界条件下解的爆破问题［9-10］．本文继续在Robin边界条件下考虑爆破问题．众所周知，p≤2q时解在有限时间内将不会爆破［11］，但是在p＞2q时，解可能会爆破［6］．本文仅考虑其特殊情况q=1时，为了简单起见，令p=s+1，那么原方程组可写为如下形式:

Robin边界条件和初值条件可写为:

其中k是一个正常数．应用抛物方程的最大值原理［12-13］得到u将是非负的，对任意的x，t［0，t*)．下面将推导出当爆破发生时，解的爆破时间的下界．

推导下界的过程中，将对式(4)中的一些数据项加适当的假设．我们可以得到如下定理:

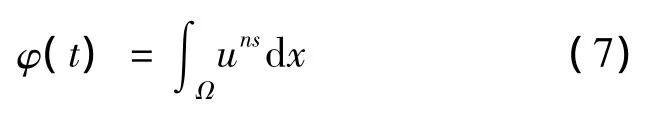
将满足如下的微分不等式

从式(8)可以得到爆破时间t*的下界，得到:

其中m4

参数τ0，L，ε3均为正常数，证明过程中将会给出其具体定义和解释．

现在开始证明定理1．首先计算

式(10)的计算过程中用到了散度定理，并且关于u的边界条件注意到如下事实:

为了方便，假设w=u(ns+1)/2，那么式(10)的最后一项可以写成

由广义的Poincare不等式推得

本文研究和应用的人工免疫故障诊断及预警算法主要包括3部分: 系统初始化，包括正常抗体库和故障抗体库的初始化；系统自学习，包括正常抗体库和故障抗体库的更新；在线故障诊断，包括故障检测和故障类别诊断。实际的在线故障诊断流程如图5所示[12-13]。

其中λ1是如下问题的第一正的特征值Δω+λω=0，+kω =0，x∂Ω，应用条件(5)，由式(12)

可得

其中m1=k(ns+1)/2．接下来处理式(13)的最后一项．由散度定理可得

其中ni是∂Ω的朝向外面的法向量的第i个分量．因为Ω是凸的，定义，则

上式推导过程中用到几何平均值不等式，且ε1是一个任意的正常数．联立式(13)、(15)，可得

对Ω和n加限制条件使得它满足λ1-3m1/τ0＞0，然后选择足够小的 ε1使之满足λ1-3/τ0-(d/τ0)2ε1＞0．由式(16)可得，其中

是一个正常数．因此，由式(10)得到

其中 m3=nsm2［2/(ns+1)］2．假设 α =1/s和 v=us，并且使用Hölder's不等式得到

运用不等式 arbq≤ra+qb，r+q=1，a，b ＞0，可得

其中 ε2是 一 个 任 意 的 正 常 数，且 L=使用积分不等式(文献［5］的式(2．16))，得到

其中m6=，且ε3是一个任意的正常数．取 ε2=，由式(17)，

可得

对式(21)从0到t积分，可得t，从中导出t*的一个下界，即其中 φ(0)= ∫Ω［f(x)］nsd x．由此证明了定理1是成立的．

注1 从定理1推导过程可知，定理1的结论对于Neumann边界条件下仍然是适用的．

［1］CHIPOTM，WEISSLER F B．Some blow up results for a nonlinear parabolic problem with agradient term［J］．SIAM JMath Anal，1989，20:886-907．

［2］KAWOHL B，PELETIER L A．Observations on blow up and dead cores for nonlinear parabolic equations［J］．Math Z，1989，202:207-217．

［3］PAYNE L E，SONG J C．Lower bounds for blow-up time in a nonlinear parabolic problem［J］．JMath Anal Appl，2009，354:394-396．

［4］PAYNE L E，SCHAEFER PW．Lower bounds for blowup time in parabolic problems under Dirichlet conditions［J］．JMath Anal Appl，2007，328:1196-1205．

［5］PAYNE L E，SCHAEFER PW．Lower bounds for blowup time in parabolic problems under Neumann conditions［J］．Applicable Analysis，2006，85:1301-1311．

［6］PAYNE L E，SONG JC．Lower bounds for the blow-up time in a temperature dependent NavierCStokes flow［J］．J Math Anal Appl，2007，335:371-376．

［7］SONG JC．Lower bounds for blow-up time in a nonlocal reaction-diffusion problem［J］．Applied Mathematical Letters，2011，24:793-796．

［8］刘晓薇，林长好．一类拟线性抛物方程的空间BLOWUP及衰减估计［J］．华南师范大学学报:自然科学版，2006(3):19-24．

［9］LIY F，LIU Y，LIN C H．Blow-up phenomena for some nonlinear parabolic problems undermixed boundary conditions［J］．Nonlinear Analysis:Real WorldApplications，2010，11:3815-3823．

［10］PAYNE L E，SCHAEFER PW．Blow-up in parabolic problems under Robin boundary conditions［J］．Applicable Analysis，2008，87(6):699-707．

［11］SOUPLET P．Recent results and open problems on parabolic equations with gradient nonlinearities［J］．Electron JDifferential Equations，2001，2001(20):1-19．

［12］FRIEDMAN A．Remarks on the maximum principle for parabolic equations and its applications［J］．Pac JMath，1958，8:201-211．

［13］NIRENBERG L．A strong maximum principle for parabolic equations［J］．CommuPur Appl Math，1953，6:167-177．