刘玉萍

近几年, 随着数学教学中“问题解决”的提出,数学教学的改革在不断深化,全国各地中､高考试卷逐渐渗透一些格调清新､别开生面的开放性试题,加大了知识间的联系,突出综合性,较好地发挥了选拔功能｡这种试题目前被认为最富有教育价值､最能开拓学生思维的问题｡

数学开放性问题是相对传统封闭题而言,或者条件不完全确定的､或者结论不唯一 ､甚至没有标准答案的问题｡

1.开放性问题的特点:

1.1可接受性

开放性问题起点低､层次多､答案不唯一､解题策略多样化｡如:①边长为12厘米的正方形可以分割为几个边长为整数的正方形?②给一个直角型的楼梯铺上地毯,需要测量哪些数据?这些问题与生活较接近,学生较熟悉,容易主动接受,易产生一种"试一试"的心理｡他们的答案有些易找到,有的较难,每个学生都有参与解决问题的机会,都愿意通过尝试解决问题去获得一些知识或者学习方法｡这种可接受性,使开放性问题还能引发多层次学生的参与｡如:用2根相等的长棒,2根相等的短棒,摆成一个四边形,你能摆几种图形?对这类问题,基础差的学生能得出简单的图形,而基础好的学生则能有序地考虑问题,尽量避免答案的重复与遗漏｡而且答案的完整性,更能反映学生的思唯层次｡举举手,能摘到果子;跳一跳,能摘到更多､更好的果子｡恰当地运用开放性问题,对培养学生的数学兴趣,激发他们学习的动机,具有积极的作用｡教师可恰当地布置一些开放性问题,给学生充分的思考时间与活动空间去解决,让他们充分享受收获的喜悦｡并在课堂上让学生交流不同的解题方法,展示解题思路,从而发现学生的学习潜能,进一步加以挖掘､培养,让学生的“果子”越摘越多,越摘越好,让他们感受到,原来觉得枯燥无味的数学,学起来竟是这样的其乐无穷,越学越想学,越学越爱学,越学越会学｡这样,学生的主动性便可充分地发挥出来｡

1.2障碍性

开放性问题由于答案不唯一,题型新颖,题目涉及面较广,没有现成的解题模式可套用,其条件可能不完善,需要在解题过程中不断完善,不断假设条件,因此,学生不能一眼看出答案,学生必须从实际问题中抓住本质,提炼成数学问题,用数学思想去思考,用数学方法去解决｡

如:某文具店出售每册为122元和80元的两种纪念册,两种纪念品每册都有30%的利润,但每册122元的不好出售,某人用1095元钱欲买一定数量的122元的纪念册｡店经理虽然发现钱不够,但认为所获得的利润比出售同册数的80元的纪念册获利还多,因此成交了这笔生意｡请问:此人欲买多少册122元纪念册?

评析:这是一道关于商家如何灵活经营,以获取最大利润的问题｡首先,此人欲买几册?条件没给出｡再者,册数是一整数,这一隐含条件,学生不易想到,而隐含条件在解题过程中,何时用上,更是解题的难点｡学生只有认真分析题意,从实际问题中抓住本质:出售x册122元的利润比出售x册80元的利润还多,建立数学模型,由 1095-122×(1-30% )X > 80× 30% X (由于客人钱不够,因此X >1095/122),再利用x的整数性质,解得x为9或为10｡

开放性问题条件的不完备或结论不唯一等特点,虽然常给解题造成一定的障碍,但从另一方面,却促使学生在解决问题的过程中,要通过观察､猜测､检验､修正､证明､推广等各种数学方法去揭示问题的关键｡这一过程不仅需要丰富的想象力､敏锐的思维能力,去及时发现可利用的条件,而且长时间的钻研,需要足够的耐心和细致,突破难点更需要足够的意志和毅力｡可见,开放性问题障碍性,有利于培养学生的学习能力,还有利于培养他们的学习品质,在促进智力因素发展的同时,也促进非智力因素的发展｡

1.3探索性

开放性问题的结论常是丰富多彩的,非单调的,而解题模式､解题途径的多样性,决定了必须从全方位,多角度去观察､分析,充分揭示问题的本质特征,达到解决问题的目的｡如:一个因数是18,另一个因数2分别扩大5倍､10倍､100倍,积怎样变化?再如:有一棱长为2厘米的正方体,将它沿某些棱剪开,有几种展开图?这个问题的条件并没有规定用何种方式剪,思维的策略不同决定裁剪的方式不同,引发多种解题方法与结论｡再如:两个人轮流报数(自然数),报出的数不能超过8,把两人报的数加起来,谁报数后加起来的数是88(或88以上的数),谁就获胜｡如果让你先报数,第一次报多少就一定获胜?这个问题则应该通过不断的探索､找规律,从而得出这个数为7｡

开放性问题的探索性,有利于促进学生的创造性思维的发展｡首先,开放性问题情景的创设,使学生置身于知识发展过程中,发现差异,提出疑问,主动带着怀疑的眼光去发现问题,造成知识冲突,教师启发诱导,让学生进入更深一层的思维;其次,及时展示思维过程,让学生观察､类比､总结,从中找出异同点;同时,组织适当的问题链,利用问题链所具有的联系性和发散性,引发学生通过对问题追根刨底的探索,达到创造性思维开发的目的｡如:讲授定理:三角形内角和等于180°时,教师启发学生思考:三角形的外角和等于多少?进一步问:四边形的外角和呢?n边形的内角和与外角和又为多少?有何规律?让学有余力的学生去摸索｡再如:一个街区有3条横街､3条纵街,如图①一个人从左上角A处出发依最短途径走到右下角B处,共有多少种不同的走法?若街区有5条横街,5条纵街,如图②又将有几种走法呢?

评析:通过观察,在多数街道的交叉口,按照最短途径的要求,行人都只有两种选择:向右横走或向下走纵街,图(1)较为容易求得6种情况,可图(2)具体计算则不胜其繁,但只要类比图(1),找出规律:行人从A——B均由4段横街和4段纵街构成,因此,每一种走法都对应一种这4横4纵的有序排列,反之亦然,因此,所求的不同最短途径数就等于 8!/4!4!=70种｡

2.开放性问题的类型:

2.1条件开放型

即问题的条件不完备或满足结论的条件不唯一｡如:姐姐买苹果花了50元钱,售货员找给8元钱,你知道姐姐买了几斤苹果吗?题中没给出苹果的单价,因此答案不唯一｡又如:某校向希望工程捐款活动中,甲班的m个男生和11个女生的捐款总数与乙班的9个男生和n个女生的捐款总数相等,都是(mn+9m+11n+145),已知每人的捐款数相同,且都是整数元,求每人的捐款数及m､n的值(96年全国初中联赛试题)｡此题可设每人捐款数为x元,据每人的捐款数及每班的捐款数均为不变量,列不定方程组:mx+11x = 9x+nx = mn+9m+11n+145再利用整数的性质得(1)m=35,n=37,x=47;(2)m=12,n=14,x=25｡此题虽然条件不完备,解之有困难,但它提供给兴趣爱好者一个广阔的思维空间,使每一位解题的人都以自己的数学背景和理解角度出发,获得对问题的解答.

2.2结论开放型

即在给定条件下,结论不唯一或不确定｡

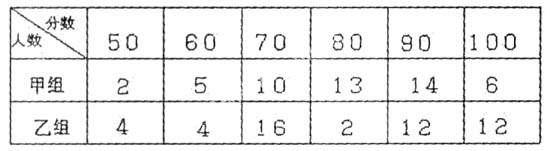
如:(统计开放型)

一次科技知识竞赛中,两组学生成绩统计如下:

已经计算两组的人均分都是80分,请你根据所学过的统计知识,进一步判断这两组竞赛中成绩谁优谁次,并说明理由｡

评析:这道题新颖别致,结论具有开放性,正确答案必须抓住“根据所学过的统计知识”,从众数､中位数､方差､高分等几个角度去进行必要的计算､评估,从而判断说明成绩谁优谁次｡①从众数看,甲90分,乙70分,甲组成绩较好;②从方差看,可求得S²甲 =172 ,S²乙=256 , S²甲2