江苏省南京市板桥中学(210039) 纪明亮

函数不等式恒成立问题是高考的重点考查内容,这类问题中含参数的题型在高考中出现频率很高,且难度较大,因为它涉及到的知识面广、综合性强.解决不等式恒成立问题的关键是等价转化,利用化归思想将不等式恒成立问题等价转化为函数最值的问题,从而使恒成立问题具体化.那么,如何等价转化? 有哪些方法? 2020 年高考新课标I 卷21 题(2)问就是一道经典的含参不等式恒成立问题,本文对这道高考题做了进一步研究,并将得到的结论与大家分享.

一、题目简析

题目(2020 年高考新课标I 卷第21 题(2)问)已知函数f(x)=aex−1−lnx+lna.若f(x)≥1,求a的取值范围.

分析 该题是不等式恒成立条件下求参数范围,解决这类问题原理是利用转化思想将其转化为函数的最值问题或值域问题来求解,在转化途径上,可采用“恒等变形构造辅助函数法”或“分离参数法”,一般地含参数问题中参数仅仅作为系数,而本题含参数的性质不同,参数不仅作系数还作为其中对数项的真数,直接分离参数就变得困难,那么构造函数在这道题中运用空间较大,下面就从不同角度构造函数对这道题进行解法探究.

二、问题解答

策略一 借助零点构造函数

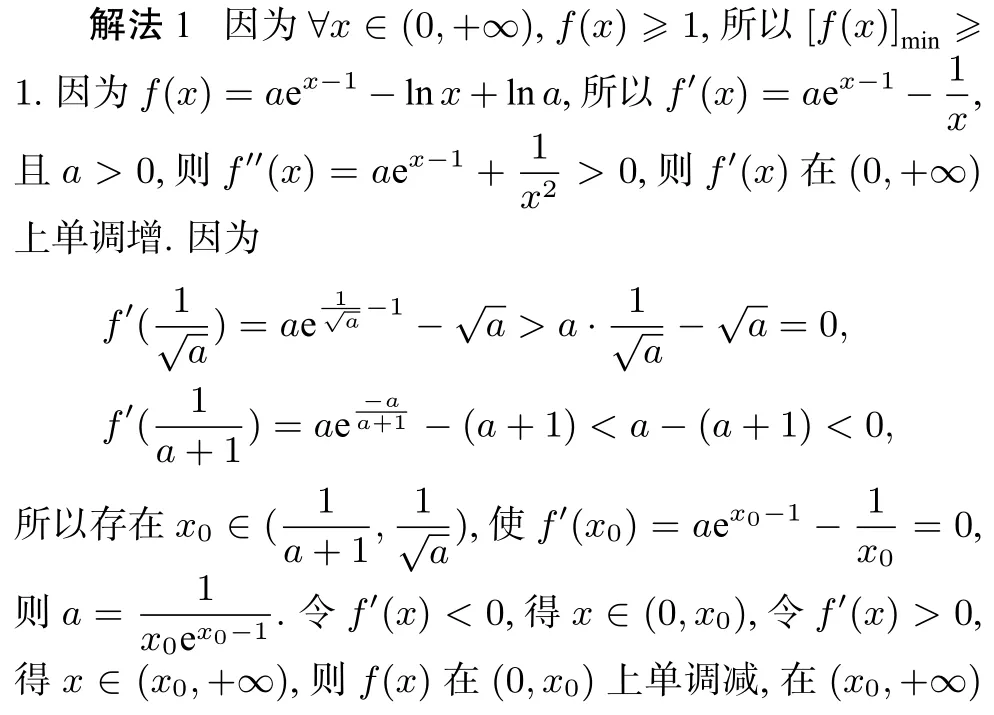
评析 本解法根据零点存在性定理,得出f′(x)存在唯一零点x0,根据f′(x0)=0 建立参数a与零点x0的关系,代入[f(x)]min=f(x0) ≥1,消去参数a得到关于x0不等式,并构造函数g(x),利用g(x)求出x0的范围.再根据a与x0的关系得到函数,根据该单调性求出a的范围.本解法巧设隐零点构造函数较为巧妙.

解法2 因为∀x ∈(0,+∞),f(x)=aex−1−lnx+lna≥1, 所 以∀x ∈(0,+∞),a≥ e1−x(lnx −lna+ 1), 则∀x ∈(0,+∞),e1−x(lnx −lna+1)−a≤0.

评析 题中f(x) 含有ex−1, 由于指数函数y= ex的n阶导数为y(n)= ex, 故可通过恒等变形构造g(x) = e1−x(lnx −lna+1)−a, 这样求导之后便于求出零点.根据h(x0) = 0 得到参数a与零点x0的关系, 代入[g(x)]max=g(x0)≤0,消去参数a得到关于x0不等式,并构造函数g(x),利用g(x)求出x0的范围.再根据a与x0的关系得到函数,根据该单调性求出a的范围.

策略二 统一参数形式构造函数

解法3 因为∀x ∈(0,+∞),f(x)=aex−1−lnx+lna≥1,所以∀x ∈(0,+∞),elna+x−1−lnx+lna −1 ≥0.

评析 因为

将a形式统一为lna, 并统一变量设t= lna −1,g(x) =ex+t −lnx+t.根据g′(x0) = 0 建立t与零点x0的关系t=−x0−lnx0,代入[g(x)]min=g(x0) ≥0 消去参数a得到关于零点x0的函数不等式,求得x0∈(0,1],再构造函数φ(x)利用其在(0,1]上单调性得t范围,进而得到a的范围.

策略三 根据同构关系构造外部函数

解法5 因为∀x ∈(0,+∞),f(x) =aex−1−lnx+lna≥1, 所以∀x ∈(0,+∞), elna+x−1+ lna+x −1 ≥x+lnx= elnx+lnx.设g(x) = ex+x,则∀x ∈(0,+∞),g(lna+x −1)≥g(lnx).因为g′(x)=ex+1＞0,所以g(x)在R 上单调递增,则∀x ∈(0,+∞),lna+x −1 ≥lnx,则∀x ∈(0,+∞),lna≥lnx −x+1.设h(x) = lnx −x+1,则lna≥[h(x)]max.因为所以令h′(x)＞0,得0＜x ＜1, 令h′(x)＜0, 得x ＞1, 则h(x)在(0,1)上单调增, 在(1,+∞) 上单调减, 则[h(x)]max=h(1) = 0, 则lna≥0,则a ∈[1,+∞).

评析 对aex−1−lnx+lna≥1 中指数项对数项分开得aex−1+ lna −1 ≥ lnx, 对a统一形式为lna, 得ex+lna−1+lna−1 ≥lnx,两边各加x得elna+x−1+lna+x−1 ≥x+lnx,变形得同构式elna+x−1+lna+x−1 ≥elnx+lnx,可构造外部函数g(x) = ex+x.本题还可变形成同构式elna+x−1+ ln elna+x−1≥x+ lnx, 再构造外部函数g(x) =x+lnx.借助外部函数单调性建立参数a与变量x的关系.外部函数具有降阶的作用.

三、感悟

关注函数形式,单调性和零点,函数形式指的是函数由哪些初等函数复合而成及各部分间的关联.这道题参数不易分离,且为隐零点问题,可以巧设零点,借助导函数建立参数与零点的关系,再进一步构造函数求参数范围,从解法一到解法四均采取这种策略.解法5 能敏锐的捕捉到函数不等式中的同构关系,构造外部函数,对函数降阶,求出参数范围.

构造函数时要充分结合初等函数的导数特点,构造出的函数要易于判断单调性和零点,比如lnx+ex≥f(x)(f(x)含参数),可根据解法2 对指数函数的处理方法将其变形为1 ≥[f(x)−lnx]e−x,再令g(x)=[f(x)−lnx]e−x,