磁-热-弹多物理场耦合波的反射和透射
2024-02-28岳田田王红韩旸杨雅琴李晓红周杨窦红双
岳田田,王红,韩旸,杨雅琴,李晓红,周杨,窦红双
磁-热-弹多物理场耦合波的反射和透射
岳田田,王红,韩旸,杨雅琴,李晓红,周杨,窦红双
(齐齐哈尔大学 理学院,黑龙江 齐齐哈尔 161006)
应用麦克斯韦电磁学理论引入洛伦兹力,反映外磁场对弹性波传播的影响.通过应用广义热弹性GN(Ⅱ)模型,反映热力耦合效应对弹性波传播的影响.通过色散方程和相速度,分析了外磁场和热力耦合效应对波动模式和色散特性的影响.应用连续性边界条件,计算出各种反射波和透射波与入射波的能流比,通过法向能量守恒验证了数值计算结果的可靠性.
耦合效应;洛伦兹力;反射;透射;能流比
以上文献没有揭示在外磁场作用下热-力耦合波的色散特性以及外加磁场对热弹性波反射和透射的影响.本文应用广义热弹性GN(Ⅱ)模型建模弹性固体中的热效应,通过应用麦克斯韦方程组,引入洛伦兹力,研究外磁场对弹性波传播的影响.首先,计算出磁-热-弹耦合波的色散关系,然后,计算耦合纵波入射时各种反射波和透射波与入射波的能流比,最后,通过法向能量守恒,验证数值计算结果的可靠性.
1 磁-热-弹耦合波的色散方程
广义热弹性GN(Ⅱ)模型为[7]200
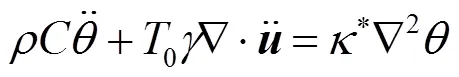
在均匀且完全导电的弹性固体中,电磁场由麦克斯韦方程组表示为
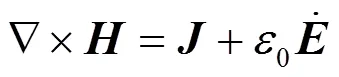
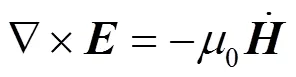
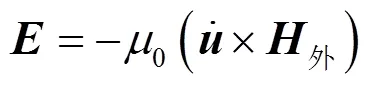
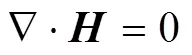
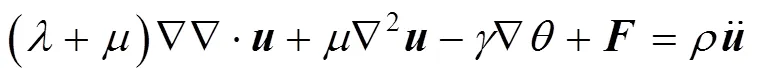
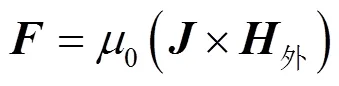
根据式(2)~(5),可以得到
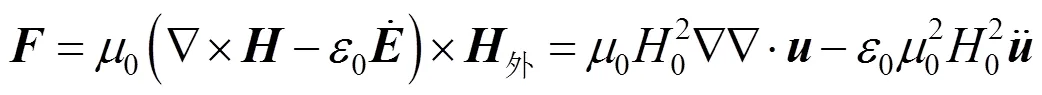
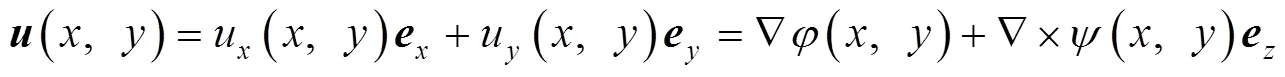
将式(8)(9)代入式(6)中,得到
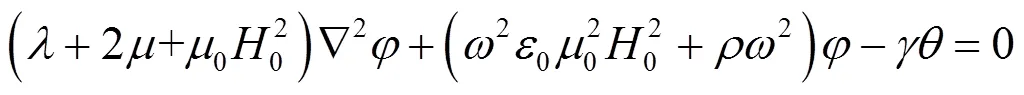
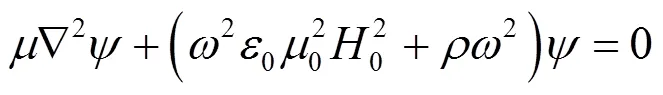
由式(10)(11)可以看出,热效应只影响P波,不影响SV波,而磁效应既影响P波也影响SV波,但是磁效应对P波和SV波的影响效果不同.
将式(1)(10)联立,可得
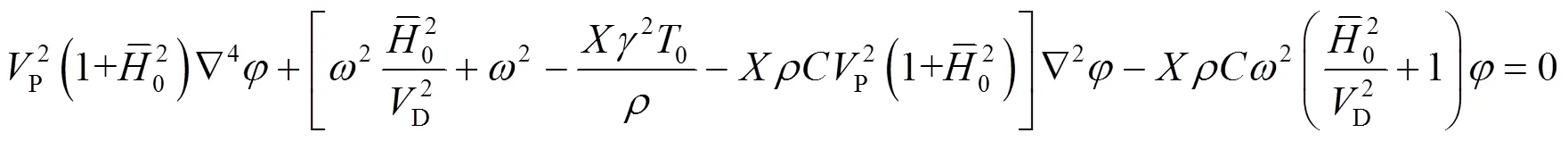
设式(12)的解具有如下形式
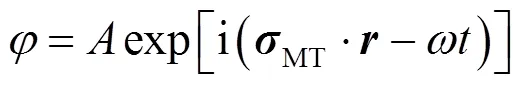
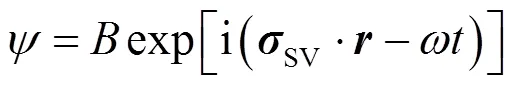
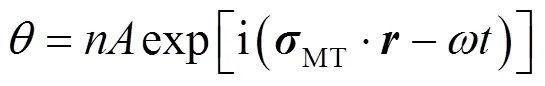
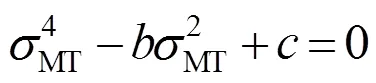
通过式(16)可以计算出
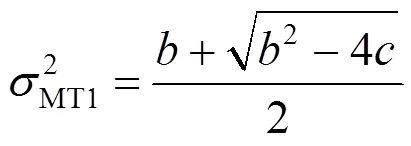
由式(17)可以看出,目前的模型中存在两个纵波,分别记为MT1波和MT2波.
将式(15)代入到式(1)中,可以推导出机械波和热波的耦合系数
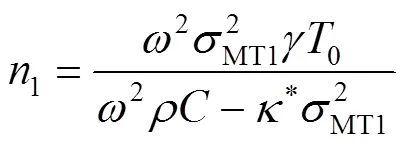
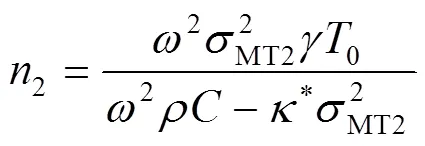
将式(14)代入到式(11)中,可以推导出SV波的解为
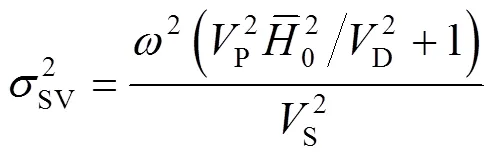
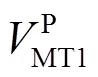
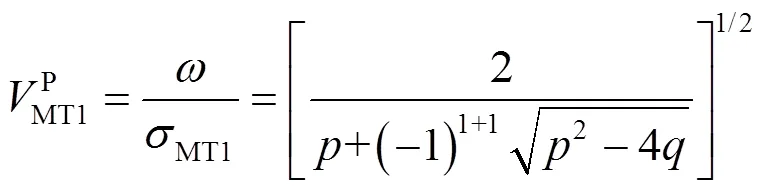
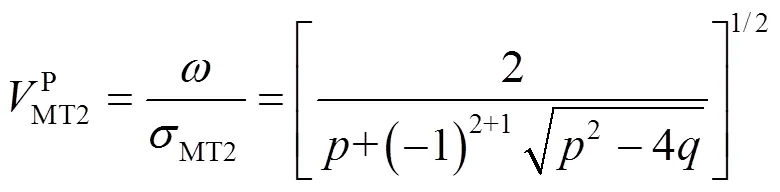
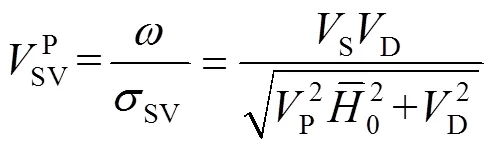
由式(21)~(23)可以看出,外磁场作用下的热-力耦合波是非色散波,外磁场和热效应只改变弹性波传播速度的大小,不改变弹性波的色散特征.
2 磁-热-弹耦合波的反射与透射
两种不同磁热弹性固体界面上弹性波的反射和透射见图1.
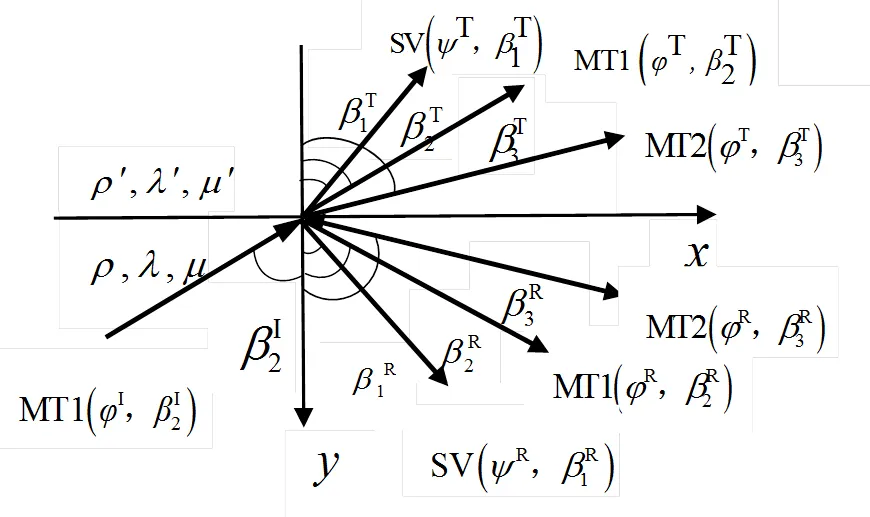
图1 两种不同磁热弹性固体界面上弹性波的反射和透射
根据Snell定理,在反射和透射问题中,所有波(入射波和反射波)的视波数都应相等,即
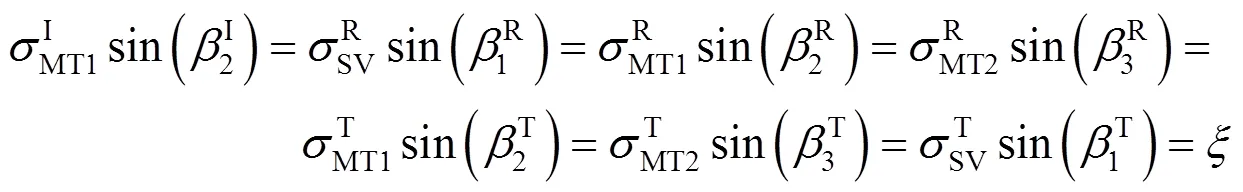
设入射波的势函数分别为
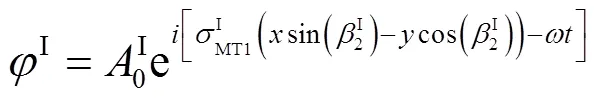
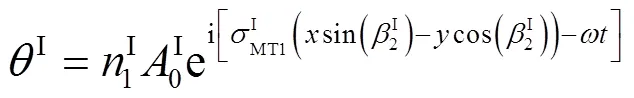
反射波势函数分别为
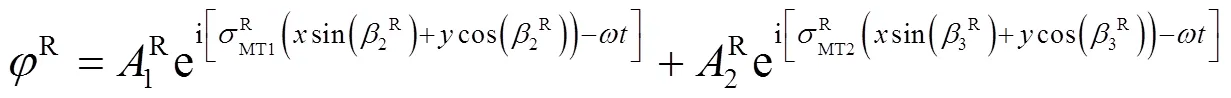
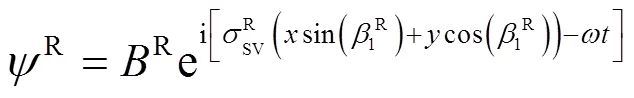
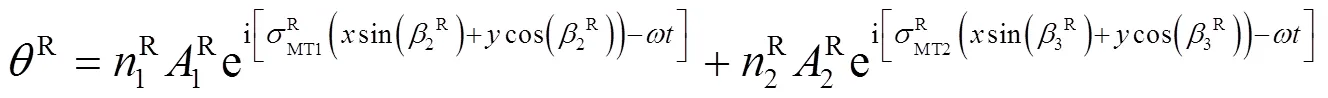
透射波的势函数分别为
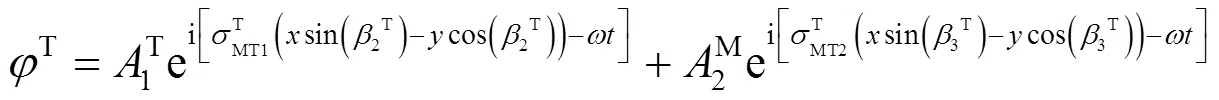
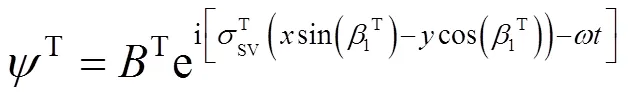
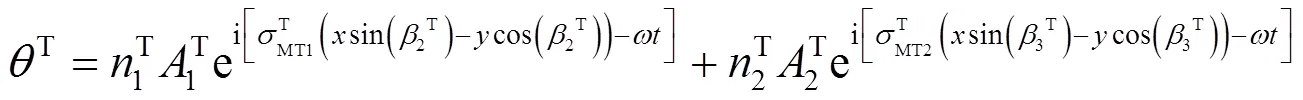
边界条件可以写为
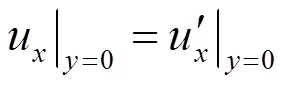
将式(25)(26)和式(27)~(32)分别代入式(33)中,可得到反射波和透射波与入射波的振幅比.
用在一个周期内反射波和透射波所携带的平均能流与入射波的平均能流密度之比来定义反射系数和透射系数.
计算一个周期内反射波、透射波以及入射波的平均能流.应用平均能流密度计算式
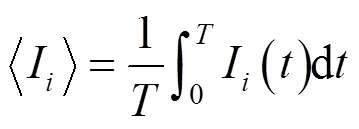
可以计算出耦合P波和耦合SV波的平均能流密度,即
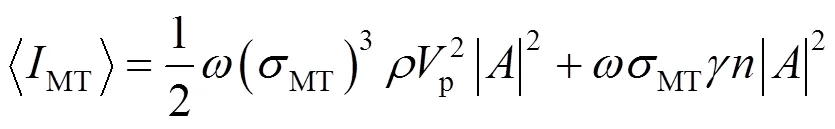
根据法向能量守恒原理,则当MT1波入射时,有
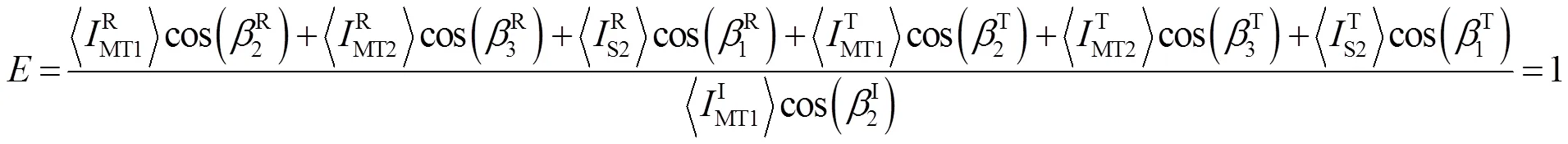
即入射波MT1在界面处通过单位面积的平均能流密度(输入能流)等于反射波和透射波在界面处通过同一面积的平均能流密度(输出能流).本文用式(36)对数值结果进行验证.
3 数值分析与讨论
取不同的外加磁场,考察MT1波入射时外加磁场对各种波的影响,结果见图2.
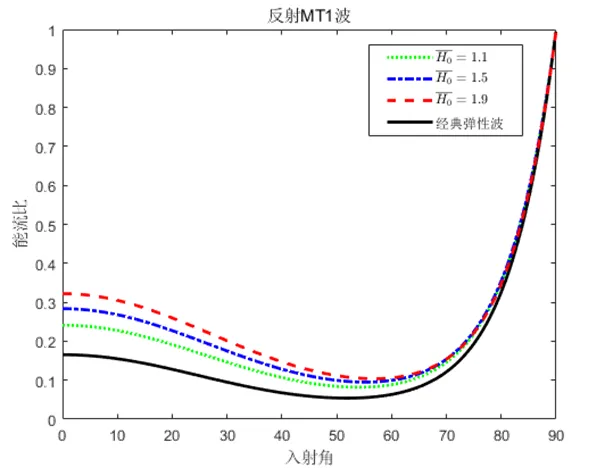
a 反射MT1波 b 反射MT2波 c 反射SV波
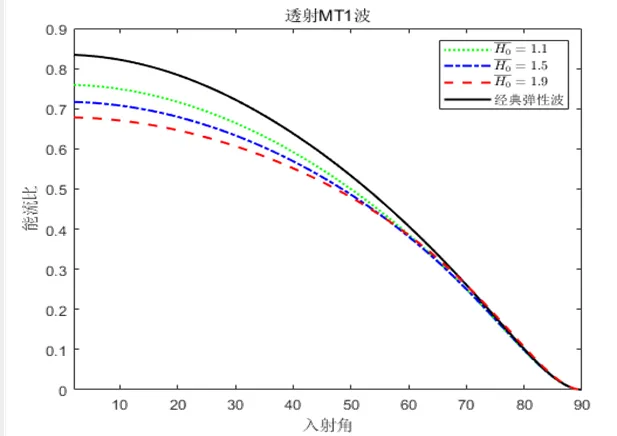
d 透射MT1波 e 透射MT2波 f 透射SV波
图2 MTI波入射时外加磁场对各种波的影响
由图2可以看出,反射MT1波、反射MT2波、反射SV波和透射MT2波随外磁场的增加而增加(见图2a~c和图2e);透射MT1波和透射SV波随外磁场的增加而减小(见图2d和图2f).反射MT1波和透射MT1波、反射SV波和透射SV波随外磁场的减小而逐渐趋于经典弹性固体中的弹性波.
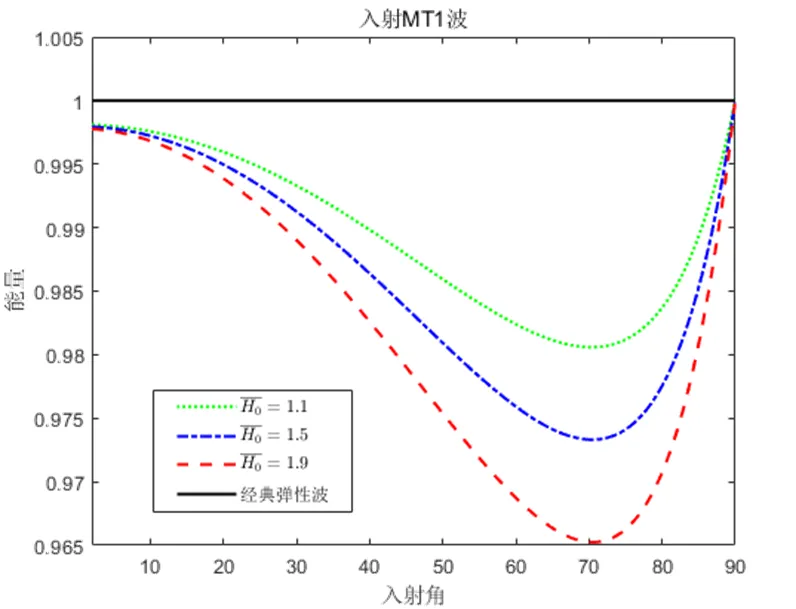
图3 能量守恒验证
能量守恒要求在界面处单位面积上流入的总能量等于在界面处相同面积上流出的总能量.本文对入射波、反射波和透射波所携带的一个周期内的平均能流密度进行了数值计算,并对能量守恒进行了验证.取不同的外磁场的值,考察入射MT1波的能量变化,结果见图3.由图3可以看出,数值计算的最大误差不超过5%,所以计算结果是可靠的.
4 结论
本文通过考虑外磁场对弹性波的扰动作用和固体中的热效应,研究了弹性波的反射和透射问题.通过数值计算可以得出结论:(1)无能量耗散的GN(Ⅱ)模型中的热传导方程是波动方程,而且热力完全耦合导致新的波动模式的出现;(2)热效应只影响纵波,对SV波没有任何影响;(3)外磁场对纵波和SV波都有影响,而且影响效果不同,但是外磁场不会产生新的波动模式;(4)GN(Ⅱ)热力耦合效应和外磁场都不改变弹性波的色散特征,只改变弹性波的传播速度的大小,即纵波和SV波仍然是非色散波;(5)外磁场的增加导致所有的反射波和透射MT2波增加而透射MT1和SV波减小,反射和透射MT1波和SV波都随着外磁场的减小逐渐趋近于经典弹性波.
[1] Kumar S,Pal C P,Majhi S.Reflection and Transmission of Plane SH-Waves Through an Anisotropic Magnetoelastic Layer Sandwiched Between Two Semi-Infinite Inhomogeneous Viscoelastic Half-Spaces[J]. Pure and Applied Geophysics, 2015, 172(10):2621-2634.
[2] Kumar S,Majhi S,Pal C P.Reflection and transmission of plane SH-waves in two semi-infinite anisotropic magnetoelastic media[J].Meccanica,2015,50(9):2431-2440.
[3] LI Yueqiu,BIAN Xinyu,WANG Changda,et al.The influences of external magnetic field on the reflection and transmission waves at the interface of two dipolar gradient elastic solids[J].Applied Mathematical Modelling,2023,121:524-541.
[4] Green A E.Thermoelasticity[J].Journal of Elasticity,1972,2:1-7.
[5] Green A E,Naghdi P M.On Thermodynamics and the Nature of the Second Law[J].Proceedings of the Royal Society A Mathematical Physical and Engineering Sciences,1977,357:253-270.
[6] Lord H W,Shulman Y.A generalized dynamical theory of thermoelasticity[J].Journal of Mechanics Physics of Solids,1967,15:299-309.
[7] Green A E,Naghdi P M.Thermoelasticity without energy dissipation[J].Elast,1993,31(3):189-208.
[8] LI Yueqiu,LI Long,WEI Peijun.Reflection and refraction of thermoelastic waves at an interface of two couple-stress solids based on Lord-Shulman thermoelastictheory[J].Applied Mathematical Modelling,2018,55:536-550.
[9] LI Yueqiu,WANG Wanli,WEI Peijun,et al.Reflection and transmission of elastic waves at an interface with consideration of couple stress and thermal wave effects[J].Meccanica,2018,53(11/12):2921-2938.
[10] LI Yueqiu,WEI Peijun.Reflection and transmission of thermo-elastic waves without energy dissipation at the interface of two dipolar gradient elastic solids[J].Journal of the Acoustical Society of America,2018,143(1):550-562.
[11] Das P,Kanoria M.Magneto-thermo-elastic waves in an infinite perfectly conducting elastic solid with energy dissipation[J].Applied Mathematics and Mechanics(English Edition),2009,30(2):221-228.
[12] 魏培君.弹性波理论[M].北京:北京科学出版社,2021.
ChinaReflection and transmission of magneto-thermo-elastic multi-physics fieldcoupling waves
YUE Tiantian,WANG Hong,HAN Yang,YANG Yaqin,LI Xiaohong,ZHOU Yang,DOU Hongshuang
(School of Science,Qiqihar University,Qiqihar 161006,China)
Lorentz force is introduced by Maxwell electromagnetism theory to reflect the influence of external magnetic field on elastic wave propagation.The generalized thermo-elastic GN(Ⅱ) model is applied to reflect the influence of thermo-mechanical coupling effect on elastic wave propagation.The influence of external magnetic field and thermo-mechanical coupling effect on the wave mode and dispersion characteristics is analyzed by the dispersion equation and the phase velocity.The energy flux ratios of various reflected waves and transmitted waves to incident waves are calculated by using the continuous boundary conditions.Finally,the reliability of the numerical calculation results is verified by the normal energy conservation.
coupling effect;Lorentz force; reflection;transmission;energy flux ratio
O241.8∶O441
A
10.3969/j.issn.1007-9831.2024.02.003
1007-9831(2024)02-0009-06
2023-07-03
黑龙江省基本业务费专项资助项目(135509123);黑龙江省高等教育教学改革项目(SJGY20210966);齐齐哈尔大学教育科学研究项目(GJZRZX202003)
岳田田(1998-),女,黑龙江绥化人,在读硕士研究生,从事复杂介质弹性波传播研究.E-mail:2095246045@qq.com
王红(1971-),女,黑龙江齐齐哈尔人,教授,从事复杂介质弹性波传播研究.E-mail:wanghonglaoshi@163.com.
