华好，李飚

很多人至今还记得一篇关于“烧水泡茶”的统筹方法科普文章。统筹方法来源于“运筹学”（operational research），可以用来合理安排工序提高效率，也可以用来求解空间问题从而为建筑设计服务。现代运筹学起源于第二次世界大战。英国军方用数学规划来制定飞机、轮船的出行计划、最合理地调配物资。前苏联数学家坎托罗维奇在调配工厂产能的工作中建立了线性规划（linear programming）方法[1]，之后凭此获得了诺贝尔经济学奖。二战后，线性规划逐渐在民用领域发挥核心作用。丹齐格（George Dantzig）发明的单纯形法沿用至今，而冯·诺伊曼（John von Neumann）发现了对偶原理[1]。1960 年代末，科学家借助计算机开始尝试利用线性规划来解决空间布局问题[2]。这种单纯追求经济性与效率的方法很适合工业厂房，但长期以来并未得到建筑师们的青眯。

从建筑学的立场出发，计算机辅助建筑设计之父米歇尔（William Mitchell）、《进化建筑》的作者弗雷泽（John Frazer）代表了数字建筑的先驱。但直到21 世纪的运算化设计（computational design）兴起才较为全面地实现了建筑平面布局的自动生成，真正帮助建筑师拓展了建筑设计的可能性。优化算法（包括线性规划）、参数化（包括形状语法）、多智能体系统代表了平面布局“程序化”的几大类理论方法。贝尔拉格建筑学院彼得·特鲁默（Peter Trummer）团队将生成逻辑贯彻到聚落、组团、建筑单体、室内多个层面[3]。苏黎世联邦理工学院卢德格尔·霍夫施塔特（Ludger Hovestadt）团队将多智能体系统与优化算法相结合进行了大量设计实践[4]。国内高校紧随其后进行了大量研究。清华大学徐卫国与黄蔚欣团队拓展了多智能体系统的生形方法[5]，同济大学孙澄宇团队开发了面向实践的城市三维模型布局生成方法[6]，南京大学吉国华团队基于参数化模型研发了性能优化算法[7]，东南大学李飚团队通过算法模型解析设计逻辑进而推动设计创新[8]。

“古老”的数学规划方法在建筑设计中的应用也突飞猛进。其中一个因素是各种数学规划软件如Gurobi、IBM 旗下的CPLEX 日益成熟。整数规划（integer programming）在建筑设计应用中有了重大突破。本文结合国内外最新研究进展与本研究团队在2018-2022 年期间完成的生成设计实验，指出线性整数规划模型能够综合性地处理房间、走道、房屋间距、路网等问题[9-10]，涉及建筑设计与城市设计[11]。如今，建筑师可以运用这些运算化工具来辅助设计或者直接生成方案，促进了建筑学与运筹学之间的跨学科合作。

本文第1、2 节诠释了线性规划的基本原理以及在建筑设计中的早期应用历程，并指出其局限性。第3 节基于前人的技术积累以及本团队在近5 年内的设计研究，提炼了3 类典型建筑设计问题（路径规划、场地内建筑布局、建筑平面生成）与线性整数规划模型之间的对应关系，从而把运筹学技术方法与多种建筑设计场景结合起来。

1 线性规划的基本原理

线性规划是运筹学和最优化理论的重要基石，是计算机科学、工程领域、经济与管理科学重要的数学工具。典型的线性规划有3 个要素：（1）多个决策变量（variables），通常为一组整数或小数；（2）一个线性的目标函数（objective function），即关于变量的一个线性函数；（3）多个线性约束条件（constraints），即关于变量的多个等式或不等式。

一个实际问题转化为3 个要素之后就可以用标准的程序来获取最优解（得出每个变量的值）。运筹学致力于寻找更好的求解方法或问题表示方法。如今，在商业化求解器中输入变量、目标函数和约束条件，求解器就能给出最优解。而建筑师的挑战在于如何将设计问题转化为这些抽象的数学要素。

整数规划只使用整数变量，而0-1 整数规划只允许0 或1 作为变量[12]。假设有3 个房间的长宽如图1 所示，如何选取其中几个房间使其宽度总和最大但又不超过6m？我们可以设变量x1，如果值为0 表示不选取1 号房间，值为1 则表示选取1 号房间。用同样的方式设x2、x3变量，由此定义约束条件：

1 水平排布3个房间

并设立目标函数：

希望得到它的最大值。不难看出，最优解为x1=1,x2=0,x3=1。而0-1 整数规划的魅力在于它能很方便地表示“或” “且” “如果……那么……”等逻辑关系。如果这个排房间的游戏允许旋转房间（但每个房间最多只能被选用一次），就需要增加6 个0-1 变量：u1表示是否采用1 号房间的短边，v1表示是否采用长边。用类似的方式定义u2，v2，u3，v3，约束条件就变成：

其中wi和hi分别表示i 号房间的长短边。第二组等式隐含了“选用长边或短边”选项。

这种线性规划方法可以应用到复杂的、大规模的建筑设计问题中。与工程领域相比，建筑师往往不追求唯一的“最优”解，更重视一系列各不相同的“较优”解以便继续深化或调整。而商业化求解器通常可以提供多个“较优”解。运筹学方法及其相关软件的实用性越来越强。虽然数学规划在建筑学中的运用比较滞后，但这种探索已持续了半个多世纪。

2 运筹学的建筑应用历程

2.1 早期探索

建筑空间的布局问题类似于经济学领域中的“资源的最佳布局”（optimum allocation of resources）问题。经过二战时期的初步探索，空间布局问题逐渐进入民用领域。1957 年科普曼（Tjalling Koopmans）等人量化了多个工厂之间的布局问题[13]，而工厂内部的平面布局问题在1960 年代受到了广泛的关注。阿莫（Gordon Armour）等人尝试在正交网格上排布各个生产部门以达到最少的资源消耗[14]，并采用了二次整数规划（quadratic integer programming）。

1968 年，路易斯安那州立大学的阿圭勒（Rodolfo Aguilar）团队第一次明确地用线性规划来解决建筑内部的布局问题[2]。但他们并不关注具体的空间形态，而是像开发商一样在给定的地块中策划每种功能的面积、出租与售卖的比例、功能的楼层分布等问题。该策划工具囊括了丰富的内容，包括市场需求、功能的楼层偏好、停车位、建设费用、建筑师设定的布局规则等等。

米歇尔（William Mitchell）在1975 年总结了当时最先进的建筑空间自动生成技术[15]，其中线性规划代表了一种高效的全局搜索方法。但他认为线性规划依然很难表达建筑平面，因此选用了动态规划（dynamic programming）来生成建筑平面，吉罗（John Gero）在此基础上做了更新[16]，能够处理每个房间的边长最大最小值、面积最大最小值、最大长宽比。

2.2 线性与非线性

为了弥补线性规划在建模中的局限性，非线性规划（nonlinear programming）、动态规划、混合整数规划（mixed-integer programming）在1980 年代之后被广泛运用。新的高效算法被编写成求解器（计算机程序）。各种数学规划方法与建筑设计的结合逐渐变得多样化。

大阪大学的吉田教授（Katsuyuki Yoshida）用非线性规划来生成最优化的住宅平面[17]。他按一定的规则将一个长方体分割成多个房间，而非线性规划用来优化分割过程中的具体参数。目标与限制条件包括：每个房间的长宽高、房间朝向、围合体的造价、檐下空间、房间之间的相邻关系等。

另一种策略是将每个房间看作是可以浮动的长方形。每个长方形的位置由两个小数变量（x,y 坐标）来表示。长方形之间不能重叠，但要求相邻的房间（长方形）靠在一起。来自麦加大学的研究人员在1980 年代末尝试用非线性规划来优化这种浮动式的空间布局[18]。之后香港理工大学设计学院完善了该类生成方法[19]。

房间的浮动也可以在正交网格上进行，此时每个长方形的x、y 坐标，以及长与宽都由整数来表示。泰国的研究人员采用混合整数规划在网格上实现了建筑平面的生成[20]。他们基于GLPK 求解器开发了一款图形化的程序，建筑师可以方便地输入每个房间的尺寸、拓扑关系等设计条件。程序输出最优化的结果，并导出DXF 矢量文件。

2.3 回归建筑

经过1960-1970 年代的理论与技术奠基，到1980 年代之后技术与方法多样化发展，整数规划方法在近10 年里重新聚焦于城市设计、建筑、室内3 个空间尺度中的具体问题。其方法主要包括：（1）在空间上，把多样化的空间形态转化为可以被整数表示的离散状态；（2）对于设计目标与约束条件，把各类逻辑关系转化为整数线性表达式。

针对地块内部的交通网络，亚利桑那州立大学开发的整数规划工具使设计师能够设定路网覆盖密度并控制路网等级[9]，该工具也能在变形网格上生成建筑平面[10]。如图2 所示，定义7种房间模板和走廊模板、电梯井模板之后，整数规划算法可以在复杂的网格中排布房间，确保连通性和各种房间数量之间的比例。

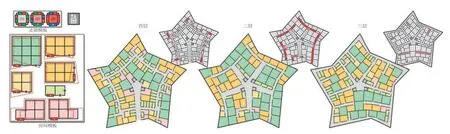
2 不规格网格上的建筑平面布局，引自参考文献 [10]

东南大学团队攻克了网格上的日照强排问题[11]：使住区的容积率最大化的同时满足南向房间的日照需求。0-1 整数规划既可以表达多层建筑的日照间距，又可以处理高层建筑每个时刻的投影（图3）。覆盖路网（coverage network）算法也得到了改进，解决了道路曲直、死胡同等问题。

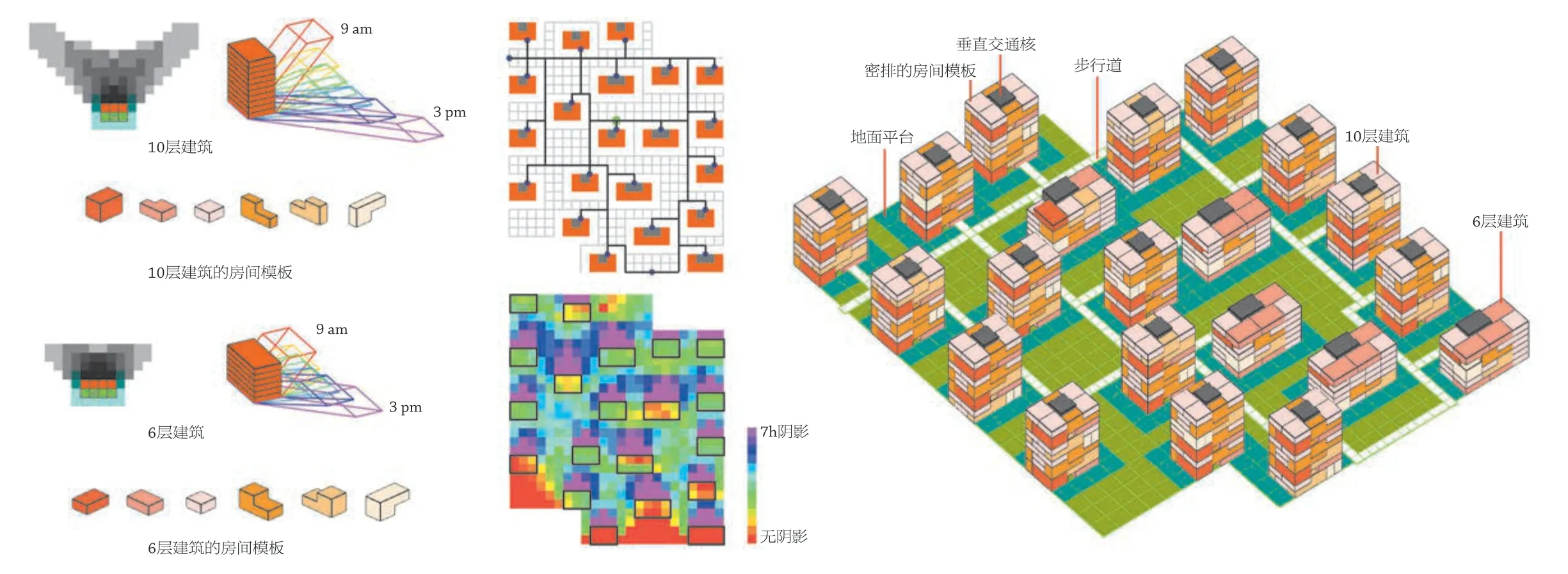
3 高层住区规划，引自参考文献 [11]

中国科学技术大学利用混合整数二次规划（mixed integer quadratic programming）开发了较为完善的建筑生成程序[21]。程序可以处理L 形等复杂形状的房间，并在生成住宅方案的过程中考虑上下层对齐的问题（图4a），可以处理规模比较大的公共建筑（图4b）。

4 建筑平面布局，引自参考文献[21]

3 建筑空间的生成

用线性表达式来描述复杂多变的建筑空间是一项长期挑战。本节基于近年来国内外的学术前沿与本团队的实验总结，提炼出用0-1 整数规划来描述设计对象并生成设计方案的方法：

（1）路径规划：利用“水流”概念对路径的连续性、覆盖范围、曲折度进行建模，可以把路径规则涉及的图（graph）问题转为线性整数表达式；（2）地块内的建筑布局：在网格上对建筑的二维形状模板进行各种拓展，实现相邻、日照遮挡等复杂关系的线性描述；（3）建筑平面生成：在网格上利用建筑的二维形状模板，将满铺、相邻、旋转问题转化为线性整数表达式。

3.1 路径规划

城市道路、小区内部道路、车行道、人行路径等均有各自的设计要点，其中有两类路径规划模型受到了广泛关注：（1）斯坦纳树（Steiner tree），即以最短的总路径连接地块上的所有目标点；（2）覆盖网络（coverage network），即以最短的总路径平均地覆盖整个地块，覆盖半径可以调节[9,11]。我们可以把两种网络模型都想象为：有水流从源点出发，流向各个目标点。斯坦纳树适用于目标点已事先确定的情况，覆盖网络适用于目标点不确定的情况。“水流”概念可以反映路径的全局联通性，避免出现道路孤岛。

两种路径模型都用一个0-1变量xij来表示网格中的某一条边（连接两个节点）是否属于路径，并用两个0-1 变量yij和yji分别表示是否有“水流”从点i 流向点j、从点j 流向点i。对每一条边建立等式：

它有两个作用：（1）保证最多只能有一个方向的“水流”通过一条边，即yij和yji不能同时为1；（2）如果有“水流”从任一方向通过一条边，这条边就属于路径，即让xij的值为1。

在此基础上，斯坦纳树在确保全局“水流”联通的情况下使路径的总长度最小[22]。斯坦纳树有一个显著的特点：路径中不存在环路，即每个目标点都是死胡同，这对道路规划往往是不利的。如果要形成回路，可以点对点地加入最短路径或是同时生成两组斯坦纳树来构成环路[11]。

覆盖网络在“水流”联通、覆盖半径的约束条件下使路径最小化。路径的覆盖距离可以预先设定。图5 显示了覆盖距离分别为0、1、2 的情况下生成的路网，其中第一行的3 组方案不考虑路径的曲直，而第二行的3 组方案尽量让道路笔直1）。

5 覆盖网络的曲直与覆盖距离

3.2 地块内的建筑布局

在地块中合理地进行建筑布局涉及城市设计问题与建筑设计问题。建筑布局需考虑法律法规、自然条件、开发需求、建筑形体等因素，而本小节介绍两类问题：（1）强排：在满足日照条件的情况下尽量提高容积率；（2）韵律：使建筑体量在宏观布局中体现出一定的空间韵律。强排是一个可以量化的科学问题，而韵律与设计手法相关。

建筑布局首先要处理两个最基础的几何问题：建筑之间不重叠、每个建筑都在地块内。首先将给定的建筑轮廓设为固定的模板，如图6 所示，一个T 形建筑表示为4 个方格的集合A(i,j)={(i,j),(i-1,j+1),(i-1,j),(i-1,j-1)}，圆括号中的两个数字表示行与列1）。如图6，地块的可建设范围在网格中由白色方格（对应集合P）表示，地块的外边界由灰色方格（对应集合Q）表示。可建设范围内的每个格子(i,j)都关联一个0-1 变量xij，表示这个格子上是否要放置一个建筑模板A 的参考点（如图6 中，每个模板的参考点用白色小圆圈表示）。

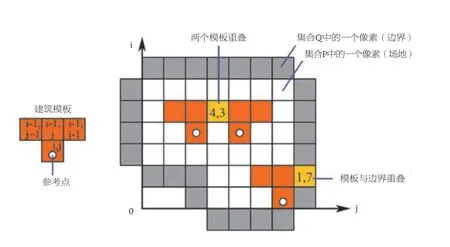
6 建筑模板与地块的关系

把建筑放置在可建设范围内的约束条件为：

即任一建筑模板都不能和灰色外边界重叠。图6 中的（1,7）位置属于地块外边界，但被一个模板覆盖了。因此这是一个不合法的状态，此处的值违反了条件（1）：

建筑之间互不重叠的约束条件为：

图6 中的（4,3）位置有建筑重叠的情况，此处的值违反了条件（2）：

这两类基本条件可以扩展到多种建筑模板。此外，每一种建筑模板可包含多个层：建筑轮廓、室外场地、建筑的阴影等。以住区的建筑布局为例，日照条件是一个关键控制因素。对于6 层以下的多层住宅，我们可以将建筑的阴影表示为建筑模板的一部分，禁止南向房间与其他建筑模板的阴影区域重叠。对于多层住宅，需要分别计算每个时刻的建筑阴影，限制南向房间的最大被遮挡时长。图3 显示了一个基于高层日照条件的强排结果。

城市中建筑布局的对称性对构建城市肌理、营造场所感、引导公共活动具有重要作用。几何对称性可以通过移动、旋转、反射等操作来完成。0-1 整数规划可以处理移动对称性（translational symmetry），比如用SOS2 约束条件来定义两个模板如何重叠[11]，从而创造建筑排布的韵律。

3.3 建筑平面生成

建筑内部的房间布局是建筑师的核心技能，也是线性规划的一个技术难点。房间布局通常要考虑以下几类问题：（1）每个房间的几何特征，如面积与长宽比；（2）房间之间的相邻关系，建筑师通常采用“泡泡图”来表示房间相邻关系；（3）建筑出入口、建筑轮廓的总长、房间的朝向、走廊的效率等条件。本小节重点讨论0-1 整数规划如何处理房间相邻关系以及房间的几何特征。

首先考虑一个简单情况：每个房间的模板是固定的、唯一的（方向确定，不能旋转）。如图7 中的两个房间模板A 与B，设0-1 变量xAij表示格子(i,j)上是否有模板A 的参考点，同理，0-1 变量xBij表示格子(i,j)上是否有模板B 的参考点。首先限定每种房间只能在网格中出现一次：

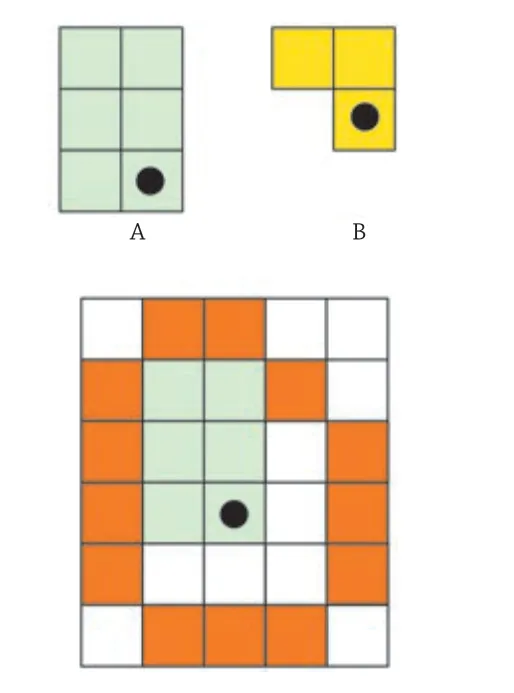
7 两个房间之间的相邻关系

任意一对房间之间的相邻关系可以很明确地表示。在图7 中可以看到：模板B 的参考点位置位于橙色方格上的时候，两个模板处在相邻的状态。橙色方格形成的集合C 可以表示成模板A 与B 的一个函数：

由此，两个房间相邻的约束条件变得十分简单：

基于房间拓扑关系的建筑生成也可以延伸到三维空间中[23]。东南大学“拼多多”设计研究项目在25,992m2的高层塔楼体积中设置了278 户公寓，可容纳510 余人，在户型、楼层平面、塔楼3 个尺度上进行居住元素的最优化拼接（图8），其中大型公共空间是跨楼层的[24]。

8 “拼多多”高层公寓楼设计

比较复杂情况的是，每个房间包含了多个模板。譬如，一个面积为6 个格子的房间可以采用2 ×3 或3 ×2 的长方形模块。此时，描述两个房间相邻状态要分类讨论两个房间采用了哪个模板，需采用“如果……那么……” 约束条件。主流求解器如CPLEX 与Gurobi 可采用指示约束（indicator constraints）表示这类条件，或者用big-M 方法将其转化为线性不等式[24]。

4 结语

计算机技术在建筑学领域引发了计算机辅助设计、运算化设计、多模态人工智能等一系列革命性的应用。运算化设计中的数学优化方法支持性能驱动的建筑空间排布，一方面可以推动设计创新，另一方面需要积极地转译传统设计思维。源于运筹学的数学规划方法是建筑运算化设计方法的古老分支，近十几年来又重新进入建筑师与学者的视野，并逐渐走向实用阶段。本文集中介绍了线性整数规划的建筑应用，而运筹学其他数学方法的应用尚待挖掘。运筹学与建筑学之间的跨学科发展正在为建筑师带来新的机遇与挑战。

本文梳理了线性整数规划原理及其建筑应用，提出了3 类对建筑设计适用性较广的模型：路径规划、地块内建筑排布、建筑平面。数学规划在建筑空间设计中的应用隐含了3个层次：（1）设计思路与数理逻辑之间的双向转化。数学规划依赖明确的数学表达式，如目标函数与约束条件。建筑师可以根据设计意图灵活运用数学规划模型，也可反过来根据数理逻辑来调整设计思路；（2）各类几何元素的设置，包括网格的选择（正交网格、三角网格、不规则网格）、建筑模板设计（可以影响建筑之间的相邻关系、对称性与韵律）等；（3）通过计算机编程与求解器来运行数学规划算法，得到大量优化方案，可作为深化设计或再研究的基础。

这三者在客观上是相互独立的，但在设计实践中需有机地结合起来。实际上，运筹学与建筑设计的融合依然处于迅速发展的起步阶段，我们需要在一个跨学科的语境中不断寻找数理逻辑与建筑空间之间的纽带。

注释

1）算法模型及详情参见参考文献[11]。