冯唐思捷 梁 伟

(北京航空航天大学航空科学与工程学院,北京 100191)

引言

随着计算机硬件的更新迭代,数值计算资源呈现了爆炸式增长的态势.快速降低的计算成本催生了一大批使用大数据进行计算的新型数值方法,例如人工神经网络和深度学习等技术已经在图像识别[1]和认知科学[2]等方面取得了突破性进展.但在工程和物理领域,这些新兴方法的应用推进并不顺利.其中一个重要的原因是这些领域的数据集的获取成本高,稀疏性和不确定性大,纯粹依靠数据驱动的方法效率低且精度不高.因此,大部分工程和物理问题采用的求解方法都是基于物理模型的正向求解算法.物理模型通常由偏微分方程组的形式刻画或者描述,例如Navier-Stokes[3]方程、Allen-Cahn[4]方程和Schrödinger[5]方程等.基于求解偏微分方程的传统求解方法虽然能够求解正向问题,但在相应的逆问题、高维问题和非线性问题上具有计算成本高,人机交互频繁,技术突破难度大的缺点.

近年,同时利用大量计算数据和物理规律来求解偏微分方程组所代表的物理模型成为了一个可能的工程技术突破口.一方面,在Cybenko[6]和Hornik[7]证明的神经网络万能逼近定理的前提下,拥有多于一个隐藏层的神经网络可以将任意从向量空间Rn到另一个向量空间 Rn进行投影的Borel 函数的拟合误差达到足够小.另一方面,得益于编程语言的发展,如今神经网络的主流搭建平台,例如Tensorflow 和Pytorch 等,都广泛使用自动微分 (auto-differentiation)[8]来自动计算点与点之间的多阶梯度.自动微分使得方程中的偏微分项可以融入到神经网络的损失函数设计当中.这样,物理模型中包含的物理知识作为一项信息输入到神经网络的优化过程中,有这项信息输入的神经网络就脱离了仅仅将输入输出数据进行匹配的纯数据驱动范畴.这样综合了数据驱动和物理信息两方面的神经网络被称之为物理信息神经网络(PINN).

PINN 最先由Raissi 等[9-10]于2017 年提出,并在2019 年证明对多种偏微分方程有效[11].PINN继承了深度神经网络(DNN)的函数逼近能力,其整体架构也与深度神经网络类似:采用前馈神经网络作为基本逼近单元,将函数的自变量作为输入,在输出层输出给定函数或给定方程的近似解.这种将偏微分方程中的信息内嵌到损失函数的做法使得损失函数在优化的过程中遵循了相关的物理定律.与传统算法相比,PINN 不仅不需要任何网格划分的前处理,也不需要遵循任何人为的先验假设[12-13].简洁的网络架构使得PINN 能够对大部分偏微分方程组进行有效求解,并可以有效攻克一些常规数值方法中的难点,例如维数灾难和逆问题求解中的参数识别等[14-19].

在弹性力学中,由于控制方程大多数为高阶偏微分方程,在复杂几何区域下求解困难.近年来,学界注意到PINN 的良好特性可用于求解固体力学中的一些实际问题并验证了其有效性.Tao 等[20]使用PINN 对薄壁圆筒壳在线性屈曲失稳下的相对于理论解的塌陷因数(knockdown factor)进行了研究.结果证明,PINN 可以在提供更少的标签数据的情况下得到与传统ANN 表现相似的神经网络,其预测值不高于标签数据中的实验数据,便于提供结构真实屈曲载荷的保守预测[20].Li 等[21]使用PINN 方法基于偏微分方程形式和Rayleigh-Ritz 能量条件构建损失函数求解了薄板的弯曲问题,结果和有限元方法的精度相仿.Haghighat 等[22]则在他们的研究中讨论了PINN 作为代理模型,利用等几何分析和有限元解作为标签数据来求解线弹性力学和弹塑性力学问题的可能性.Bastek 等[23]则研究了在非欧流型下求解基于Naghdi 板壳理论的变形问题,并讨论了待求解方程强弱形式对神经网络的影响.Yan 等[24]利用PINN 方法和极限学习机(extreme learning)研究了复合材料薄壁结构的静力和动力问题,并将神经网络解与这些问题的Navier解进行了对比.虽然PINN 在求解实际问题上仍然处于事实上的起步阶段,但其相对于传统数值方法拥有不可忽视的潜力.

工程实际中,薄壁结构在工作时主要受轴向压缩载荷,在这种载荷的作用下,结构容易发生屈曲失稳从而达不到预期的承载能力[25-26].薄壁结构的屈曲和后屈曲控制方程为复杂的非线性耦合方程,一般情况下难以得到显式表达的位移场理论解,而在数值方法中,也一般采用有限元方法进行求解其弱形式积分方程.之前列举的一些工作虽然对于固体力学中的偏微分方程求解提供了新的思路,但求解的力学问题多局限于线性理论,而对于非线性问题则鲜有涉猎.而屈曲问题是否考虑非线性效应将对结果产生很大的影响.由于无论求解手段如何,屈曲问题和后屈曲问题都可以转化为对其控制方程求拟合解,故而本文将结合物理信息神经网络对结构的非线性屈曲问题,基于求强形式控制方程的拟合解来发展新的解法.本文采用PINN 方法对典型薄壁板壳结构的屈曲和后屈曲问题进行研究,针对不同的边界条件和载荷形式进行结构屈曲载荷和屈曲平衡位移模态的研究.本文利用Lu 等[27]建立的开源Python 库DeepXDE 编写了3 种典型板壳结构的求解代码,实搭建的实验平台为Python 3.9.16,所有的神经网络运算均在GPU 上利用NVIDIA 公司开发的CUDA 运行.PINN 解在最后与有限元解进行了对比以验证本文方法的有效性.

1 薄板壳非线性屈曲控制方程

长宽均为a,厚度为h的方板,其弹性模量为E,材料泊松比为 ν,受面内载荷Px,Py,Pxy作用,引入Airy 应力函数F,将3 种面内载荷统一表示为F的偏导数,即

以W∗,W分别表示初始缺陷带来的挠度和因为载荷施加得到的中面挠度,中面x,y方向上的位移分别记为U,V.由von-Kármán Formulation,可知其几何方程为[28]

式中,上标0 代表中面的应变分量和曲率分量.以薄板中面为研究对象,其平衡方程可写为

假设材料为各向同性线弹性的,并考虑协调方程

以及物理方程

将中面位移全部使用挠度W∗,W和Airy 应力函数F表达,则可以得到以下的平板屈曲微分控制方程[29]

边界条件可分为3 类:简支、固支与自由,其对应的表达式分别为

简支

固支

自由边

为了减少神经网络需要拟合的边界条件,对于固支边和简支边的位移连续条件,可以在用对神经网络的拟合过程中使用硬边界约束(hard constraint).例如,若某一薄板为四边简支,则可以对神经网络所代表的非线性映射做变换,即令

这样非线性映射则可自动满足力学模型的位移边界条件.对于边界条件(8),需要融入到损失函数的边界条件减少了一项,其余的边界条件也可以构建类似的试函数来减少损失函数项数.

2 神经网络模型

2.1 网络框架

本文采用的PINN 神经网络结构如图1 所示.

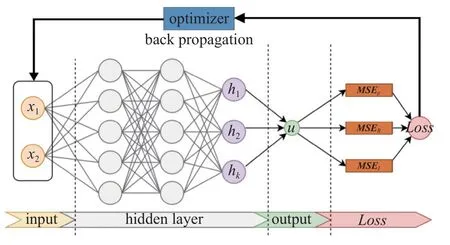
图1 PINN 求解网络框架图Fig.1 A framework of using PINN network as PDE solver

此全连接神经网络的基本参数为La×Nu,前者为隐藏层层数,后者为单个隐藏层神经元数.神经网络的输入为几何域坐标 (x,y),经过神经网络输出的拟合解为挠度与应力函数该问题所对应的非线性映射可以在数学上表示为

式中,参数Wi,bi分别为每一层神经元组成的权重矩阵和偏置向量,每一层的非线性激活函数由 σi表示,它们构成了需要训练的网络参数 Θ.

对于激活函数 σi,根据Jagtap 等[30]的工作,使用逐层自适应的激活函数(locally adaptive activation function,LAAF)可以进一步提高PINN 的表现.在第3 章的算例中,均采用文献[30]中的自适应激活函数,其在DEEPXDE 开源库中可通过命令LAAF调取,其基础的激活函数为sigmoid 函数,即

2.2 误差函数与算法流程

一般来说,PINN 的损失函数 Loss 由3 个部分组成.如果由均方误差(mean square error,MSE)来衡量神经网络的拟合误差,则3 个部分分别是代表偏微分控制方程的误差MSEP,边界条件误差MSEB,以及初值条件误差MSEI.PINN 方法的待优化损失函数Loss可以带权重的方式表示为

MSEP作为整个求解域上的控制方程的损失函数,其首先由神经网络在整个求解域上预先布置的采样点上得到预测挠度与应力函数再将预测解代入控制方程求出残差.设在域内总共布置了NP个采样点,即有

MSEB作为边界上的损失函数,其计算方法与MSEP相似.以四边简支的边界条件为例,由于已经在神经网络的输入端引入了变换层,位移的连续条件被满足,故只需要考虑弯矩条件

MSEI作为表示初值的误差,在屈曲方程中由于不含时,因此初值项为0.

确定PINN 需要优化的损失函数后,采用基于Python 的机器学习框架Tensorflow 中的基于计算图的自动微分(auto differentiation)就可以计算这些函数中微分项.

损失函数Loss的表达式中,[wP,wB,wI]分别为3 误差项对应的权重值向量.在实验中,作者发现可以将所有损失函数项的数量级调整至接近一致,这样做可以提高PINN 算法的训练精度,但具体权重仍然需要具体问题具体确定.一种办法是在确定随机种子后,不使用加权策略对模型进行迭代数仅数百次的预训练,获取其损失项大致的数量级,再确定权重.流程框图如下所示.

本文第3 章中的算例均采用此算法确定损失函数权重值,确定的损失函数权重表可见附录B.

由于屈曲问题的模态,屈曲路径和屈曲载荷相对应,因此必须使用弧长法等迭代方法额外获得每一步的增量.具体可将当前神经网络求出的当前载荷的收敛位移Wepoch作为下一步的屈曲几何缺陷W∗代入屈曲控制方程求解屈曲附加挠度,这样在流程中,PINN 作为偏微分方程求解器使用,而外层使用弧长法进行控制,其迭代求解偏微分控制方程算法流程框图如图2 所示.

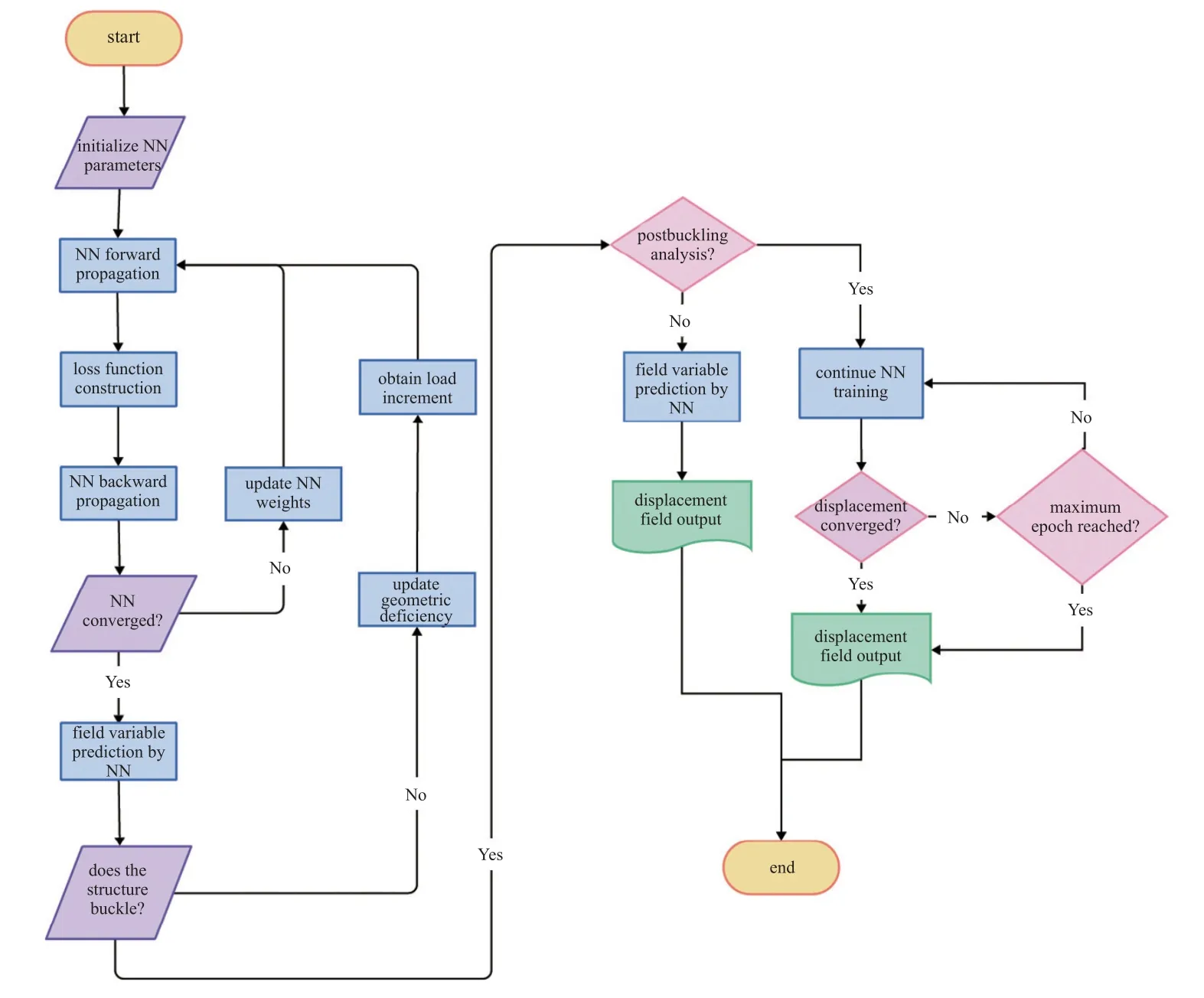
图2 以弧长法为外层控制的物理信息神经网络屈曲/后屈曲求解框图Fig.2 The framework of PINN as PDE sovler towards buckling/postbuckling problems governed by arcs method

弧长法在本文中作为PINN 的外层控制算法,当神经网络模型在拟合时达到了一定收敛度,便使用弧长法结束当前的神经网络迭代并计算下一步载荷增量,再将这一步的位移作为新的缺陷项替换神经网络中的缺陷项,最后利用神经网络进行下一步的学习.

使用弧长法求解PINN 得出的微分方程拟合解的增量并进行下一步求解的方法如算法2 所示.

在本文的流程中,预训练和正式训练时,默认求解域内部训练样本点NP=200,边界点NB=100.预训练时的训练次数iterpre取500 次,正式训练的最大训练次数itermax取40000 次.LPF误差容限 ε=0.01.对于测试集,另取样本点NT=100,两种样本点均采用拉丁超采样(LHS)方法生成.模型学习率初始为lr0=0.0001,设置学习率衰减为逆时衰减策略,即

衰减策略为每T=1000 轮衰减β=0.2.对于网络模型的初始化,采用Glorot 正态分布初始化器对参数进行初始化.

3 数值算例

3.1 受面内载荷的缺陷方板的屈曲和后屈曲

首先,对于一均质薄板的线性与非线性屈曲进行研究以验证PINN 的有效性.所研究的各向同性矩形板长宽尺寸均为a=1 m,厚度h=2 mm.材质为6 系铝合金,主要的力学性能为:弹性模量E=70 GPa,泊松比 ν=0.3,屈服应力280 MPa.设立3 种边界条件.分别为:①四边简支(SSSS);②对边简支对边固支(SCSC);③一对对边简支,另一对边一边固支一边自由(SCSF).其受载荷形式为在x=0,x=a两条简支对边上受边载荷Px.

先考虑其不带缺陷时,在不同的边界条件下所得到的屈曲模态和屈曲载荷,对于屈曲模态,由于其是满足方程边界条件的非平凡解,因此可以直接使用以载荷比例因子(LPF)为控制的迭代过程.由于PINN 本身的使泛化误差最小化的特质,如果其在迭代过程中不手动使载荷增加,而是直接对其设定估计的屈曲载荷值并让神经网络自身逼近,往往会得到平凡解和根据网络自身第一次迭代后的非0 载荷.

由PINN 方法计算的第一阶临界载荷和有限元结果的对比如表1 所示.

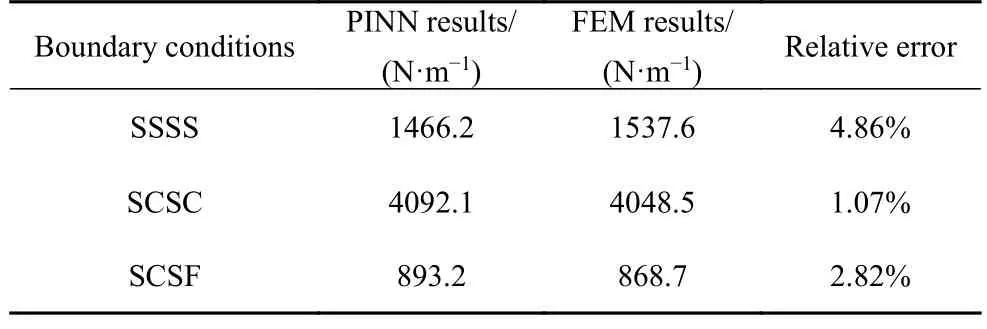
表1 第一阶屈曲模态对应的外载对比Table 1 The buckling load of the first buckling mode

可以看出,PINN 对于临界屈曲载荷能进行较好的预测,其和有限元相比,相对误差可以控制在5%以内.

对于薄板屈曲问题,由于其屈曲挠度分布极其容易受到初缺陷的影响,故将缺陷使用双三角级数表示,即

并采用高斯随机策略以模拟工程中具有初缺陷的薄板,其三角级数系数满足相互独立的正态分布

将式(18)作为缺陷代入控制方程,在接下来的算例中,取m=n=4 生成缺陷,并固定随机种子使得到的初缺陷表达式能够输入有限元软件内进行复现,最终得到的结果和有限元结果的对比如图3 所示.

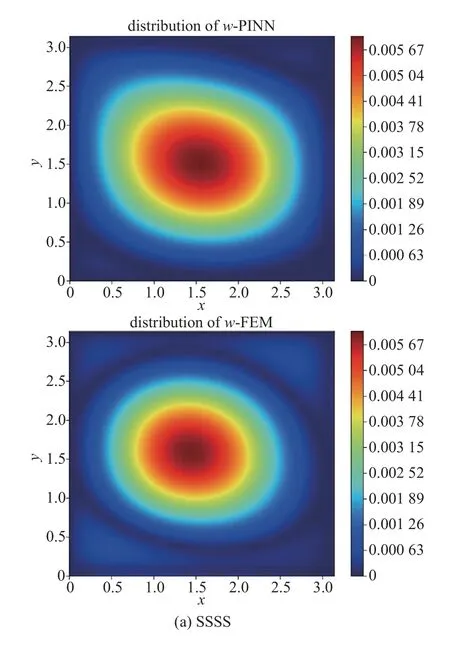
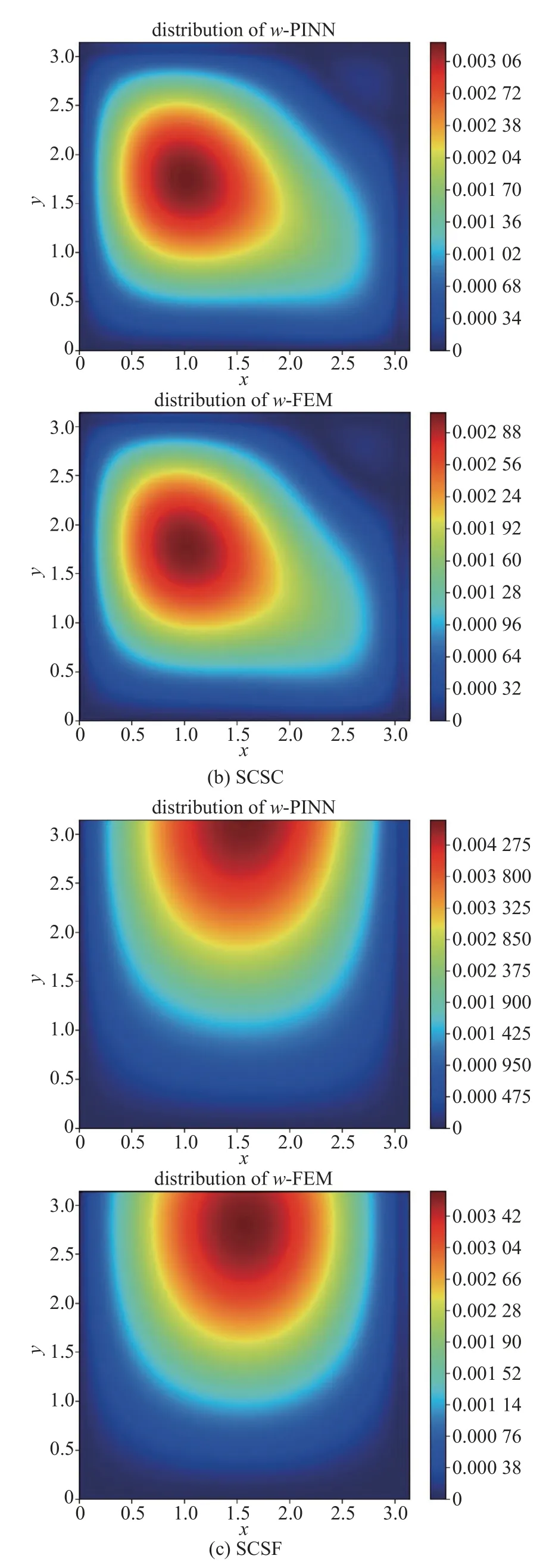
图3 带有缺陷的均质薄板的非线性屈曲位移云图对比 (上:PINN 结果,下:FEM 结果)Fig.3 The comparison of nonlinear buckling with deficiency (up:PINN results,down:FEM results)

综上结果可以看出,PINN 能够对完整薄板的线性屈曲的模态,第一阶屈曲载荷和缺陷薄板非线性屈曲的后屈曲做出很好的预测.这证明采用弧长法进行屈曲控制并通过PINN 求解器计算屈曲问题是可行的.

3.2 受轴压的缺陷薄壁圆筒壳

在本节中,使用PINN 方法针对一圆筒壳开展非线性后屈曲分析,图4 所示的圆筒壳半径R=1125 mm,高L=600 mm,厚度h=2 mm,材质与上节的薄板相同.边界条件为上下两圆周不可滑动简支,其他区域不做约束.

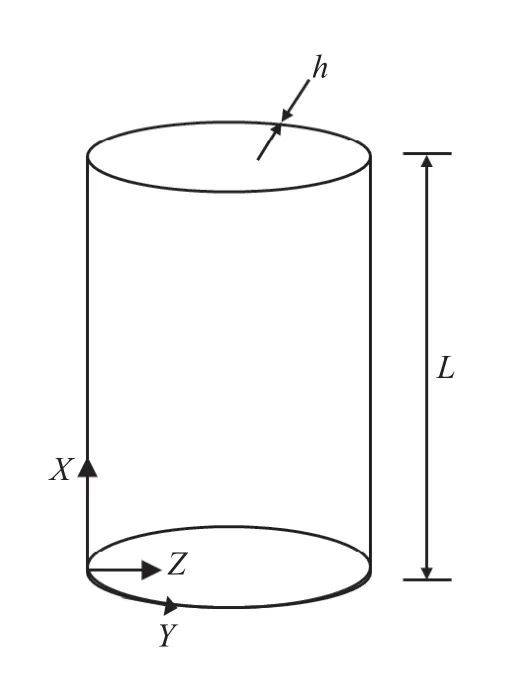
图4 薄壁圆筒壳及坐标系Fig.4 Thin-walled shell and its coordinate system

对于此算例,圆柱壳还特别地有周期性条件

对于此算例,考虑由初缺陷带来的几何非线性,使用3.1 中的初缺陷生成办法生成波形几何缺陷,进行非线性屈曲的研究.加载方式采用弧长法进行迭代,将无缺陷的圆筒壳的临界屈曲载荷作为基准,使用比例载荷因子进行加载控制.此外,为了规避数值计算中不同量级数据的舍入误差,对于此方程,引入无量纲化参数

式中,W与W∗分别是在屈曲作用下的挠度和因圆筒壳初始缺陷带来的几何初挠度,F为Airy 应力函数.将上述变换代入方程(6)中,得到对于薄壁圆筒壳的全局屈曲控制方程为

其中非线性项为

工程上通常关心前屈曲阶段的最大载荷因子,而后屈曲阶段的研究则主要以端部的最大缩短距离的变化趋势为主.

使用算法2,将迭代跳出判断条件改为

并将误差容限 ε 设置为足够小的正数,即可捕捉到屈曲载荷达到下降段前的最大比例载荷因子.对于后屈曲路径中最大缩短距离,取作为迭代终止条件,其表达式可用挠度表达为

两种方法生成的位移云图对比和不同网络参数得到的最大比例载荷因子见图5 和表2.

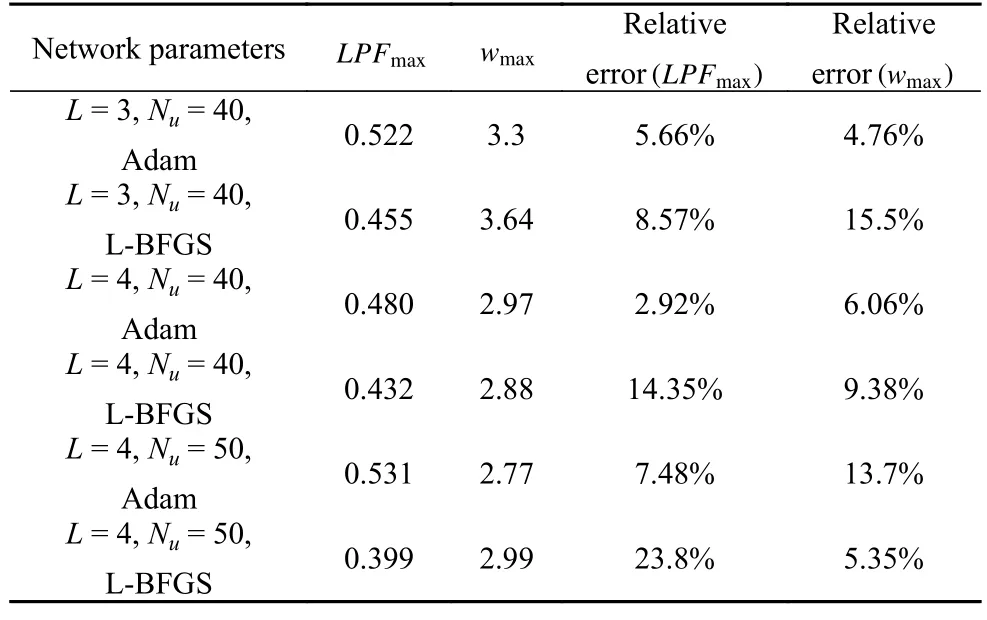
表2 带缺陷的圆筒壳屈曲行为最大比例载荷因子(LPFmax)与无量纲挠度 (wmax) 误差对比Table 2 The L PFmax and wmax of shell buckling with initial deficiency and their relative error

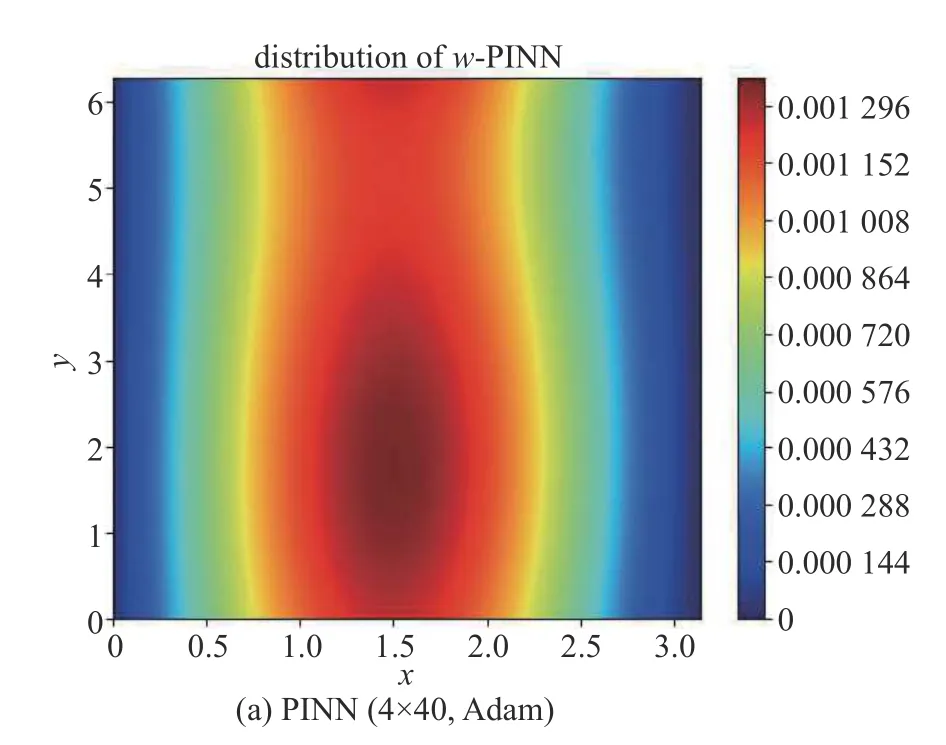
图5 带有缺陷的均质圆筒壳在最大 L PFmax 处非线性屈曲位移云图对比Fig.5 The comparison of nonlinear buckling displacement atLPFmax

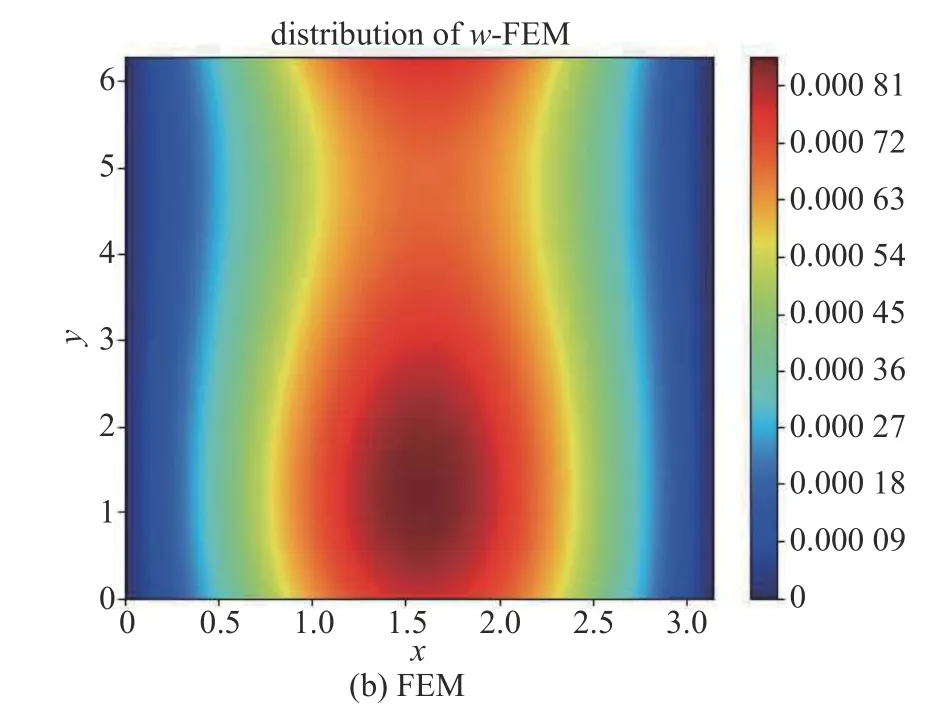
图5 带有缺陷的均质圆筒壳在最大 L PFmax 处非线性屈曲位移云图对比 (续)Fig.5 The comparison of nonlinear buckling displacement atLPFmax(continued)

从结果可以看出,神经网络方法,尤其是采用基于一阶导数优化的Adam 优化器进行神经网络的训练时,对最大承载时的位移模式求解较好,其位移分布和最大位移大小均和有限元结果接近.由PINN方法求出的轴压作用下后屈曲载荷-端部缩短曲线如图6 所示.

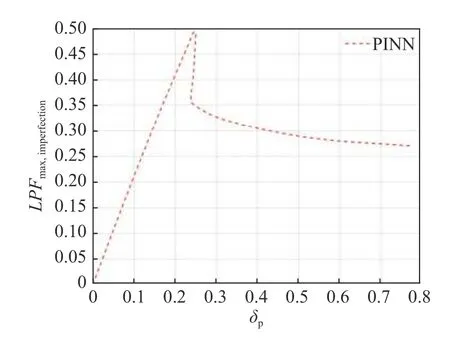
图6 后屈曲载荷-端部缩短曲线Fig.6 The end shrinkage plot of the cylindrical shell against LPF

3.3 圆柱筒壳的缺陷敏感度

以上两节的研究表明,初始几何缺陷的存在会对结构在屈曲过程中能达到的最大屈曲因子产生较大的影响,且根据文献[28],初始几何缺陷对屈曲载荷的影响对后屈曲最小载荷的影响更大.

图7 给出了在PINN 算法:有限元算法和Koiter理论解中对于此参数的圆筒壳缺陷敏感度的影响曲线.图中y轴为缺陷圆筒壳最大比例因子相对完整圆筒壳最大比例因子的比值,x轴为缺陷大小相对于筒壳厚度的比值.为了和已有结论做对比,调整厚度使半径与厚度比R/h=200.可以看出,PINN 计算出的缺陷敏感度要大于有限元的缺陷敏感度.值得注意的是,Koiter 理论由于使用同一个缺陷敏感度来描述缺陷敏感度,而没有考虑到筒壳本身的参数,对于此算例,其在经典圆筒壳理论中的Batdorf 壳体参数

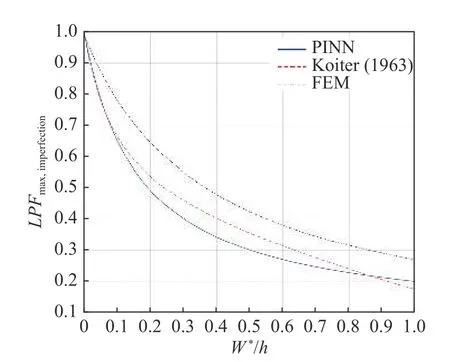
图7 圆筒壳的缺陷敏感度影响曲线Fig.7 Comparison of deficiency sensitivity of cylindrical shells

约为60,属中长壳范畴,结构后屈曲对缺陷敏感,PINN 和有限元算法都能较好地体现这一性质.

4 神经网络参数对收敛性影响

4.1 损失函数权重

在PINN 的训练过程中,损失权重的选取会极大地影响到神经网络的训练成功与否.对于构成复杂、组成部分数量级相差较大的损失函数,若不对其进行基于某种策略的平衡,势必会造成神经网络更偏重某一项损失函数的学习,而忽视了其他损失函数项.此处采用算例1 中带有缺陷的四边简支薄板来分析网络参数的变化对计算过程中误差函数的影响.图8 展示了未使用基于第2 章的权重调整策略(即权重分量默认为1)和使用了基于预训练权重调整策略对四边简支薄板损失函数的训练影响.其中横轴为训练周期数,纵轴为当前训练周期(epoch)的损失函数Lossepoch与第0 次(未训练)损失函数值Loss0比值的对数.

可以看出,更改权重对于此问题影响非常关键,采用了权重调整策略的PINN 模型对于损失函数的优化更好.同时为了排除PINN 撒点策略对结果产生的随机性影响,本章的算例均采用随机种子进行了多次实验.本章中曲线图由其平均值绘制,方差表可见附录C.

4.2 隐藏层层数 La 与神经元数目Nu

在实际求解过程中,隐藏层层数和每层的神经元个数选取会极大地影响到神经网络的训练效率和收敛性.在神经元总数过小或过大时,神经网络训练过程中会产生欠拟合和过拟合现象[31].而隐藏层层数在增加到一定程度时,神经网络损失函数随着训练次数的增加震荡会加剧[32].隐藏层层数和神经元数目对模型训练的结果影响如图9 所示.

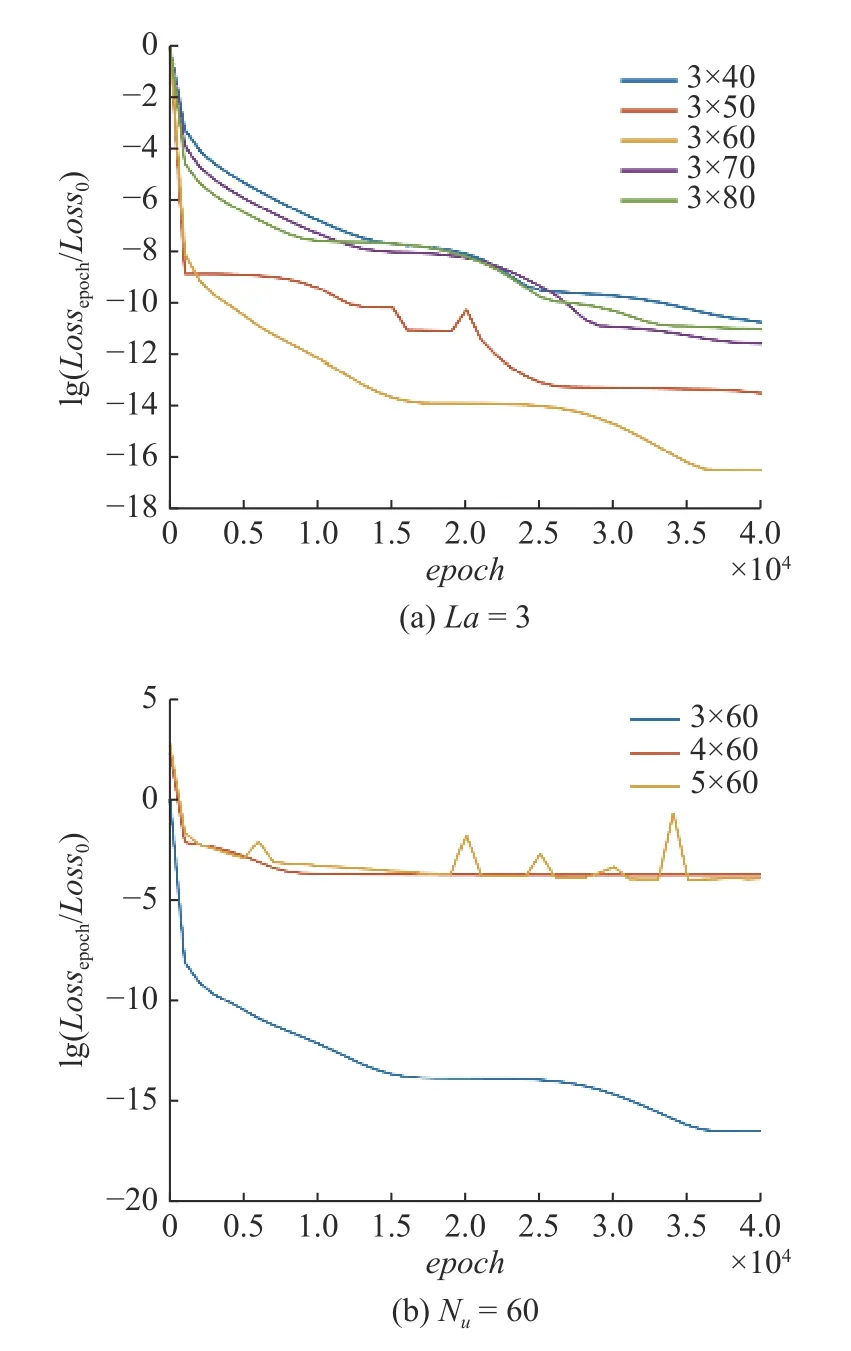
图9 不同网络参数对损失函数收敛特性的影响Fig.9 The influence of different network parameters to loss functions

从图9 中可以看出,对于算例1,隐藏层层数为3,每层神经元个数为60 左右可以达到最佳精度.相比之下,更多的隐藏层数目和神经元数目会加重计算硬件的负担,且不能保证更好的精度.总的来说,两者数量的选择仍然具有很强的经验性.另外,从图上可以看出,过大的隐藏层数目会加剧迭代过程中的震荡,而过多的每层神经元个数并没有对计算精度带来提升,更多神经网络参数对于计算精度的理论影响可参照文献[33-36].

4.3 求解器

本次实验所使用的深度学习平台为Tensorflow,Tensorflow 中自带了Adadelta,AdaGrad,Adam 和L-BFGS 等多种求解器,其基于的数学原理各不相同.以Adam 为基准,各优化器在其他神经网络参数相同的情况下对神经网络结果的影响如图10 和图11所示.

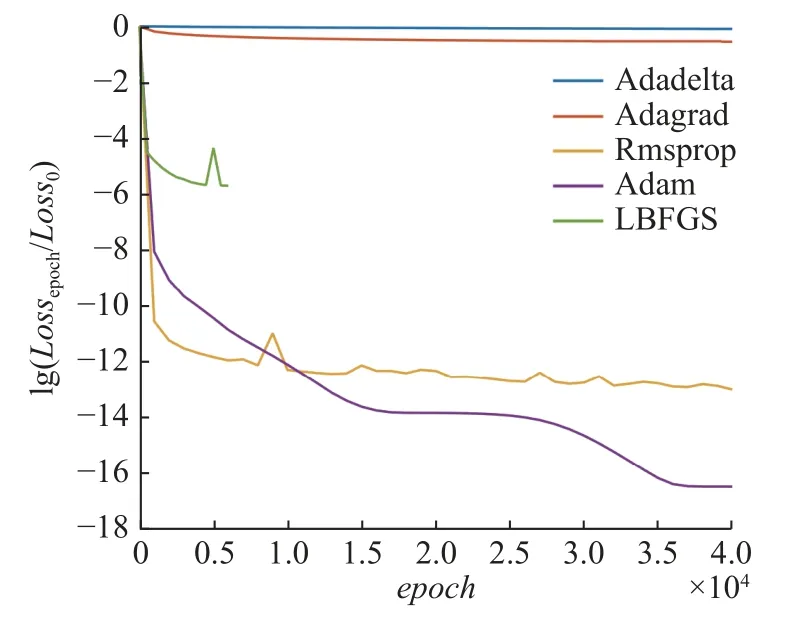
图11 使用各优化器时对损失函数的影响Fig.11 The influence of optimizers to loss functions

从图10 和图11 可以看出,L-BFGS 优化器由于是基于二阶梯度的方法,在所有优化器中有着最高的效率.在实际求解中,L-BFGS 优化器经常在达到最大训练次数之前就能使迭代步长小于误差容限ε从而停止继续训练.但根据重复实验的结果,L-BFGS 求解器更容易陷入局部最优解,从而不能得到真实的结果.一次典型的L-BFGS 陷入的局部最优解如图12 所示,可见其最大挠度过小.

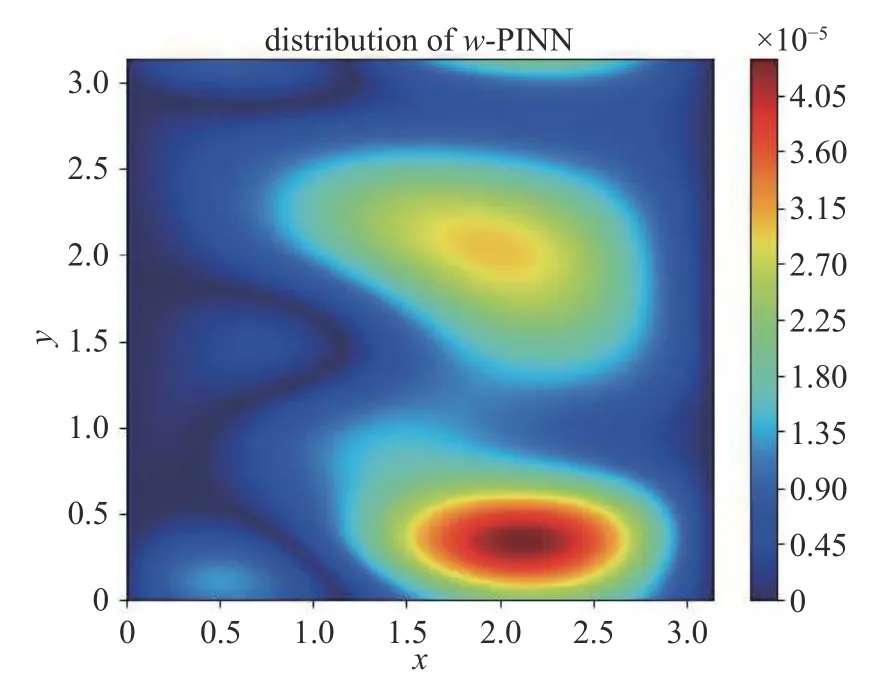
图12 L-BFGS 陷入的局部最优解Fig.12 The local optimum result that L-BFGS stuck with

4.4 激活函数

在神经网络的训练过程中,隐藏层的自适应非线性激活函数 σi可以基于多种基础的非线性函数进行构建.激活函数赋予神经网络的非线性性质能够让神经网络拟合各种非线性函数,常用的用于构建自适应激活函数的非线性函数有线性整流函数(relu),逻辑函数(sigmoid)和双曲正切函数(tanh)3 种,它们对均质薄板(SCSF)算例的影响如图13所示.其余两种函数的表现上,对于此学习率,双曲正切函数的收敛速度更好,但精度不如逻辑函数.值得注意的是,自适应relu 函数虽然取得了最小的损失函数数值,但在实验中作者观察到,由于其在x=0附近较为严重的导数不连续性,在算例中容易造成神经元死亡现象,因此不能正确地计算控制方程的损失函数项.在损失函数的变化曲线上,神经元死亡表现为在整个过程中曲线震荡较其他激活函数的曲线严重.一次典型的由于relu 函数特性导致其神经网络求出不符合物理规律的解的示意图如图14所示.

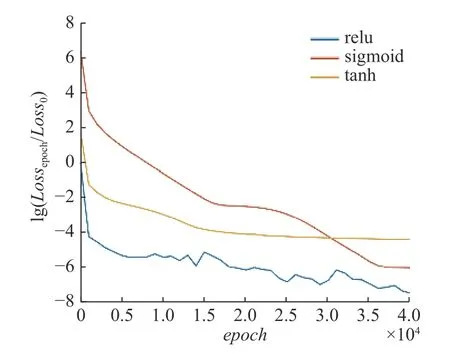
图13 均质薄板算例中不同激活函数对损失函数的影响Fig.13 The influence of the activation function on the loss function

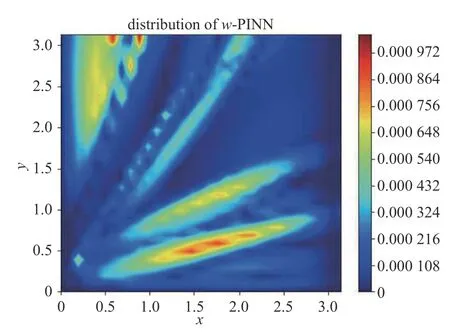
图14 relu 激活函数导致的求出不符合物理规律的解Fig.14 A result obtained by relu activation function that does not meet the governing equation

4.5 额外标签数据对第一阶屈曲载荷的影响

对于完整的板壳,由于其受到的壳边载荷在达到其第一阶屈曲载荷之前,其屈曲方程总是有平凡解,而非平凡解的变形模式必须在载荷大于临界载荷时才能出现.据此,可以将利用Rayleigh-Ritz 等能量方法假设出的变形形式作为标签数据输入到网络里.假设3 种薄板算例的第一阶屈曲模态分别为

系数A理论上在无缺陷板上可以取任意小的值,考虑到数值计算的特性,这里取A=0.1h,根据文献[29]中的图表,此时对应的屈曲载荷大约为线性屈曲理论的 101%∼105% 左右,本文取103% 作为对照值.将上述表达式在求解域上以均匀布点法选取40 个点,其标签记为 (xT,yT),T∈[1,40],获取的位移数据记为WT(xT,yT),并将这些位移数据作为位移得到标签数据输入到神经网络.这样PINN 就能额外在这些点上建立损失函数,其损失函数项为

之后进行物理信息神经网络训练,值得注意的是,由于已经提前让网络学习了屈曲的位移模式,网络可以直接求解控制方程而无需进行外层迭代.训练中可以发现,由于无需迭代和新增的标签数据损失函数,在拥有同样网络参数的物理信息神经网络下,拥有标签数据的神经网络训练较原有的神经网络收敛更快.但由于提前跳出,最终损失函数较迭代法更大,且相对误差更大.相应地,训练周期可减少到原有的一半左右.训练后的结果具体可见图15 与表3.

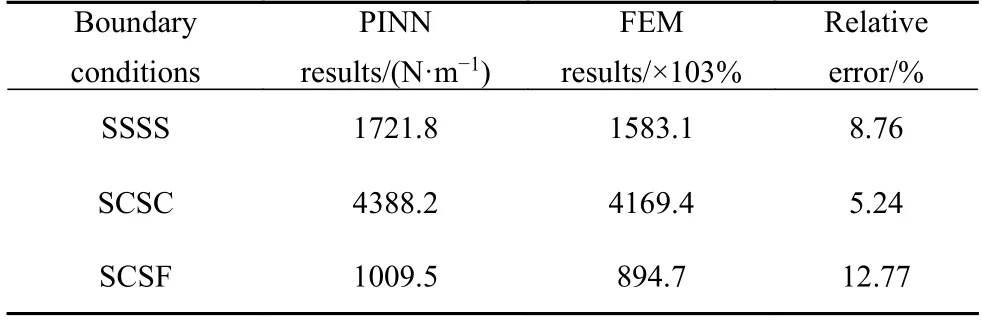
表3 拥有标签数据训练得到的第一阶屈曲载荷Table 3 The buckling load of the first buckling mode trained with labeled data

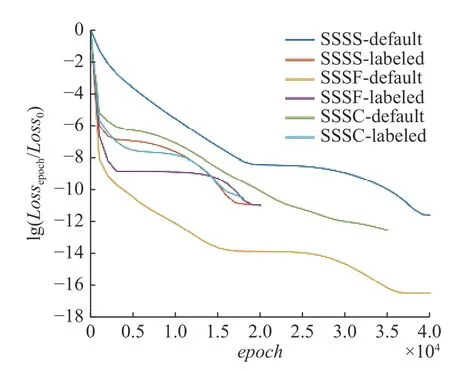
图15 标签数据对损失函数收敛特性的影响Fig.15 The influence of labeled data to loss functions

需要指出的是,在实际工程中,由于真实结构的边界条件十分复杂,要得到其屈曲模态几乎是不可能的.因此在工程中,要获得这样的标签数据难度较大,对于看重整个过程的屈曲问题更是如此.不可否认的是,标签数据可以提升神经网络求解效率,减少所需的计算资源,因此从工程实际中获得部分既容易测量又可供神经网络学习的高质量标签数据将是作者今后工作的重点之一.

5 PINN 与有限元效率对比

在DEEPXDE 中,PINN 的求解需要经历3 个步骤,分别为建立微分方程及数据(build),编译损失函数(compile)和训练神经网络(train).本文部分算例求解时迭代所需的平均时间及时间的组成如图16所示.从图中可以看出,PINN 方法耗时最长的部分是训练神经网络部分,不论是迭代到误差容限以下结束训练,还是迭代至最大训练数,训练损失函数部分通常需要占据神经网络训练总时长的80%～90%左右,并且由于非线性屈曲问题的迭代特性,使得时间复杂度进一步提升.

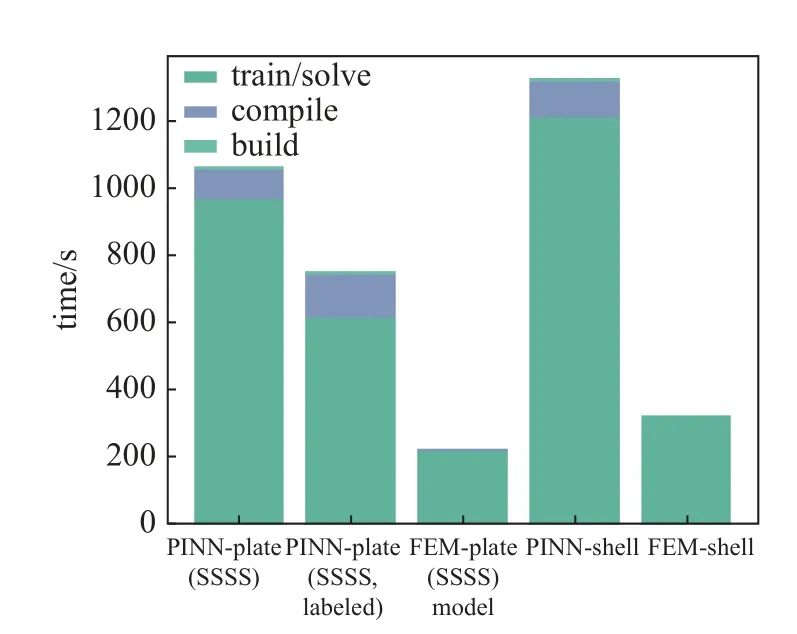
图16 本文算例所需时间及其组成Fig.16 The computation time of the numerical examples and its composition

本文的有限元结果由商业有限元软件Abaqus 2021 得到,其中线性屈曲载荷由求解器“Linear perturbation,Buckle”求得,而非线性屈曲模态和最大载荷因子则由求解器“Static,Riks”求得.从图16 可以看出PINN 方法相对成熟度高的商业有限元软件计算效率偏低,其原因主要有以下几点:(1) PINN 求解的是强形式的控制方程,其损失函数虽然能够表征物理规律,但对应的优化问题有可能高度非凸,总体需要的计算量大.(2) 商业有限元软件具有成熟高效的求解流程,在每一步的计算效率较高.(3) PINN在求解时需要更多的单轮迭代步骤.即使有了额外的数据标签,其求解效率也仅有部分提高.有限元软件是直接求解弱形式的物理方程,单轮迭代一次仅需要求解一次方程.因此计算效率更高.

6 结论与展望

本文基于深度学习技术、屈曲控制方程的强形式求解与迭代法建立了一种求解薄壁板壳结构屈曲问题的神经网络方法.通过两种典型结构的算例,可以得出以下几个结论.

(1) 本方法的结果与有限元结果的误差大多时候能控制在10%以内,且在数据驱动方面不需要额外的挠度和力学量数据,这一特性展现了此方法在工程中的实用性和合理性.

(2) 本方法的结果是对强形式偏微分控制方程进行求解的结果,因此数值解具备相对于控制方程的连续性,满足物理定律,这一点有别于一般数值驱动神经网络所带来的结果,但由于屈曲问题的数据集收集较为困难,本文未能将PINN 结果和一般数据驱动的神经网络结果作对比.

(3) 由于屈曲临界载荷和物理信息神经网络本身都需要进行迭代,因此本文方法在计算部分的时间复杂度上劣于传统的有限元方法,但其不需要网格前处理的特性有望减少解决复杂问题时的整体工作量.

根据目前所得出的结论,进一步工作可以从以下几个方面展开.

(1) 本文所建立的神经网络模型采用了硬边界约束(hard constraint),其本质是构造满足边界条件的试函数并在输入层进行变换使神经网络的拟合解能够满足边界条件,这一部分仍然具有较强的经验性,有待实现自动化,有兴趣的读者可参考文献[36].

(2) 由4.5 节可见,标签数据对增加PINN 训练效率、减少计算资源使用有着较为显著的作用,但本文算例中给出的标签数据可以较为简单地获取,而实际工程中则不然.因此,如何从工程实际结构中获得容易测量又可作为额外标签的物理量提供给PINN 学习将会是PINN 算法在实际工程运用中一个十分有前景的问题.

(3) 本文所建立的神经网络模型仍然是建立在人为经验的基础上,因此具有较大的优化空间,其中一个可改进的方面是优化隐藏层的布置,例如卷积层等其他神经函数隐藏层用于神经网络学习屈曲模式.此有望用于在复杂结构的屈曲过程中判断屈曲模式,为实际工程优化问题提供进一步解决方案.

附录A:本文主要符号变量表