刘志娟 （江苏省如东县马塘镇邱陞中学）

当前初中生主要通过做题提高解题能力，除了做题，学生其他方面的体验比较少。就做题而言，学生往往做的是答案唯一的题目。基于以上两点原因，要想进一步提高学生的解题能力就需要教师丰富学生的体验，同时还需要增加一些开放式题型。开放式题型往往因为设置的灵活性和思考的多维性更能促进学生思维的发展，也更能考查学生的解题能力。因此，教师要多设置开放式题型锻炼学生的解题能力。

一、设置问题不固定题目

对于数学学习来说，学生不仅要学会解决问题，还要学会发现问题。当前的数学教学大多时候是教师呈现问题，学生解决问题。在这样的教学模式下，学生发现问题的能力会减弱，不利于解题能力的提高。因此，在设置题目时，教师可以先设置一个情境，让学生根据情境自己设置不同的问题。

问题情境：如图1，学校统计学生早晨到校情况，从7：00开始校门口的学生人数y（单位：人）随时间x（单位：分）变化情况的图象是二次函数的一部分。

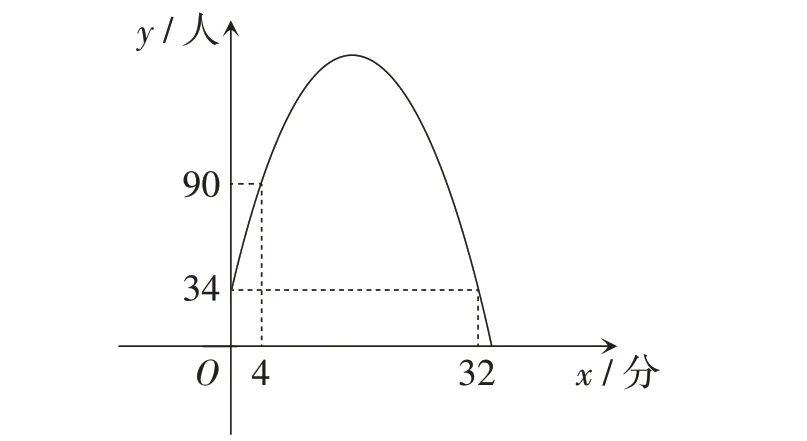
图1

教师先让学生对照函数图象和情境内容提出问题。学生首先想到的是求y与x之间的函数解析式。对此，先设y与x之间的函数解析式为y=ax2+bx+c，对照图象中给出的数据列出方程组，得解得所以教师鼓励学生继续提出问题，同时引导学生将题目的表述与图象结合起来。看到图象中变化的曲线，学生提出这样的问题：“从7：00 开始，学生在什么时间能全部进入学校？”提出问题之后，学生在合作中转化问题，发现问题的本质是求函数图象与x轴的交点。令y=0，即解得x1=-2（舍），x2=34。所以学生在7：34时全部进入校园。

从整个解题过程来看，学生要先提高读图能力，能将题干中的表述与所给图象对应起来。同时，学生还要提高借助图象发现问题的能力，主动建构学习。设置问题不固定的开放式题型，能使学生根据自己的认知情况和学习能力提出与自己数学学习水平相当的问题。教师从学生的提问中可以发现他们的思维特点，进而进行针对性引导，促进学生解题能力的提高。学生自己提问，不仅增强了他们学习的主动性，还增强了解题的趣味性，使他们更愿意参与其中。

二、设置结论不固定题目

教师可以设置一些结论不固定的题目，以增加学生探究的机会。所谓结论不固定，就是教师只呈现题目的条件，进而让学生依据条件推理出可能存在的结论。结论不固定题目可以给予学生更多思考的空间，也能提高他们的解题能力。教师要引导学生不仅要从条件出发，推断出可能出现的结论，还要从结论出发进行逆向论证，以验证条件是否充分利用。

题目1如图2，将平行四边形ABCD沿一条直线折叠，使点A与点C重合，点D落在点G处，折痕为EF，你能发现哪些结论？

图2

学生先直观感知题目，接着拿出一张纸剪成平行四边形，进而标出对应的字母，再按照题目要求折叠。在折叠的过程中，他们相继发现∠A=∠BCD，∠A=∠ECG， ∠ECB=∠FCG。观察的过程其实就是学生解题的过程，观察能力是重要的解题能力。观察得出结论后，便开始证明。学生先由四边形ABCD是平行四边形得到∠A=∠BCD。再根据折叠的性质得到∠A=∠ECG，最后由∠BCD-∠ECF=∠ECG- ∠ECF，得∠ECB=∠FCG。教师追问：“是否有新的发现？”学生在折叠的过程中除了发现相等的角，还发现了一些相等的边，由此他们猜想能不能找到全等三角形。基于发现的相等的角和相等的边，学生发现△EBC≌△FGC，接着开始证明。学生由四边形ABCD是平行四边形，得∠D=∠B，AD=BC。再由折叠的性质，得∠G=∠D，CG=AD，所以∠B=∠G，BC=CG。因为∠ECB=∠FCG，所以△EBC≌△FGC()ASA。学生对照题目给出的条件，在操作、观察中运用平行四边形的性质、折叠的性质、全等三角形的判定等知识，完成了对结论的猜测与证明，提高了自己的解题能力。

三、设置解法不固定题目

开放式题型能激发学生的思维火花，让学生更多地关注解题过程，而不再是一味地强调解题结果。解法不固定也是开放式题型的一种，即学生可以采用多样的方式解决问题。教师可以鼓励学生从不同的维度思考问题，拓宽解题思路的同时提高解题能力。

题目2如图3，直线y=kx+ 8 与抛物线相交于两点。

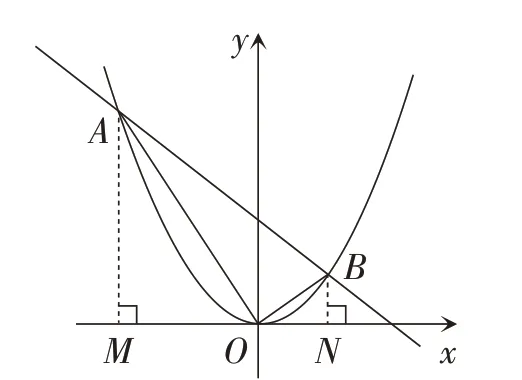
图3

求证：（1）点(y1，y2)在反比例函数的图象上；

（2）x1OB+y2OA=0。

对于第（1）小题，学生根据题意得出x2-8kx-64=0，进而得出x1x2= -64。因为所以可见点(y1，y2)在反比例函数的图象上。对于第（2）小题，学生先想到了运用勾股定理直接表示OA，OB的长。由题意，知再由第（1）小题的结论得进而推出又因为x1＜0，y2＞0，所以-x1OB=y2OA，即x1OB+y2OA=0。完成证明后，学生想能不能将要证明的式子变形，写成比的形式，再根据OA，OB为线段，将x1，y2与线段长度联系起来。于是，学生过点A分别作AM⊥Ox，BN⊥Ox，垂足分别为点M，N。同样地，利用第（1）小题的结论，由-x1x2=y1y2=64 得出OM·ON=AM·BN，即又因为∠AMO=∠ONB=90°，所以△AMO∽△ONB，进而推断出即OM·OB=BN·OA。将这个等式化简，得-x1OB=y2OA，即x1OB+y2OA=0。当完成第二种解法后，学生在想：有没有第三种解法呢？他们运用解析式法，结合第（1）小题，由得出OA⊥OB，从而得到进而也得出从而得出最后的结果x1OB+y2OA=0。因此，教师要鼓励学生多想一想有没有更多的解法，要尽可能地创设解法多样的题目，激活学生的思维，提高解题能力。

综上所述，开放式题型能给学生提供更多思考的空间。教师可以依据学生的实际情况创设一些开放式题型，扩大学生思考的范围和思维的深度，促使学生养成深度思考的习惯，进而提高解题能力。