Yun‐Shan Wei| Jin‐Fan Wang | Jia‐Xuan Wang | Qing‐Yuan Xu| Jaime Lloret

1School of Electronics and Communication Engineering, Guangzhou University,Guangzhou,China

2School of Electronic and Information,Guangdong Polytechnic Normal University,Guangzhou,China

3Universitat Politècnica de València, Valencia, Spain

Abstract For linear time varying (LTV) multiple input multiple output (MIMO) systems with vector relative degree, an open-closed-loop iterative learning control (ILC) strategy is developed in this article, where the time interval of operation is iteration dependent.To compensate the missing tracking signal caused by iteration dependent interval, the feedback control is introduced in ILC design.As the tracking signal of many continuous iterations is lost in a certain interval, the feedback control part can employ the tracking signal of current iteration for compensation.Under the assumption that the initial state vibrates around the desired initial state uniformly in mathematical expectation sense,the expectation of ILC tracking error can converge to zero as the number of iteration tends to infinity.Under the circumstance that the initial state varies around the desired initial state with a bound, as the number of iteration tends to infinity, the expectation of ILC tracking error can be driven to a bounded range, whose upper bound is proportional to the fluctuation.It is revealed that the convergence condition is dependent on the feedforward control gains, while the feedback control can accelerate convergence speed by selecting appropriate feedback control gains.As a special case,the controlled system with integrated high relative degree is also addressed by proposing a simplified iteration dependent interval based open-closed-loop ILC method.Finally,the effectiveness of the developed iteration dependent interval based open-closed-loop ILC is illustrated by a simulation example with two cases on initial state.

K E Y W O R D S intelligent control, iterative methods

1 | INTRODUCTION

Different from the model based control techniques[1–6],as an intelligent control scheme, iterative learning control (ILC) is usually utilised to impel the output of repetitive system to track a reference trajectory gradually along the iteration direction[7–10].By employing the tracking information of preceding iterations, ILC adjusts the control input of subsequent iterations to make the tracking error reduce.One of the most conspicuous strengths of ILC is that less prior knowledge of the dynamical system is required in design process, which makes ILC popular in both theoretical and applicable fields with repetitive cases such as robot [11–13], high speed rack feeder [14], high speed train [15–17], pneumatic artificial muscle [18], and air conditioning system [19].

With the aim of achieving perfect tracking, most ILC methods require that the time interval at each iteration is fixed.However, in many actual circumstances, the controlled system may stop earlier or later due to external disturbances or system dynamics.This would lead to the time interval varies from iteration to iteration.Thus, some ILC designs for dynamical systems with iteration dependent interval have been investigated[14,20–38].And the authors in the work[39]have provided a review of the model and ILC method of the iteration dependent interval systems.In [20], a certain convergence is derived with the help of improved P-type ILC scheme for non-linear systems with iteration dependent interval initial state,and external disturbances.Other first order ILC schemes can be found in [21, 22], and [23].Due to the iteration dependent interval, the tracking signal of last cycle would be lost as the actual time interval is less than the desired one.In this case, the mentioned first order ILC schemes, which only utilise the tracking signal of last cycle to adjust current control input,cannot obtain useful information from last iteration.To deal with the iteration dependent time interval, for linear discrete time systems, the iteration average operator is introduced in [24], where all former tracking signals are collected and employed to compensate the missing information.In[25],an iteratively moving average operator is introduced in ILC design,which uses the tracking information of latest iterations to compensate the signal that was missing at last iteration.For non-linear systems with initial state shifts and iteration dependent interval, a higher order ILC scheme using the information in some recent iterations is proposed in[26].In[27],two ILC schemes are presented,which select valuable tracking information and filter out redundant information.Some other ILC schemes with the compensation mechanisms in iteration domain are presented for linear systems[28–30]and non-linear systems [31–37].Combining flexible adaptive methods and two-dimensional methods,some novel ILC schemes have been addressed for a class of iteration dependent interval repetitive systems [35–38].However, it is worth pointed out that these iteration based compensation methods [24–33] need to store lots of tracking information.As the time interval is shorter in many continuous iterations,the storage of ILC would be large,since the signal in many previous iterations are adopted in ILC law.Other compensation mechanisms should be considered for dynamical systems with iteration dependent interval.

On the other hand, most of the existing iteration dependent interval based ILC methods are developed for controlled systems with a relative degree of one [20–27, 30–33].For dynamical systems represented in time domain, the relative degree reflects that the control input affects the system output connected with system matrices [40–43].And for linear systems represented in frequency domain by a transfer functionU(s)/V(s), the relative degree is defined byG=degV-degU, where deg(⋅) denotes the order of polynomial with real coefficients.Nowadays, the ILC issue of dynamical systems with high relative degree(G>1)are studied[41–43].The vector relative degree of multiple input multiple output (MIMO) systems reveals the relationship from control input to single system output, which can give more detailed information between them.Fortunately, in recent years, the iteratively moving average operator based ILC scheme with robustness analysis is proposed for linear continuous time systems with vector relative degree under iteration dependent input trail lengths and random initial state shifts[28].For linear discrete time MIMO systems with vector relative degree and iteration dependent interval, an iteration average operator based PD-type ILC is presented,as well as P-type and D-type[29].The authors in the work[34]used the modified error and iteratively moving average operator to design two iteratively variable pass lengths based sampled data ILC algorithms for non-linear continuous time systems with vector relative degree.However,the systems considered in[28,29]are time invariant,and the missing information caused by iteration dependent interval is compensated by the signal of previous iterations[28,29, 34].More efforts should be made in iteration dependent interval based ILC scheme for time varying systems with vector relative degree.

In this paper, an iteration dependent interval based openclosed-loop ILC scheme including feedforward and feedback control structure is developed for linear time varying (LTV)MIMO systems with vector relative degree.As the tracking information of many continuous iterations is lost in a certain time interval, the signal of current iteration could be used for compensation with the help of feedback control item.Under the assumption that the initial state vibrates around the desired initial state uniformly in mathematical expectation sense, the expectation of ILC tracking error can converge to zero as the number of iteration tends to infinity.Under the circumstance that the initial state varies around the desired initial state with a bound, as the number of iteration tends to infinity, the expectation of ILC tracking error can be driven to a bounded range,whose upper bound is proportional to the fluctuation.It is demonstrated that the convergence condition is dependent on the feedforward gains only, while the appropriate feedback gains can improve the ILC convergence performance.As a special case,the controlled system with integrated high relative degree is also addressed by proposing a simplified iteration dependent interval based open-closed-loop ILC method.The major contributions of this paper are summarised as follows:(1) the existing iteration dependent interval based ILC studies for MIMO systems with vector relative degree requires that the system is time invariant[28,29].The LTV MIMO system with vector relative degree or integrated high relative degree is considered in this article.(2)In the ILC designs for dynamical MIMO systems with iteration dependent interval, the tracking information in previous iterations is adopted for compensation[28–37].An iteration dependent interval based open-closedloop ILC method containing feedforward and feedback control is proposed.With the help of feedback control, a compensation mechanism in time domain is presented, such that the missing tracking signal caused by iteration dependent interval can be compensated by the signal of current iteration.The proposed iteration dependent interval based open-closedloop ILC method can accelerate the convergence speed with the help of appropriate feedback control gains.(3) To analyse the convergence of the proposed iteration dependent interval based ILC schemes,theλ-norm is widely used[22,24,25,27,30–34].However, it is well known that theλ-norm might not be satisfactory measure of ILC tracking error [26, 29].By employing mathematical induction in convergence analysis,λnorm is avoided in this article.

The remaining sections of this article are organised as follows.In Section 2, the LTV MIMO system with vector degree and iteration dependent time interval is presented, as well as some preliminaries.Under the initial state vibrates around the desired initial state uniformly in mathematical expectation sense, the developed iteration dependent openclosed-loop ILC method and the convergence analysis are given in Section 3.When the initial state varies around the desired initial state with a bound, Section 4 provides the corresponding robustness analysis.Section 5 provides a simulation example to validate the effectiveness of the

2 | PROBLEM DESCRIPTION AND PRELIMINARIES

Consider the following LTV MIMO systems that operate repetitively,derived results.In the end, we conclude this article in Section 6.

whereGs>1.

Assume that there is a unique control inputud(z)∈Rrfor 0 ≤z≤Zd, such that

where(z)is the s-th component of yk(z)at k-th iteration.

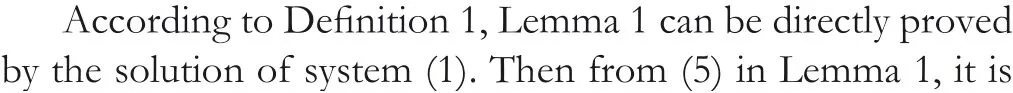
In order to investigate the iteration dependent interval based ILC method for LTV MIMO systems with vector relative degree, letE(η) be the mathematical expectation of the stochastic variableη.Then we give the following assumptions.

Remark1.In traditional ILC schemes,a common assumption is that the statexk(0) at each iteration is equal to the desired initial statexd(0) [25].Comparing with it, Assumption 1 is relaxed,which allowsxk(0)varying uniformly aroundxd(0)in mathematical expectation sense[24].Assumption 2 is a general case of Assumption 1.It is worth noted that the strict requirement of identical initial condition in traditional ILC studies is relaxed under both Assumptions 1 and 2.

Moreover, the iteration dependent interval issue is also considered in this paper.In other words, the actual terminal time stepZkis iterative varying and different from the desired oneZd.For that case, a Bernoulli stochastic variableλk(z)(0 ≤z≤Z) taking binary values 0 and one is introduced.On the one hand,λk(z)=1 occurring with probabilityq(z),(0 ≤q(z)≤1)indicates that the ILC process of system(1)can continue to the time pointzatk-th iteration.On the other hand,λk(z)=0 occurring with probability 1-q(z) indicates that the ILC process of system(1)cannot continue to the time pointzatk-th iteration.

which implies

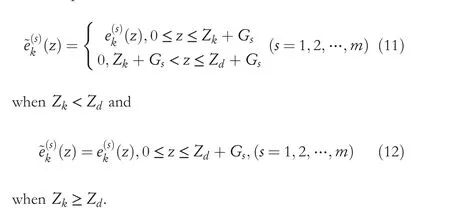
3 | ITERATION DEPENDENT INTERVAL BASED OPEN‐CLOSED‐LOOP ILC DESIGN AND CONVERGENCE ANALYSIS

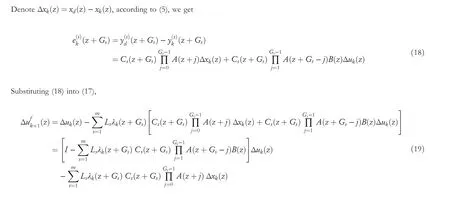
Subtracting both side of (13) withud(z), and considering (15) and (10), it yields

Substituting (20) into (19),

Applying norm ‖⋅‖ andE｛⋅｝ on both sides of (21), we have

According to the definition of Bernoulli stochastic variableλk(z), there are

and

On the other hand, from (23), (16) and (24), we can rewrite (22) as

According to (5) in Lemma 1 and (26), we have

In consequence, from (26) and (27), we can get

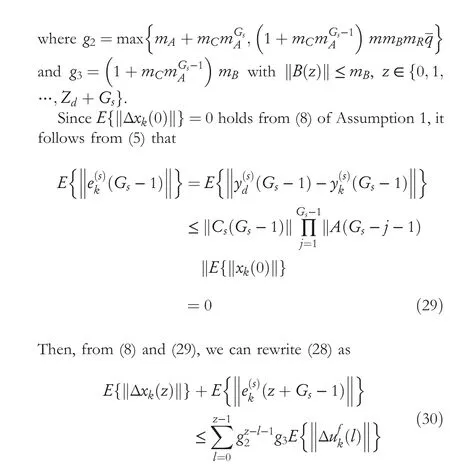
Consequently, substituting (30) into (25), it yields

Thus, based on the mathematical induction, we can conclude that

Similar to Lemma 1, we obtain the following relationship according to(42)and(1),

Therefore, the following Corollary 1 to Theorem 1 is derived.

Corollary 1.For system(1)with integrated high relative degree G>1,under Assumption 1,assume the desired output trajectory yd(z)is realized.Apply the following simplified iteration dependent interval based open-closed-loop ILC law for0 ≤z≤Zd,

4 | ITERATION DEPENDENT INTERVAL BASED OPEN‐CLOSED‐LOOP ILC DESIGN UNDER INITIAL STATE FLUCTUATION

In practice,the initial state in most ILC applications might not vibrate uniformly,which means that condition(8)of Assumption 1 does not satisfy.To address this case,a more relaxed initial condition should be considered.In this section,under the initial state fluctuation described in(9)of Assumption 2 rather than(8)of Assumption 1, the corresponding robustness analysis is provided.

Then, from (9) and (48), we can rewrite (28) as

Asz=v, from (50), we have

Applying Lemma 2 to(56)and considering(52),(55),and(16),we obtain

Thus, based on the mathematical induction, we can conclude that

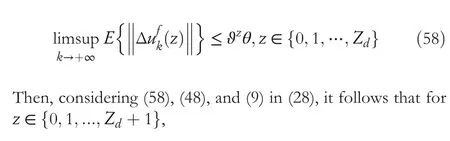
This completes the proof.

Remark2.Theorem 2 gives the robustness analysis of iteration dependent interval based open-closed-loop ILC scheme under initial state fluctuation.From the theoretical results, one can see that the asymptotic bound of ILC tracking error is dependent on the bound of initial state fluctuation.In practice,we can drive the tracking error into an acceptable range by precisely setting the initial position.

Similar to Corollary 1, the following Corollary 2 to Theorem two is acquired.

Remark3.In some ILC studies for linear MIMO system with integrated high relative degree, they require that the system is time invariant and operates in fixed time interval [42, 43].Corollaries 1 and 2 gives the simplified iteration dependent interval based open-closed-loop ILC law for LTV MIMO systems with integrated high relative degree, which in fact extends the ILC designs for MIMO system with integrated high relative degree to a wider range.

5 | SIMULATION EXAMPLE

Example 1.To illustrate the effectiveness of the developed iteration dependent interval based open-closed-loop ILC method, consider the LTV MIMO system with vector relative degreeG=(1,2) denoted as

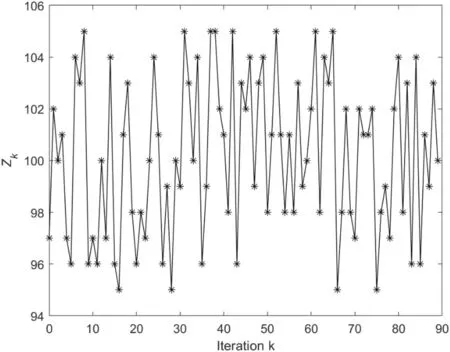
whereZd=100.The iteration dependent terminal time stepZk∈｛95,96,…,105｝ is displayed in Figure 1.Afterwards,system (61) with ILC law (13)–(15) is simulated.The performance of ILC is evaluated by the following error index on the sum of absolute errors,control item involved with ILC design can use the tracking error information of current iteration to compensate the missing signal due to the presence of iteration dependent time interval.Even if the open-closed-loop ILC law is a little more complicated than the traditional P-type ILC law for discrete time system, it can achieve a better transient response and convergence speed because there are more control gains to adjust.

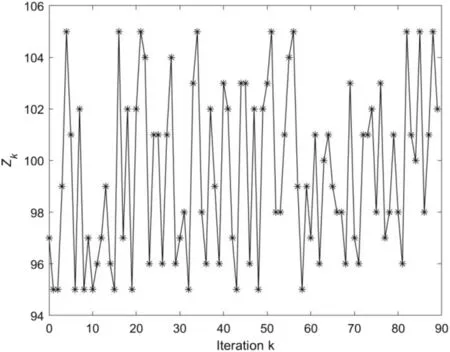
F I G U R E 1 The variation of iteration dependent terminal time step Zk versus iteration k.

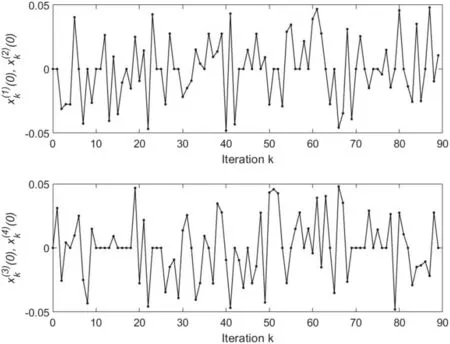
F I G U R E 2 (case 1 of Example 1):The profiles of initial states (0),(i=1,2) (above) and (0), (i=3,4) versus iteration k as the values of initial state satisfy E｛‖xd(0)-xk(0)‖｝=0 with xd(0)= [0 0 0 0]T.

F I G U R E 4 (case 1 of Example 1): The resulting output trajectories(z)to the desired output trajectory(z)(above)and z)to the(z)(below) at iterations k=3 and k=5.

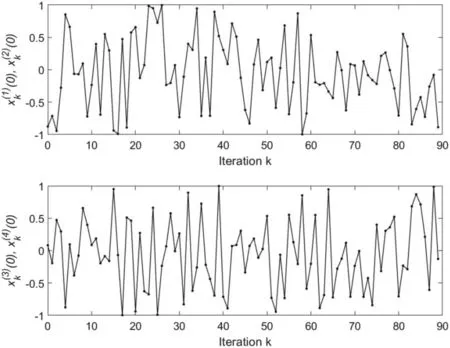
F I G U R E 5 (case 2 of Example 1):The profiles of initial states (0),(i=1,2) (above) and (0), (i=3,4) versus iteration k as the values of initial state satisfies E｛‖xd(0)-xk(0)‖｝≤δ with xd(0)= [0 0 0 0]T and δ=1.

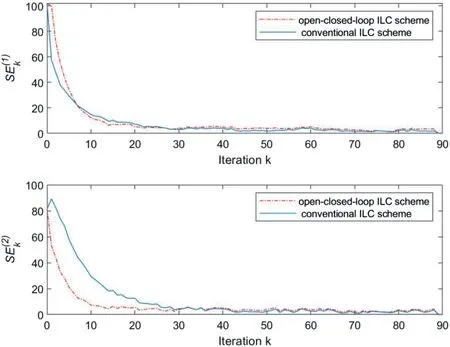
F I G U R E 6 (case 2 of Example 1): The profiles of the error indexes S(above) and S(below) versus iteration k.

Example 2.To illustrate the effectiveness of the simplified open-closed-loop ILC law (44)–(46), consider the following linear piezoelectric motor system with relative degreeG=2 under iteration dependent interval, which is described as follows [44]wherez∈｛0,1,...,100｝ withZd=100.The initial control inputu0(z)=0 forz∈｛0,1,...,100｝.In order to measure the ILC performance, the tracking error index is defined as

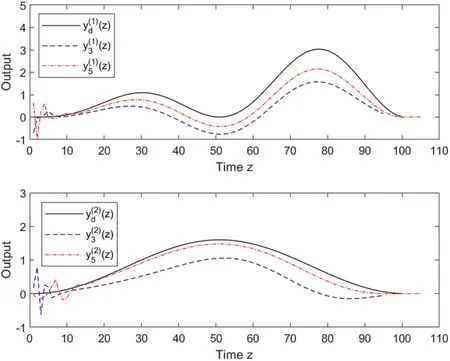
F I G U R E 7 (case 2 of Example 1): The resulting output trajectories(z)to the desired output trajectory (z)(above)and (z)to the(z)(below) at iterations k=3 and k=5.

Apply the developed ILC law (13)–(15) withG=2,L=14.5, andR=11 to system (65).In the simulation, two cases on initial state are provided under Assumption 1 and 2,respectively.

Case1.The values of the iterative initial state are set asxk(0)=xd(0)= [0 0]T, which satisfy Assumption 1.The corresponding tracking error indexSEkalong the iteration direction is depicted in Figure 9.Figure 10 provides the responding output trajectoryyk(z) to the desired output trajectoryyd(z) at iterationsk=3 andk=5 by adopting the simplified open-closed-loop ILC law (44)–(46).

F I G U R E 8 (Example 2):The variation of iteration dependent terminal time step Zk versus iteration k.

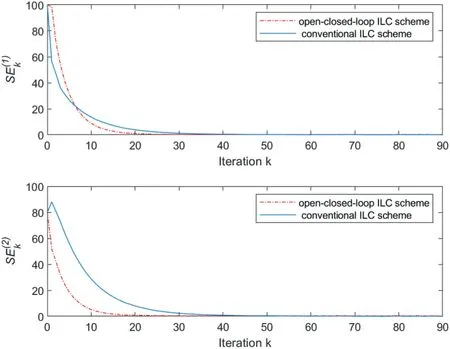
For system (65) with relative degreeG=2, as the iterative initial statexk(0)=xd(0)= [0 0]Tsatisfying Assumption 1,it is illustrated from Figure 9 that the tracking error indexSEkcan be controlled to zero.From Figure 10,it can be seen that aprogressively improved tracking performance of system outputyk(z)to desired output trajectoryyd(z)has been accomplished forz∈｛0,1,...,100｝.Corollary one is verified.For system(65) with relative degreeG=2, as the iterative initial state varies around the desired initial state with a bound that is,E｛‖xd(0)-xk(0)‖｝≤δas shown in Figure 11 satisfying Assumption 2,Figure 12 illustrates that the control error indexSEkcan be driven to a bounded range.From Figure 13, it is shown that the corresponding output trajectory can track the desired output trajectory progressively along the iteration direction.Corollary two is verified.In addition,Figures 9 and 12 demonstrate that the proposed simplified iteration dependent based open-closed-loop ILC law (44)–(46) has a faster speed than the conventional P-type ILC without feedback control part shown as (44) and (45).

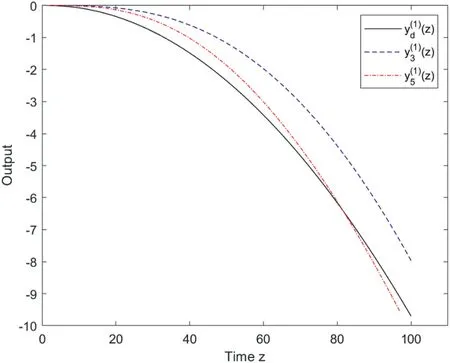
F I G U R E 1 0 (case 1 of Example 2): The resulting output trajectory yk(z) to the desired output trajectory yd(z) at iterations k=3 and k=5.

F I G U R E 9 (case 1 of Example 2): The profiles of ILC tracking error index SEk versus iteration k.

F I G U R E 1 1 (Case 2 of Example 2):The profiles of iterative initial states,(i=1,2)as tThevalues of initial state satisfiesE｛‖xd(0)-xk(0)‖｝≤δwithxd(0)= [0 0]andδ=0.08.

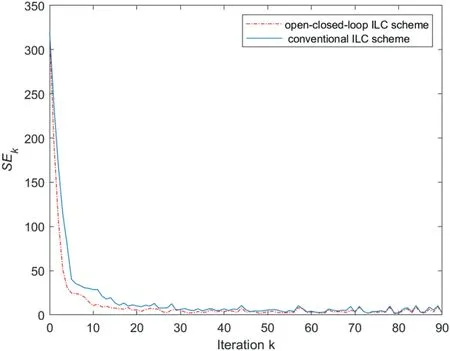
F I G U R E 1 2 (Case 2 of Example 2): The profiles of ILC tracking error index SEk versus iteration k.

F I G U R E 1 3 (Case 2 of Example 2): The resulting output trajectory yk(z) to the desired output trajectory yd(z) at iterations k=3 and k=5.

6 | CONCLUSION

In this article, an iteration dependent interval based openclosed-loop ILC algorithm is developed for LTV MIMO systems with vector relative degree, in which the initial state can vibrate around the desired one with identical expectation.Theoretical analysis and simulation results have demonstrated that as the iteration number tends to infinity,the mathematical expectation of ILC tacking error can be controlled to zero beyond the initial time points, which depends on the vector relative degree of controlled system.Under initial state fluctuation, as the number of iteration tends to infinity, the proposed iteration dependent interval based open-closed-loop ILC law can drive the expectation of ILC tracking error to a bounded range, whose upper bound is proportional to the fluctuation.For the systems with integrated high relative degree, a simplified ILC law is given under these two initial conditions.It is shown that the convergence condition is determined by the feedforward gains, while the proper feedback control gains can expedite the convergence speed.Further works can focus on extending the developed openclosed-loop ILC approach to networked dynamical systems or non-repetitive systems.

ACKNOWLEDGEMENTS

This work was supported in part by the National Natural Science Foundation of China of No.61903096, Guangzhou Key Laboratory of Software-Defined Low Latency Network of No.202102100006, and Guangdong Basic and Applied Basic Research Foundation of No.2020A1515110414.

CONFLICT OF INTEREST STATEMENT

None.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.

ORCID

Yun-Shan Weihttps://orcid.org/0000-0002-2949-9517

Qing-Yuan Xuhttps://orcid.org/0000-0002-4511-6838