斯小琴,陈大伟,岳生伟

(1.安徽建筑大学 城市建设学院,合肥 238076;2.中国科学技术大学 物理学院,合肥 230026)

热传导(thermal conduction)实质是由于物体内部大量分子热运动相撞击使温度分布不均匀,即物体内存在温度差,热量要从物体温度较高的点流向温度较低的点[1-2]。热传导过程是一个基础性的物理过程,其数学模型在实际应用中非常广泛[3-7],如光学研究、航天科学技术、地质勘测、水利工程、工业制造等诸多领域。因此,对热传导的研究越来越受到人们的重视。

热传导过程通常用偏微分方程表示,借助数学模型来描述物体上各点的温度分布和变化具有重要的意义。对这种偏微分方程进行研究有助于对热传导过程基本规律的更深理解,以便用来更好的解决实际问题[8-9]。而对于各种定解条件下的热传导方程的求解更是一个热点问题。虽然科研工作者们已经提出了一些求解其解析解的方法[10-12],但这些获得的解只对少量的简单情形适用,对于那些具有实际物理意义的复杂的热传导问题,其精确解往往很难得到,这时使用数值解方法来求解就显得尤为重要[13-14]。

求解热传导问题数值解方法很多,最常用的方法有有限差分法、有限元法和边界元法。差分法[15]划分的网格是规则的,具有形式简单、使用方便的优点,但对计算条件要求高;有限元法[16]网格划分则较灵活,对于不规则区域和弯曲边界可方便的处理,但需要求解大规模线性代数方程,这将消耗过长的计算时间和占用较大的CPU存储空间;边界元法[17]用简单的网格准确模拟边界形状,得到线性代数方程组的阶数较低,具有较高的精度,但难以应用于非均匀介质问题。

本文利用最常用的较成熟、应用广的有限差分法,借助基本办公软件Excel迭代[18-19],通过Origin将迭代的数据模拟成图形,得到了含初始和边界条件的混合问题的一维热传导方程的温度随时空变化图,以及数值解与精确解的误差比较。从图像中观察物体上各点的温度随时间和空间的分布状态。将简单、灵活、精度高、通用性强的有限差分法与基本办公软件Excel的迭代计算功能相结合,避免了求解繁琐的热传导方程以及复杂的计算机编程,给解决实际问题带来了方便。进一步通过Origin将数值模拟成图形,结果直观、形象。

1 模型与方法

长度为1 m的匀质热导体,其两端的温度均为0 ℃且保持温度不变,初始时刻温度分布为u(x,0)=sinπx,考察该热导体上温度的分布情况。则其热传导方程表示如下:

(1)

其中u(x,t)表示导热体上t时刻x处的温度,该方程的精确解为

u(x,t)=e′-π2tsinπx

通过有限差分法求方程(1)的数值解。现将温度u(x,t)在节点(x,t)处沿x向前h、向后h以及沿t向前τ进行Taylor展开,有

(2)

(3)

(4)

由式(2)+(3)并略去高阶项,得

(5)

由式(4)略去高阶项,得

(6)

将式(5)(6)代入式(1),有

(7)

以时间步长τ=0.15/m和空间步长h=1/n(m,n为自然数)分别将时间[0,0.15]和空间[0,1]进行离散化,可以将一维的时空平面划分成一个m×n的网格面,各个网格点则表示所对应的时空温度。得到式(1)热传导问题的离散网格分别表示如下:

(8)

则由式(7)可得一维差分方程为

(9)

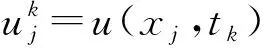
引入步长比r=τ/h2,则式(9)可改写为

(10)

2 数值模拟结果及分析

现取不同的步长,考察τ和h取值不同,其对数值解精度高低的影响。在基本办公软件Excel中第一行表示空间节点,第一列表示时间节点,分别代入式(1)中的初始和边界条件,再编入式(10)的差分公式,利用其迭代计算很快计算出各时刻在每个位置的温度值。改变步长,温度值随之改变。将得到的数值解与精确解进行比较,计算出两解差的绝对值,通过MAX函数得到其最大误差。表1列出了部分最大误差数值,固定空间步长h=0.05 m不变,改变时间步长。步长改变,其步长比r紧跟改变,从表1中可以看出,步长比越小,数值解的精度越高,也就是说,所取得步长越小,精度越高,这些前提是要步长比r≤1/2。

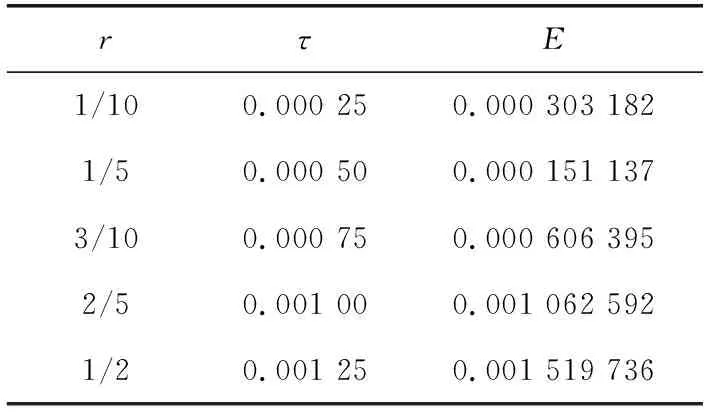
表1 不同步长比时数值解的最大误差

下面在此方法稳定的条件下以最大步长比即r=1/2讨论相关问题。若分别取空间步长h=0.05和时间步长τ=0.001 25,通过Excel计算出数值解和精确解数值及两解差的绝对值。表2 列出了其数值解、精确解及两解差的绝对值在部分节点处的数值。

表2 部分节点处数值解、精确解及两种解的差的绝对值

为了直观、形象地观察和理解热导体上热量分布随时间、空间的变化规律,通过Origin画图软件将计算出的数值模拟成图形。图1是h=0.05和τ=0.001 25的温度随时间和空间变化的数值解图。从图1中很直观地看出,在x=0时温度为0 ℃,随着位置的变化,温度先增大随后减小,直到导热体的另一端温度又减小到0 ℃,即该端点处与外界绝热,图形与理论基本相吻合,从图形中观察更直观。

图1 导热体上的温度随时间、空间变化分布

通过数值解与精确解进行对比,更好地说明了此方法在精度范围内的可行性。图2是数值解和精确解误差曲面图。从图2中可看出,误差值很小,基本都在0.001即0.1%之内。沿着x方向向前看,误差值先增后减;沿着t方向向前看,误差值先急剧增加后趋于平缓。

图2 数值解与精确解误差曲面

图3和图4是图2的剖析图,分别考察了误差值与位置x和时间t的关系。图3是取空间步长h=0.05和时间步长τ=0.001 25,当位置控制在x=0.6 m时的误差随时间变化的曲线。从图3中可以看出,开始时误差增加的较大而后趋于平缓甚至最后有减小的趋势,与图2中观察到的基本一致。

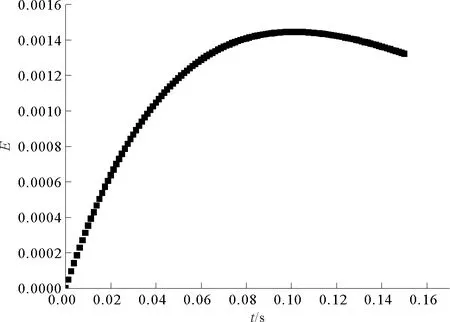
图3 误差随时间变化的曲线

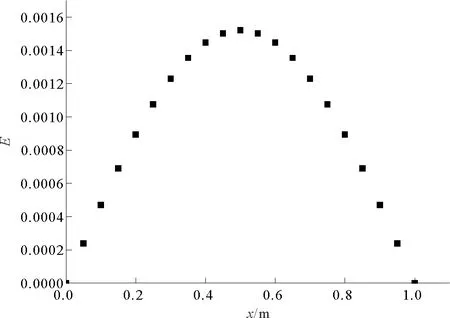
图4 误差随空间位置变化的曲线

图4是取空间步长h=0.05和时间步长τ=0.001 25,当时间控制在t=0.1 s时的误差随空间位置变化的曲线。从图4中可知,在两端点处因都保持0 ℃不变,误差值均为0,随后误差值先增加后减小,出现对称分布状态,与图2中的相吻合。

3 结论

本文通过有限差分法的差分格式得到了一维热传导方程的数值解,将其初始、边界条件及数值解的差分格公式编入基本办公软件Excel中,通过其下拉迭代计算功能,快速地得到了热传导方程每个网格点的温度值。借助Origin将计算出的大量数据绘制成图,并与精确解进行对比,得到了数值解与精确解的误差曲面图。从图形中观察结果更加直观、形象。该方法对于不同初始、边界条件下或有非齐次项f(x,t)的热传导方程的求解同样适用。对解决实际问题带来了方便并有一定的参考价值。