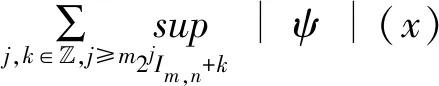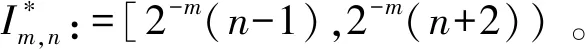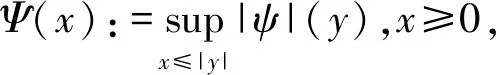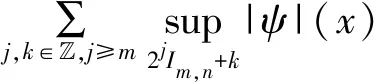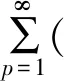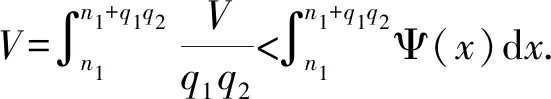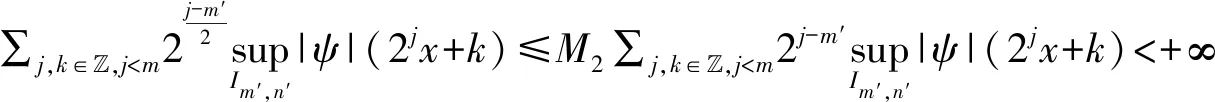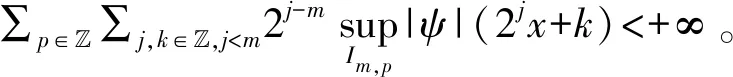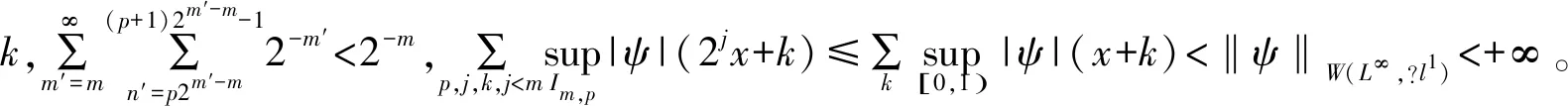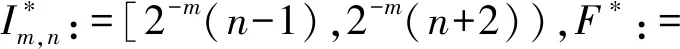紧支撑小波在Lebesgue空间中的表现
2023-10-11王凯城
王凯城
(三明学院 信息工程学院,福建 三明 365004)
Lebesgue空间中小波基底的完备性与描述,一般使用两种方法之间:使用Calderón-Zygmund算子(CZO)和使用Calderón-Zygmund分解定理(CZD)。一方面,使用CZO是通过提供平滑度和众所周知的定理来使某些算子获得LP有界的一种方法。这种获得LP有界的方法被广泛使用。至于小波基的取得,2016年宋亮等[1]多尺度多重解析构建双正交小波,须求条件为有限频率与时间域平滑性。张静等[2]使用双向细分方程与双向小波,对多尺度函数的逼近阶作了介绍。陈清江等[3]构造多尺度双向向量值小波,须求条件为小波须为紧支撑。
Kumar[4-7]在2009—2014年间,发表一系列的特定小波诠释算子的有界性的文章,专门介绍空间的紧致性与算子的有界性,藉由成熟的CZO技术,取得相当多的成果。可是,使用CZO,不可避免小波必定要有平滑性。而相关算子的有界性,需要具备平滑性条件取得,更遑论空间的紧致性的取得。
本文的目的并不着重在于小波基底的取得,而是对于一群特殊的小波基底——紧致小波正交基底,使用CZD,说明他们在Lebesgue空间中具有完备性。 并且不需要额外具备其他的条件。
1 基本背景和符号
定理1在Banach空间中给定序列{xn}。 以下是等价的。
(a)∑xn无条件收敛;
(c)∑λnxn对于标量{λn}的每个有界序列收敛。
可测函数f属于W(L∞,l1),如果满足
导致并将f∈Lp(),对于所有 1≤p≤∞
令Q是从映射LP()到Lq(),对于所有1≤p,q≤+∞。那么Q的类型为(p,q),如果‖Q(f)‖q≤A‖f‖p,f∈Lp(),其中,A不依于f。同样,Q是弱类型(p,q),如果
其中,A不依于f或α; 而m是Lebesgue测度。注意到(p,q)类型的运算也是弱(p,q)。更多详细资讯可在参考文献[8]中找到。
称{ψi:i∈}为L2()的框架,如果存在两个常数使得
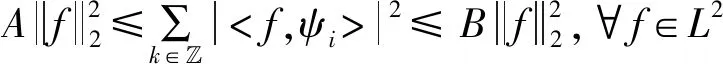
如果A=B,称这是一个紧框架(tight frame)。请注意框架不一定线性无关。
定义的{ψi:i∈}框架算子S为
其中的每一个f∈L2()皆可分解成
该序列在L2()中无条件收敛。 {S′ψi:i∈}被称为{ψi:i∈}的规范对偶,而每一个框架都有自己的规范对偶。T称为{ψi:i∈}的预框架,被定义为
T:l2()→L2(),
S和S-1是类型(2,2),有界的,自伴,正定,并且可逆在L2()。}也是L2()中的一个框架。 紧框架的规范对偶}为}。 在L2()的正交基底即为紧框架在L2()。
接下来转向小波(wavelet)。在本文中,使用以下符号
ψj,k(x):=DjTkψ(x)=2j/2ψ(2jx+k)。
其中,Dj(·)(x):=2j/2(·)(2jx),Tk(·)(x):=(·)(x+k).在L2(),由ψ生成的仿射小波框架系统定义为{ψj,k:j,k∈},也是L2()的框架。 在L2()的仿射小波正交基底即为紧框架在L2()。 特别的是,仿射小波正交基底需要具备线性无关,并且其规范对偶与原正交基底结构一致。
相关于本文中,小波上的限制有以下几点,需要注意。 一般来说,小波函数ψ须属于L2(),并且ʃψ=0。 紧支撑的小波不可能符合无穷多次可导。
2 结果及其证明
以下是CZD与目标算子特殊的设计。对于所有f∈L1∩L2()和α>0,存在一个集合Ω⊂2,这样间隔{Im,n}(m,n)∈Ω不相交,Im,n:=[2-mn,2-m(n+1)),|f(x)|≤α,对于几乎所有F:=∪(m,n)∈ΩIm,n,以及所有(m,n)∈Ω中,α<2mʃIm,n|f|≤ 2α。因此,∑(m,n)∈Ωα2-m<‖f‖1。
设Fψ:={ψj,k:j,k∈}是仿射紧支撑(compactly supported)小波正交基底系统,并且因为Fψ正交在L2(),所以<ψj′,k′,ψj,k>:=ʃψj′,k′ψj,k=δj′,k′;j,k。定义仿射运算子Q(·):=∑j,k∈θj,k<·,ψj,k>ψj,k,其中Θ:={θj,k:j,k∈}∈l∞。
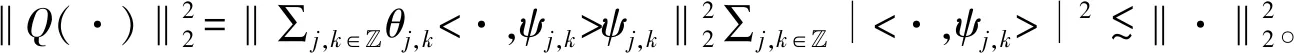
一旦Q的Lp有界取得,便可取得小波基底在Lp(),1 实际上,由于L2∩Lp()是Lp(),1 用Pm表示从L2()到子空间,j 以下,将要介绍定理2,是本文主要结果的基础。 定理2给定仿射紧支撑小波正交基底系统Fψ:={ψj,k:j,k∈},以下会成立,并且有限的取得与m,n无关。 证明: 上式有限的取得是来自于ψ是紧支撑的。 其次有, 而上式有限的取得是来自于下式有限的取得与Dirichlet检定。 确实的,将使用反证法来说明。 给定V>0, 存在j0>m,k0∈,q1,q2∈使得 其中,j1∈{j0,j0+1, …,j0+q1-1},k1∈{k0,k0+1, …,k0+q2-1}。 并且也存在x0与n0∈,x0∈[k1,k1+2j1-m)使得 接下来,将会证明定理3,这说明算子Q具备Lp有界。相较于文献[9-10],没有复杂的证明程序,也不需要任何衰退或平滑的条件。 定理3给定仿射紧支撑小波正交基底系统Fψ:={ψj,k:j,k∈}.则,对于1 证明:本证明最主要是要证明Q为弱(1,1)类型。 确实的,先前已说明Q为(2,2)类型,一旦说明Q为弱(1,1)类型,根据Marcinkiewicz拓补定理,Q为(p,p),1 如果取得上述二不等式的成立,则有 m{x:|Qf|>α}≤m{x:|Qg|>α/2}+m{x:|Qh|>α/2} Q即为弱(1,1)类型。 首先证明,根据定理2 与Dirichlet检定,对于任何(m,n),(m′,n′)∈Ω,m≤m′,以下M1,M2,M3均为定值,并且有限的取得与m,n无关 紧接着,ʃ|fχF|2≤αʃF|f|≤α‖f‖1.故, 再证, 最后,请注意m{故