■河南省郑州市第四高级中学 李 亚

题型一 利用向量法证明空间的平行和垂直关系

例1(2021年全国甲卷理数)如图1,已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,|AB|=|BC|=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点。BF⊥A1B1。

图1

(1)证明:BF⊥DE;

(2)当|B1D|为何值时,平面BB1C1C与平面DFE所成的二面角的正弦值最小?

分析：第一问,用常规方法证明较为复杂,建立合适的空间直角坐标系,借助空间向量求解非常简捷。第二问,利用空间向量求二面角的平面角是最常规的方法,也是最优方法。

解：(1)因为三棱柱ABC-A1B1C1是直三棱柱,所以BB1⊥底面ABC,且BB1⊥AB。

因为A1B1//AB,BF⊥A1B1,所以BF⊥AB。

又BB1∩BF=B,故AB⊥平面BCC1B1。

所以BA,BC,BB1两两垂直。

以B为坐标原点,分别以BA,BC,BB1所在直线为x轴,y轴,z轴 建 立空间直角坐标系,如图2。

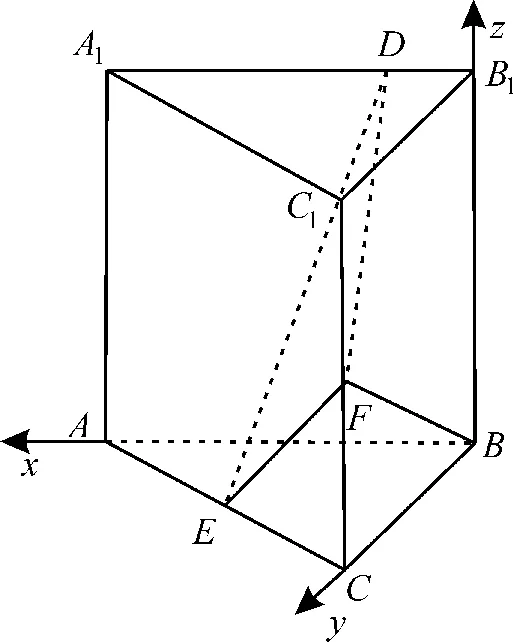
图2

则B(0,0,0),A(2,0,0),C(0,2,0),B1(0,0,2),C1(0,2,2),E(1,1,0),F(0,2,1)。

由题意设D(a,0,2)(0≤a≤2)。令z=2-a,则m=(3,1+a,2-a)。

题型二 利用向量法求异面直线所成角

例2在直三棱柱ABC-A1B1C1中,△ABC是 等 腰 直 角 三 角 形,,P是 线 段A1B1上的动点,则当线段CP最短时,异面直线AC1与BP所成角的余弦值为( )。

解析：在直三棱柱ABC-A1B1C1中,△ABC是等腰直角三角形,所以,

以点C为坐标原点,以CA,CB,CC1所在直线分别为x轴,y轴,z轴,建立图3 所示的空间直角坐标系。

则A(2,0,0),B(0,2,0),C(0,0,0),A1(2,0,4),B1(0,2,4),C1(0,0,4)。

因此,当线段CP最短时,异面直线AC1与BP所成角的余弦值为,选A。

题型三 利用向量法解决线面角问题

例3(2022年全国甲卷理数)如图4,四棱锥P-ABCD中,PD⊥底面ABCD,CD//AB,|AD|=|DC|=|CB|=1,|AB|=2,|DP|=。

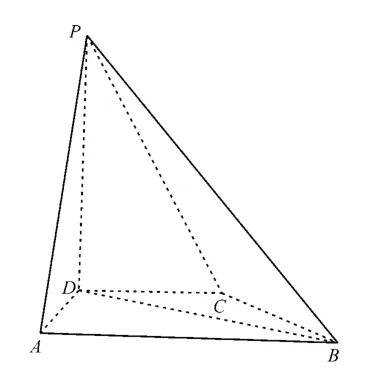
图4

(1)证明:BD⊥PA;

(2)求PD与平面PAB所成角的正弦值。

分析：(1)作DE⊥AB于E,CF⊥AB于F,利用勾股定理证明AD⊥BD,根据线面垂直的性质可得PD⊥BD,从而可得BD⊥平面PAD,再根据线面垂直的性质即可得证;

(2)以点D为原点建立空间直角坐标系,利用向量法即可得出答案。

解：(1)解题过程略。

(2)如图5,以点D为原点,以DA,DB,DP为x轴,y轴,z轴建立空间直角坐标系。

图5

题型四 利用向量法解决二面角问题

例4(2023年新课标Ⅰ卷)如图6,在正四棱柱ABCD-A1B1C1D1中,|AB|=2,|AA1|=4。点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,|AA2|=1,|BB2|=|DD2|=2,|CC2|=3。

图6

(1)证明:B2C2//A2D2;

(2)点P在棱BB1上,当二面角PA2C2-D2为150°时,求|B2P|的值。

分析：(1)建立空间直角坐标系,利用向量坐标相等证明;(2)设P(0,2,λ)(0≤λ≤4),利用向量法求二面角,建立方程求出λ即可得解。此题一改以往直接求解二面角的相关问题,明显对逆向思维能力的考查有所提升,重点考查同学们的逻辑推理能力。

解：(1)以C为坐标原点,分别以CD,CB,CC1所 在 直 线 为x轴,y轴,z轴,建 立空间直角坐标系,如图7。

图7

则C(0,0,0),C2(0,0,3),B2(0,2,2),D2(2,0,2),A2(2,2,1)。

化简可得λ2-4λ+3=0,解得λ=1或λ=3,故P(0,2,1)或P(0,2,3),|B2P|=1。

题型五 利用向量法求点到直线的距离

例5如图8,在平行六面体ABCDA1B1C1D1中,以顶点A为端点的三条棱长都是a,且AB⊥AD,∠A1AB=∠A1AD=60°,E为CC1的中点,则点E到直线AC1的距离为( )。

图8

题型六 利用向量法求异面直线的距离

例6如图9,在三棱柱ABC-A1B1C1中,底面△ABC是边长为的正三角形,|AA1|=,顶点A1在底面的射影为△ABC的中心,P,Q分别是异面直线AC1,A1B上的动点,则P,Q两点间距离的最小值是( )。

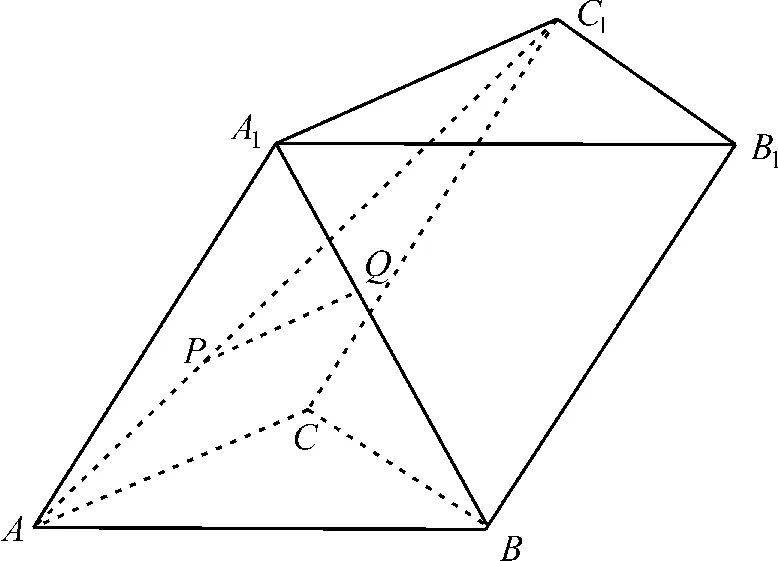
图9

分析：建立空间直角坐标系,P,Q两点间距离的最小值即为异面直线AC1与A1B间的距离。

解：如图10,O是△ABC的中心,A1O⊥平面ABC,AO⊂平面ABC,故A1O⊥AO。

|AB|=2,则,则

故选D。

题型七 利用向量法求点到平面的距离

例7如图11,在四棱锥P-ABCD中,底面ABCD为平行四边形,侧面PAD是边长为2的正三角形,平面PAD⊥平面ABCD,且AB⊥PD。

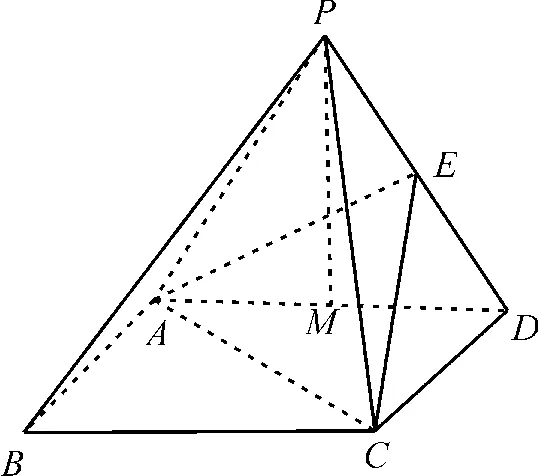
图11

(1)求证:平行四边形ABCD为矩形;

(2)若E为侧棱PD的中点,且平面ACE与平面ABP所成角的余弦值为,求点B到平面ACE的距离。

分析：(1)取AD中点M,连接PM,由正三角形、面面垂直的性质易得PM⊥平面ABCD,再由线面垂直的性质及判定定理证AB⊥AD,即可得结论;(2)构建空间直角坐标系,设|AB|=t＞0,并求平面ACE、平面ABP的法向量,结合面面角的余弦值求参数,应用向量法求点面距。

解：(1)证明过程略。

(2)如图12,以A为原点,AB所在直线为x轴,AD所在直线为y轴,建立空间直角坐标系,设|AB|=t＞0,则A(0,0,0),B(t,0,0),C(t,2,0),P(0,1。

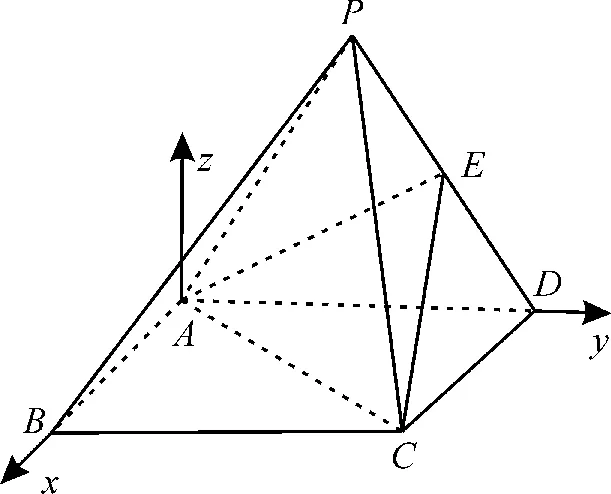
图12