西华师范大学数学与信息学院 李佳洁 赖周萍

罗增儒教授认为“数学教育中真正发生数学的地方都无一例外地有数学解题活动”.在数学教学中,“一题多解”是一种最常用、最有效的教学手段.通过“一题多解”从不同角度对问题结构展开分析,将已有的数学知识输出,经历观察、猜测、证明的过程,培养学生的发散性思维[1].本文中将从一道例题的多种解法出发,逐步培养学生的发散性思维.

例题若a,b均大于1,且满足ab=a+b+3,求ab的最小值.

1 利用均值不等式

方法一：因为ab=a+b+3,所以a+b=ab-3.

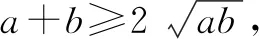
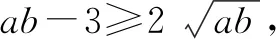
所以ab≥9.

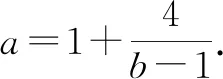
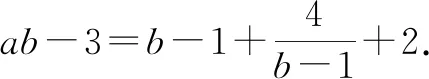
故ab≥9.

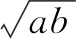
2 利用根与系数的关系

方法三：构造对偶式.

因为ab=a+b+3,所以构造ab+(a+b)=t.

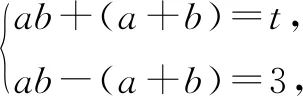
基于一元二次方程根与系数的关系,可以将a,b看作一元二次方程Ax2+Bx+C=0两根,则

此时,原一元二次方程可以写为

2x2-(t-3)x+3+t=0.

因为该一元二次方程有两实根,所以△≥0,即(t-3)2-8(3+t)≥0.

化简,得(t-15)(t+1)≥0.

由于a,b是大于1的正数,因此t>1.

故t≥15,即ab≥9.

方法四：直接设值.

由于ab=a+b+3,不妨设ab=t,则a+b=t-3.

根据一元二次方程根与系数的关系,可以将a,b看作一元二次方程Ax2+Bx+C=0的两根,则

此时,原一元二次方程可以写为

x2-(t-3)x+t=0.

因为方程有两实根,所以Δ≥0,即(t-3)2-4t≥0.

化简为(t-9)(t-1)≥0.

由于a,b是大于1的正数,因此t>1.

故t≥9,即ab≥9.

点评：以上两种方法在于细致的观察,等式中出现的变量有ab和a+b,基于这两种形式的特殊性,联想到一元二次方程中根与系数的关系,再运用判别式求ab的范围.方法三在解题过程上会略显复杂,运用对偶法解决出现ab和a+b两种形式的题较为常见.

3 利用数形结合思想

方法五：几何法——等面积法.

如图1,长方形ABCD中,AB=a,BC=b.

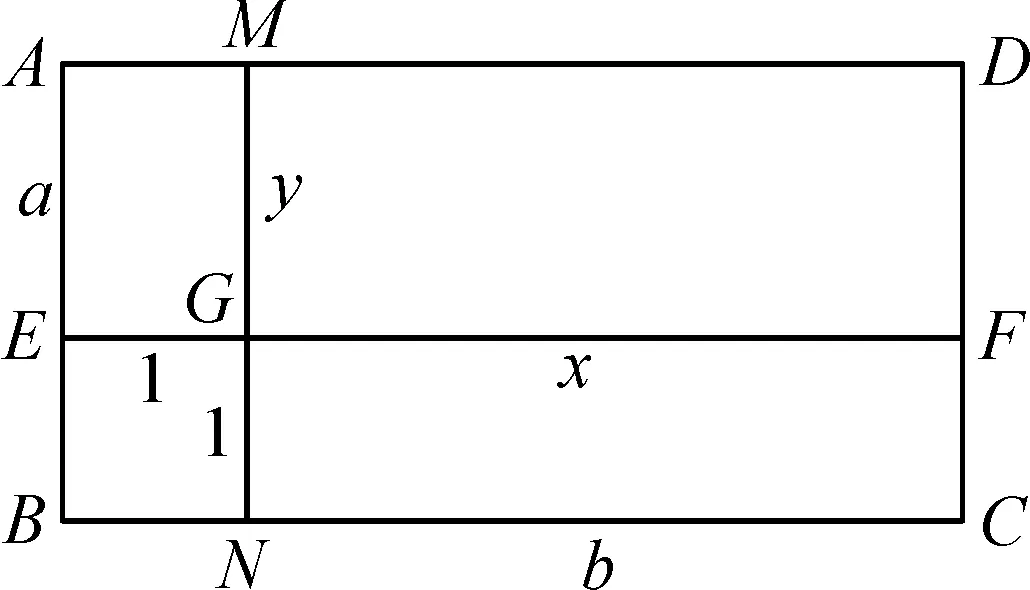
图1

在AB上取一点E,令BE=1,过点E作AB的垂线交DC于点F;在BC上取一点N,令BN=1,过点N作BC的垂线交AD于点M.

令GF=x,MG=y,则有a=y+1,b=x+1.

即y=a-1,x=b-1.

由图可知S矩形ABCD=ab,且有

S矩形ABCD=S矩形AEGM+S矩形BEGN+S矩形GNCF+S矩形MGFD

=y+1+x+xy

=a+b+(a-1)(b-1)-1.

又ab=a+b+3,所以(a-1)(b-1)=4.

即SMGFD=xy=4.

当xy的值确定,要求x+y的最小值,即求长方形MGFD的周长的最小值,而矩形面积一定时,正方形周长最小.

故当且仅当x=y=2时,x+y最小.此时,a=b=3,ab的最小值为9.

点评：该解法尝试将代数问题转化为几何问题,使问题更加形象、具体.通过构建长方形,借助面积法表示出ab,(a-1)(b-1),并基于图形的几何意义找到二者的代数关系.为了求最小值,将面积问题转化为周长问题进行解决.数形结合法拓展了学生思考问题的维度,促使学生进入更高阶的思维层次.

4 利用数列知识

方法六：等差数列法.

因为ab=a+b+3,所以ab-3=a+b.

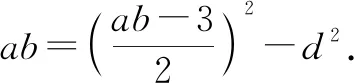
(ab-9)(ab-1)≥0.

由于a,b是大于1的正数,因此ab≥9.

方法七：等比数列法.

由ab=a+b+3,得(a-1)(b-1)=4.

由a,b是大于1的正数,可知q>0.

点评：方法六和方法七均先对等式进行变形,将视角聚焦到变式后的结构形式上.通过将该等式割裂成三项,建立了等式与特殊的函数——数列之间的联系,将等式分割为三项,从数列的等差、等比中项的性质出发,建立关系,从而求出ab的范围.该方法对学生基础知识和思维能力的要求较高.

本文中对一道例题进行“一题多解”,从多角度思考数学问题.除了常用的解题方法,还尝试从新的视点分析问题,建立初高中所学习知识体系的联系.例如,将代数问题转化为几何问题,借助图象用面积法解决问题;将代数与特殊的函数——数列建立关系,利用数列的性质解决问题;等等.这样的转化,可将“摸不透”的问题“明晰化”,使学生对所学知识做到融会贯通,实现思维层次的高阶化[2].