周 胥

(广东省深圳市布吉高级中学)

纵览历年高考,三次函数问题的考查力度逐年增大.在高次函数家族里,三次函数虽然最简单,但当三次函数问题中含有参数或与其他知识综合考查时,它的难度就上升了,因此很有必要对三次函数问题的求解策略进行研究.笔者认为,求解含参三次函数问题要有四种意识,即方程意识、数形结合意识、分类讨论意识和等价转化意识,本文将依次举例说明.

1 方程意识

求参数的值,一般采用待定系数法,通过解方程解决.对于含参数的三次函数解析式,要确定参数的值,可以根据题设条件列方程或方程组.

例1已知函数f(x)＝2x3＋ax2＋bx＋1的极值点为－1和1,求函数f(x)的解析式.

分析根据导数与极值点的关系列方程或方程组求解得出a,b的值,由此得出解析式.

解易求出f(x)的导数f′(x)＝6x2＋2ax＋b,因为f(x)的极值点为－1和1,所以

点评

本例中的三次函数有两个待求参数,所以可建立方程组求解.这类问题难度不大,主要考查函数极值的意义.

2 数形结合意识

利用导数知识,很容易作出三次函数的图像.三次函数的导数是二次函数,它的图像也容易作出.我们可以利用它们图像之间的关系找到三次函数问题的解题思路.

例2已知函数有两个极值点x1,x2,若f(x1)＝x1＜x2,则关于x的方程[f(x)]2＋bf(x)＋c＝0的不相等的实根个数为( ).

A.2 B.3 C.4 D.5

分析对函数进行求导,将函数的两个极值点x1,x2转化为f′(x)＝0 的两个根,即可推出关于f(x)的方程[f(x)]2＋bf(x)＋c＝0 的两个根为f(x)＝x1或x2.若f(x1)＝x1＜x2,由导函数图像,判断函数的单调性,并画出函数图像,由图像即可求出方程[f(x)]2＋bf(x)＋c＝0不同的实根.

解因为f′(x)＝x2＋bx＋c,由题意知x1,x2是函数f(x)的两个极值点,即x1,x2是方程x2＋bx＋c＝0 的两个根,从而关于f(x)的方程[f(x)]2＋bf(x)＋c＝0有两个根,f(x)＝x1或x2.

若f(x1)＝x1＜x2,则根据题意可画出函数f′(x)和f(x)的图像,如图1、图2所示.

一阵凉风透过窗户缝隙吹进来，把紧闭着的卫生间窗帘掀开了一条缝。她一惊，伸手要去拉拢来。可就在她的手触到窗帘的刹那间，她的目光无意间投向了窗外，她看到了一个令人心跳耳热的镜头。对面一间房子的窗户，窗口的大红双喜还未褪色，不知是疏忽，还是过于急切，那对年轻夫妻未拉上窗帘也未关灯就除去彼此的衣物，赤裸地滚落床第，两具肉体像柔软的藤条般缠绕在一起，似乎憋足了半个世纪的爱和欲要在这一刻尽情地倾泻……

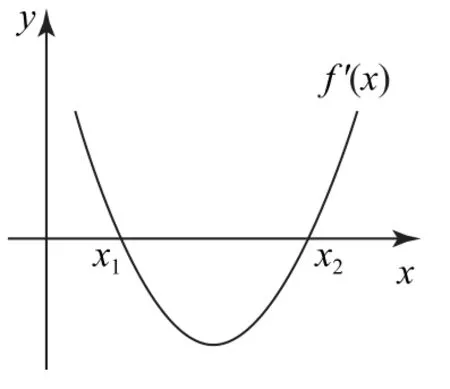
图1

图2

由图可看出f(x)＝x1有两个不相等的实根,f(x)＝x2只有一个实根.

综上,方程[f(x)]2＋bf(x)＋c＝0的不相等的实根个数为3个,故选B.

点评

上面的解法借助数形结合揭示了三次函数图像及其导函数的图像之间的关系,解题过程既直观,又清晰.

3 分类讨论意识

当含参数的三次函数问题要求某个参量的取值范围时,一般需分类讨论,尤其是函数单调性与极值的讨论,是常考题型.

例3若函数f(x)＝(x＋2)2(x－a)的极小值小于0,则实数a的取值范围为_______.

分析根据导数的性质,结合导函数零点的大小关系、极小值的定义分类讨论进行求解即可.

点评

根据导函数f′(x)零点的大小进行分类讨论是解答本题的关键.在许多研究函数性质的问题中,我们常常利用不等式作为解题的工具.求函数的单调区间,对应着解相应的不等式;求参数的取值范围,对应着研究不等式恒成立问题,于是通常把原问题转化为含参不等式问题,因此解题时要有分类讨论意识.

4 等价转换意识

求解含参三次函数问题,通常可通过求导将原问题转化成二次问题(包括二次函数、二次方程和二次不等式),最常见的是方程有解问题和不等式恒成立问题.

例4(1)已知没有极值,则实数a的取值范围是( ).

A.(0,1) B.(－∞,0)∪(1,＋∞)

C.[0,2] D.(－∞,0]∪[2,＋∞)

(2)已知f(x)＝x3－x,如果过点(2,m)可作曲线y＝f(x)的3条切线,则m的取值范围是_______.

分析(1)根据导数与函数极值的关系可知f′(x)≥0或f′(x)≤0恒成立,再结合二次函数的性质即可求解本题.(2)由导数法可得过(t,f(t))的切线方程为y＝(3t2－1)x－2t3,由过点(2,m)可作曲线y＝f(x)的3条切线得m＝－2t3＋6t2－2有3个不相等的实根,令g(t)＝2t3－6t2＋2＋m,由导数法讨论函数的单调性与极值,根据数形结合得出范围即可.

解(1)因为所以f′(x)＝x2＋2(a－1)x＋1.

因为f(x)没有极值,所以f′(x)≥0或f′(x)≤0恒成立.又因为f′(x)的开口向上,所以f′(x)≥0恒成立,即Δ≤0,所以[2(a－1)]2－4≤0,整理得a2－2a≤0,解得0≤a≤2,所以a∈[0,2],故选C.

(2)f′(x)＝3x2－1,则过(t,f(t))的切线为yf(t)＝f′(t)(x－t),即y＝(3t2－1)x－2t3.由过点(2,m)可作曲线y＝f(x)的 三条切线,得m＝－2t3＋6t2－2有3个不相等的实根.

令g(t)＝2t3－6t2＋2＋m,则g′(t)＝6t2－12t,由g′(t)＝0,得t＝0或2.

当t＜0或t＞2,g′(t)＞0,g(t)单调递增;当0＜t＜2,g′(t)＜0,g(t)单调递减,故当t＝0 时,函数g(t)取得极大值2＋m;当t＝2时,函数g(t)取得极小值m－6.要使g(t)＝0 有3 个不相等的实根,则－2＜m＜6,即m的取值范围是(－2,6).

点评

第(1)问中的函数f(x)没有极值,可等价转化为该函数单调,即f′(x)≥0或f′(x)≤0,于是转化为不等式恒成立问题;第(2)问中过一定点作出曲线的三条切线很难理解,更不容易正确使用该条件,往往会使思维陷入误区,但合理地将存在三条切线问题转化为方程存在3个不相等的实根问题,降低了问题难度,体现了转化的重要作用.

数学解题,思想方法先行.以上四种意识,也是破解三次函数问题基本的思想方法.

(完)