陈艺夫，马宇航，蓝庆生，孙卫平，史亚云，杨体浩，*，白俊强

1．西北工业大学 航空学院，西安 710072

2．中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

3．中航通飞华南飞机工业有限公司，珠海 519000

4．西安交通大学 航空学院，西安 710049

所有工程系统的性能都会受到某种程度不确定性的影响。由于受到加工制造或飞行条件及环境等诸多不确定性因素的影响，飞行器的性能容易出现较大变化。传统的气动设计属于确定性设计，有可能导致气动性能对不确定因素异常敏感，甚至会带来一定的安全隐患。因此，在飞行器设计阶段，关注不确定因素对飞行器性能的影响显得尤为重要。

美国NASA 于1998年对工程上多学科设计领域的需求进行了调查［1］，调查结果表明，需要提高飞机在多种不确定性因素下的不确定性能。2002年，NASA 又推出了有关航空航天领域不确定性下多学科优化设计的规划［2］，规划中明确指出了飞行器不确定性下设计的难点和挑战，为未来一段时间内的研究奠定了基础。规划推出后，NASA 兰利研究中心致力于对跨声速翼型进行不确定性优化设计。从Huyse［3］和Walters［4］等对二维翼型考虑马赫数不确定性的优化设计研究中，可以看出确定性优化和不确定性优化之间存在较大差异，进一步说明了在翼型设计中考虑不确定性影响的重要性。

为开展考虑不确定性的鲁棒优化设计，首先需要建立高效精确的不确定性分析方法。在不确定性分析中，很重要的一步是将不确定源的特征转化为输出变量（Quantity of Interest，QoI）不确定性估计的过程，称之为不确定性的传播。不确定性传播方法可分为4 大类：解析法［5］、取样法［6］、随机响应面模型法和代理模型法。

现代气动设计大量依赖于使用CFD 工具来预测所考虑的气动外形的性能，在减少了昂贵的风洞试验的同时，效率因此得到显著提升，设计周期进一步缩短。Pelletier［7］和Luckring［8］等在其研究中阐述了CFD 模拟中不确定性的来源和分类。Walters 等［4］总结了针对CFD 中不确定性的分析方法。Schaefer 等［9］在其最新的综述类文章中对当前航空航天领域CFD 模拟的不确定性分析方法进行了总结。Roelofs等［10］在其文章中总结了在不确定性条件下所进行的优化设计研究工作，重点关注的是分配和量化这些不确定性的方法和建模方法。研究发现，概率方法仍然是表示不确定性的最流行理论。多项式混沌展开法和随机配置方法越来越受欢迎，但蒙特卡洛模拟仍被广泛使用。

近年来，多项式混沌法在CFD 气动设计不确定性分析中的应用最为广泛。Knio 等［11］和Najm［12］在其综述中总结了多项式混沌法在CFD不确定性分析中的发展和应用现状。国内外学者采用多项式混沌法对CFD 气动设计中的不确定性问题开展了大量研究工作。基于非嵌入式多项式混沌法，Loeven 等［13］研究了一维活塞问题和二维亚声速翼型的不确定性问题。Simon［14］和Chassaing［15］等对二维翼型跨声速下马赫数和迎角的不确定影响进行研究，敏感性分析表明，不确定参数之间存在很强的非线性耦合。Yamazaki［16］则利用阻力分解方法分析了二维翼型的不确定性量化问题。在Suga 等［17］的研究中，多项式混沌方法被用于二维超声速双翼飞机翼型的气动不确定性量化。Hosder 等［18］分别对膨胀波拐角角度的几何不确定性和跨声速三维机翼的马赫数、迎角不确定性开展了研究。West 等［19］开发了一种多保真多项式混沌法，并将其成功应用于超声速客机的不确定性分析问题中。

在内流研究中该方法也已得到了广泛应用。Ghisu［20］、Abraham［21］和Li［22］等利用非嵌入式多项式混沌法研究了燃气涡轮压缩机在不确定工作条件下的响应。Liu 等［23］对涡轮叶片在风速不确定下的总体性能进行了讨论。di Stefano 等［24］研究了湍流模型闭合系数不确定性对超燃冲压发动机流场解的影响。Guo 等［25］通过任意多项式混沌的稀疏近似来评估制造可变性对压缩机叶片气动性能的影响。Huang等［26］提出了一种结合非嵌入式多项式混沌法和Smolyak 稀疏网格的不确定性量化方法，对转子叶尖的气动和传热性能不确定性进行量化。

国内方面，王晓东等采用嵌入式多项式混沌方法分别研究了Burgers 方程的随机响应［27］和随机方腔流动中不确定性因素的影响［28］。邬晓敬等［29］采用非嵌入式多项式混沌法对翼型跨声速随机气动特性进行不确定性及全局敏感性分析。另外，对多项式混沌法的改进也在持续进行。Zhao等［30］提出了一种高效且新颖的自适应多保真稀疏多项式混沌耦合Kriging 方法，该方法具有灵活性高，非线性建模能力强的优点。在Schaefer的最新研究［31］中提出了一种空间精确多项式混沌的新统计方法，该方法可以在整个飞行包线或设计空间内插补或外推偶然和认知不确定性。尽管已经有大量学者利用多项式混沌法开展不确定性分析研究，但不确定性分析中所需的计算成本仍然较高，尤其是当不确定性变量维度和多项式阶数增大时。

除了以上所述对不确定性进行分析和量化的研究，降低气动特性对不确定性变量的敏感性也是气动优化设计领域的一大挑战，这需要开展基于不确定性下的鲁棒优化设计。

大量研究工作已经基于多项式混沌法展开。根据鲁棒优化设计中是否使用梯度，可分为 PCE非梯度类鲁棒优化设计、PCE 梯度类鲁棒优化设计。基于非梯度类优化方法，Zein［32］结合多项式混沌法提出了一种信任区域优化方法，在信任区域上建立代理模型以完成鲁棒优化设计。Wang等［33］耦合了非嵌入式多项式混沌法与多目标遗传算法，并将其应用于压缩机转子叶片的鲁棒优化设计中。Palar 等［34］将进化算法和非嵌入式多项式混沌法结合，开展了跨声速翼型的鲁棒优化设计，目标为降低不确定性并最大化升阻比。国内方面，邬晓敬［35］耦合非嵌入式多项式混沌法和Kriging 代理模型发展了自适应鲁棒优化设计方法，对二维翼型进行了考虑不确定性的优化设计。

使用梯度优化算法仍然是解决大规模设计变量气动优化设计问题最有效的途径之一，对于考虑不确定性的优化设计其收益将更为明显。Padulo 等［36］提出了一种简化正交技术，可在不显著增加计算成本的条件下用于考虑较少设计变量的翼型气动优化设计中。Shankaran 等［37］提出了一个鲁棒优化框架，结合多项式混沌法和伴随理论来有效地获得梯度，以实现考虑马赫数不确定性的鲁棒优化设计。Schillings 等［38］基于多项式混沌和梯度算法对二维欧拉流动不确定性下的气动外形开展鲁棒优化设计研究，目标函数定义为均值和方差的组合。Rallabhandi 等［39］使用PCE方法将伴随导出的梯度与不确定度量化相耦合来同时对音爆进行鲁棒优化，同时降低音爆响度的均值和标准差。Boopathy 等［40］提出了一种半嵌入式随机Galerkin 方法，该方法可以将确定性导数用于伴随方法，从而产生随机的Galerkin 伴随解。Sabater 等［41］通过耦合非嵌入式高斯过程模型和伴随方程法搭建了鲁棒优化设计框架，为了适应更多的不确定性输入使用了梯度增强型的Kriging 模型，并成功应用于考虑了马赫数和迎角不确定性的跨声速二维翼型的优化设计，所提出的方法可以同时减少阻力的平均值和标准差。

结合以上总结和讨论，目前基于多项式混沌法的不确定性分析和梯度优化设计相关研究存在的不足为不确定性分析过程中计算成本较高，优化设计并未包含多种设计状态或输入不确定性，且对优化结果的分析不足。因此，本文的研究内容为首先利用伴随方程法求解目标函数对不确定性变量的导数，发展一种梯度增强型多项式混沌法，以降低优化设计中不确定性分析模块的计算成本，采用亚声速和跨声速二维翼型算例对该方法进行验证，并量化不确定性变量的全局敏感性。其次，建立不确定性分析模块统计矩梯度求解方法并搭建优化设计系统。最后，对低亚声速和跨声速二维翼型进行考虑马赫数和迎角不确定性的梯度优化设计，并对优化结果进行分析讨论。

1 数值模拟方法和伴随理论

1.1 数值模拟方法

采用有限体积法求解三维可压缩雷诺平均Navier-Stokes（RANS）方程，其积分形式如式（1）所示。湍流模型使用Spalart-Allmaras（SA）方程模型。

式中：V为控制体的体积边界；Q为流场守恒变量；FI和FV分别是无黏通量和有黏通量，在直角坐标系下可分解为3 个方向的分量。

空间离散采用基于有限体积法的JST 空间离散方法。时间推进上采用广义最小残差（Generalized Minimal Residual，GMRES）方法，该方法作为一种Newton-Krylov 子空间方法的分支，是目前较为先进的线性系统迭代求解方法之一。

1.2 求解器验证

验证模型为ONERA-M6 机翼。计算状态为Ma=0.84，Re=11.72×106，α=3.06°，该状态具有较为完备的试验数据［42］。利用商业软件ICEM 划分多块结构O-H 型网格，网格量为158 万，边界层第1 层高度为1×10-6。物面和对称面网格如图1 所示。

图1 M6 机翼网格Fig.1 M6 wing mesh

沿机翼展向分别截取20%展长、44%半展长和65%半展长3 个剖面，将求解器的计算结果和实验数据进行对比，如图2 所示。图中，圆形、方形和菱形数据点为实验数据（Exp），实线为计算得到的截面压力分布，可以看出计算结果和实验数据在各个机翼展向截面吻合均较好，说明采用的CFD 求解器满足优化设计的精度要求。

图2 M6 机翼计算结果与实验数据对比Fig.2 Comparison of M6 wing calculation results with experimental data

1.3 伴随方程

在梯度优化设计中，高效精确地获得目标函数对设计变量的导数成为关键一环。伴随方程法求解梯度的效率几乎不受设计变量个数的影响，对于具有高维特性的气动优化设计问题具有显著优势。

给定目标函数J和设计变量X。计算网格是设计变量的函数G(X)。对于RANS 方程，流场解是计算网格和设计变量的函数Q(G(X)，X)。

目标函数通过对收敛的流场解Q进行积分得到，有

对于收敛的流场解残差R为0，即

当给定流场解Q时，根据链式求导法则得到目标函数对设计变量的Jacobian矩阵：

为了避免求解计算最为耗时的dQ/dX一项，引入伴随方程：

式中：ψ为伴随向量。可表示为

从伴随方程的组成上看，求解伴随方程并不依赖于设计变量。尽管气动优化问题具有明显的高维特性，然而求解伴随方程需要的时间与单次CFD计算所需的时间大体相当，大大提升了计算目标函数对设计变量梯度的效率。通过求解伴随方程，可以得到伴随向量，将式（6）代入式（4）中得到：

式中：∂J/∂G的计算使用收敛的流场解，对网格变量求一次偏导数即可；dG/dX可根据参数化方法和网格变形算法计算得到。

1.4 梯度验证

使用有限差分法对伴随方程求解所得梯度进行验证。为保证梯度验证的普适性，随机挑选某翼型进行梯度验证，如图3 所示，在翼型四周布置FFD 控制框。FFD 控制框弦向共12 个控制点，控制点移动方向为y向。在翼型前后缘施加FFD 控制点的移动约束，上下表面FFD 控制点在y方向的移动大小相等，方向相反，以保证前后缘位置不变。由此总的设计变量个数为10×2+2（翼型前后缘设计变量）=22。

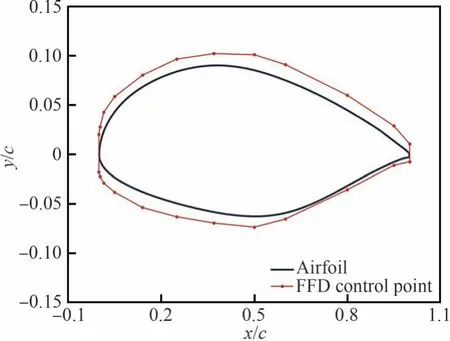
图3 梯度验证翼型几何和FFD 控制框Fig.3 Airfoil geometry and FFD control frame for gradient validation

该翼型计算状态为Ma=0.69，α=-0.39°，Re=11.7×106，对应于Honda 飞机巡航状态［43］。表1 和表2 分别展示了针对目标函数CL和CD利用有限差分方法和耦合伴随方程计算得到的导数值。从对比结果上看，伴随方程法求解得到的梯度与有限差分法吻合较好，相对误差在10-3以下，符合有限差分截断误差精度。

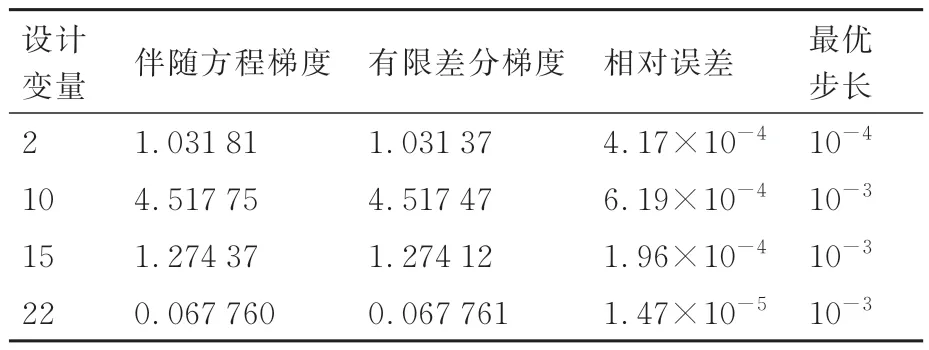
表1 升力系数关于设计变量的梯度验证Table 1 Gradient verification of lift coefficients with respect to design variables

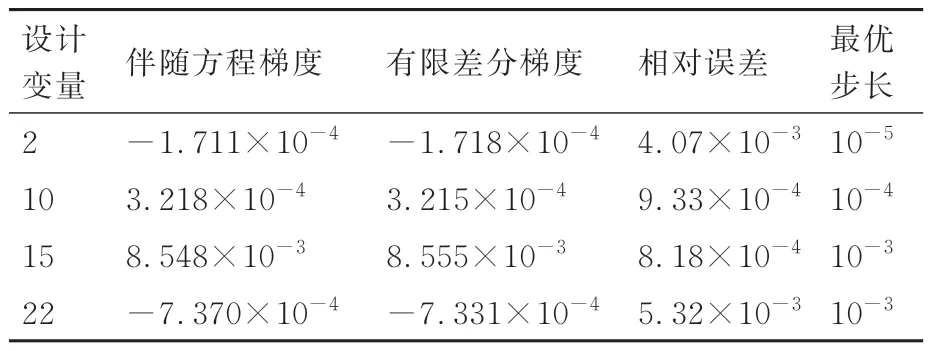
表2 阻力系数关于设计变量的梯度验证Table 2 Gradient verification of drag coefficients with respect to design variables

2 不确定性分析方法

2.1 多项式混沌法原理

考虑一个可由确定性映射表示的物理模型系统Q=M(X)，这里X=[X1，X2，…，XN]T，N≥1 是输入变量向量（包括几何设计变量和来流条件变量等）。Q=[Q1，Q2，…，QM]T，M≥1 是系统提供的一组输出变量向量。

由于假设输入向量X中部分n个变量受不确定性影响，因此这一部分的变量可由具有指定概率密度函数（Probability Density Function， PDF）的随机向量x表示。另一部分的输入变量为确定性变量，用D表示。这里x为真实随机变量，其可看作标准随机变量ξ的函数：

式中：μ和σ分别是该随机变量的均值和方差。通过不确定性传播，导致该系统的输出响应Q也是随机变量。

多项式混沌法（Polynomial Chaos Expansion， PCE）的核心思想是通过含有独立随机变量的正交多项式基寻找随机变量ξ（输入参数）与感兴趣量Q（QoI）之间的函数依赖关系。将随机函数Q分解成确定和随机两部分，得到式（9）所示的无穷级数表达形式：

在实际使用中，取前P阶有限模态截断，如式（10）所示。在气动优化设计中D为确定性设计变量向量，ξ为随机设计变量向量（如迎角、马赫数、来流湍流度等）。那么αj(D)为该多项式混沌展开第j阶的确定性部分，而Ψj(ξ)则为该多项式混沌展开第j阶的随机部分。

采样总数Ns为P+1，由3 个参数确定：随机变量的数量p，独立基函数多项式的阶数p和过采样率np，如式（11）所示。

经过文献中的研究，过采样率一般为2，即可在满足多项式混沌法精度的情况下，最大限度地减少采样点的个数。

多项式混沌法的关键在于求解正交多项式的权重系数αj(D)，采用点配置回归法进行求解。回归方法即采用最小二乘方法求解通过确定性抽样构建的线性方程组。

在随机空间中选择Ns个样本，并在这些点评估确定性问题。最后，针对随机变量的频谱模式，建立了一个由Ns个方程组成的线性系统并求解。该线性系统由式（12）给出：

式中：矩阵中的ξ0代表该标准随机变量矢量ξ在第一个采样点处的值，同理ξNs-1为标准随机变量矢量ξ在第Ns个采样点处的值。最终待求系数矩阵写成紧致格式为

多项式混沌法的最大优点是可解析表达输出随机变量的均值和方差。根据对均值（数学期望）和方差的统计定义，由多项式混沌法得到的输出随机变量的均值和方差可表示为式（14）和式（15）：

2.2 梯度增强型多项式混沌法

多项式混沌法的精度和基函数的阶数有关，为提高精度需要增加基函数的阶数。由式（11）可知阶数的增加会导致采样点数的成倍增加，即需要调用成倍数量的CFD 数值模拟，需要大量的计算资源。

考虑到多项式混沌法精度和采样点数的矛盾，采用伴随方程法获取梯度信息，进而对多项式混沌法进行增强。梯度增强型多项式混沌法（Gradient-enhanced Polynomial Chaos Expansion， GPCE）可以在保证不增加基函数阶数的情况下显著提高多项式混沌法的精度。简而言之，梯度增强型多项式混沌法可在保证相同的模拟精度下，大幅减少采样点的个数。

使用这种梯度增强型多项式混沌法，可以构建基于二阶回归的全局敏感性分析，其成本仅随着维度的增加而线性增加。因此，这种方法甚至可以应用于大维数问题。

梯度增强型多项式混沌法可通过对式（10）所示的PCE 核心公式微分得到。等式的左右两边同时对归一化的标准随机变量求导数可以得到：

式（16）展开写成矩阵形式，如式（17）所示：

对于Ns个样本ξ0，ξ1，…，ξNs-1，n个标准随机变量ξi，ξi+1，…，ξn，n个真实随机变量xi，xi+1，…，xn，左端项P+1 个多元联合基函数Ψj分别对n个归一化标准随机变量ξi求导数∂Ψj/∂ξi。

式（17）右端项中∂Q/∂x为在每个确定性采样点处感兴趣的输出变量Q对n个真实随机输入变量的确定性梯度，其可以由伴随方程法直接得到。

由于真实随机变量x又是标准随机变量ξ的函数，那么∂xj/∂ξj可以基于不确定性变量的已知分布获得。例如，一个均值为μ和标准差为σ的正态分布，单位化形式为

该导数为

如图4 所示，通过在式（10）左右两端增加梯度信息对线性系统进行增广处理。最终得到的基函数梯度增广矩阵（17）大小为Ns(n+1)×Nb，右端项输出矩阵大小为Ns(n+1)×Nq，PCE 待求系数矩阵的大小不变，仍然为Nb×Nq。采用梯度增强型PCE，需要的采样点数仍为Ns，相比于同等精度的PCE 可减少nNs个采样点。换言之，利用Ns个样本点可构建与Ns(n+1)个样本点具有相同精度的多项式混沌响应面。

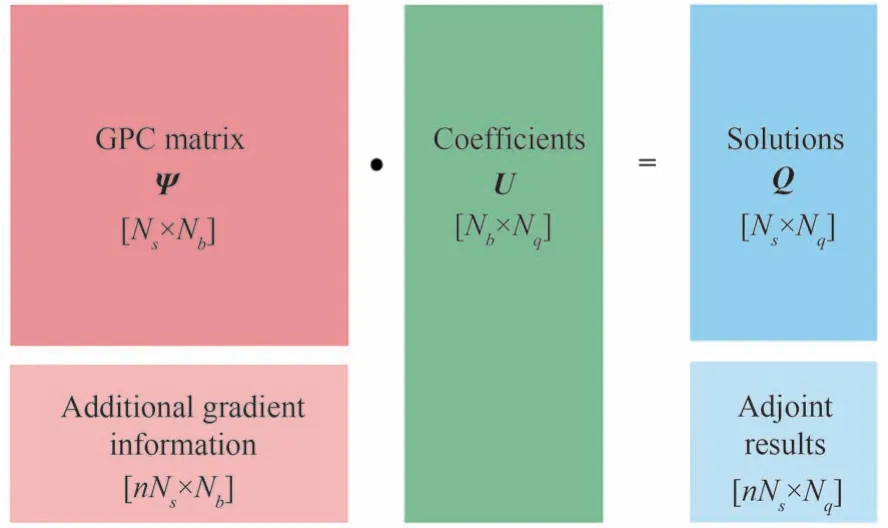
图4 梯度增强型多项式混沌法Fig.4 Gradient-enhanced polynomial chaos expansion method

2.3 基于方差分解的全局敏感性分析方法

通过不确定性分析，可以得到不确定性因素对输出的影响，但是要确认每一个不确定性变量对这一影响的贡献程度，还需要进行敏感性分析。敏感性分析分为全局敏感性分析和局部敏感性分析。全局敏感性分析可以克服局部敏感性分析的局限性，不仅考虑了各因素概率密度函数的分布和形态的影响，而且在分析时所有因素可同时变化，还可以不受模型限制并考察输入参数在整个参数变化范围内对输出的贡献程度。本文采用基于方差分解的全局敏感性分析方法。

由方差降维分析，总方差可以表示为

式中：

方差分解显示了如何将模型输出的方差分解为可归因于每个输入的项，以及它们之间的交互作用。所有项加在一起就是模型输出的总方差。根据以上的数学推导，定义一种基于直接方差分解的敏感性度量Sobol 指数，如式（22）所示。

式中：Si称为“一阶敏感性指标”或“主效应指标”，其反映的是Xi对输出方差的贡献，由总方差进行归一化。同理，可以通过将方差分解中的其他项除以Var(Q) 来形成高阶交互的Sobol 指数Sij，Sijk等：

基于多项式混沌法的Sobol 指数可以方便地表示为式（24）和式（25），详细推导见文献［44］。

2.4 统计矩梯度求解

基于梯度的不确定性优化设计需要求解不确定性分析模块的梯度信息，即包括随机输出变量均值对设计变量的梯度dμQ/dD和标准差对设计变量的梯度dσQ/dD。

由PCE 方法可知，随机输出变量Q的均值和方差可以解析地表达为式（14）和式（15）。将均值对设计变量进行微分，得到式（26）。

式中：dQ/dD是每个确定性采样点处输出变量Q对设计变量的梯度，该项由伴随方程法直接获得。那么该式可以简单地理解为输出变量均值对设计变量的梯度等于输出变量对设计变量梯度的均值。

输出变量方差对设计变量的梯度可以表示为

为了求式（27）的梯度值，需要确定多项式系数对设计变量的梯度dαj/dD。对于第个设计变量，可以通过对PCE 核心公式微分来构造第二个多项式混沌展开。式（10）的多项式混沌法核心公式左右两端同时对设计变量求导可得

式中：左端项∂Y(D，ξ)/∂Dj可由伴随方法求得；右端项中Ψi(ξ)为在构建PCE 时选定的多项式基函数，那么待求项只剩这个新构造的多项式展开的新系数dαi(D)/dDj，同样可利用回归方法求解。

对于nDV个设计变量，需要构建nDV个线性系统，如式（29）所示：

通过求解这nDV个线性系统，可得到输出变量Q对nDV个设计变量的导数dQ/dD。

3 优化设计框架

3.1 优化设计辅助技术

采用FFD 参数化方法。FFD 参数化方法基于弹性体变形思想来表示几何变形问题。其核心公式为

式中：Xs为设计外形上任意一点的全局坐标向量，(u，v，w)为其参数坐标向量，u，v，w的取值范围为(0，1)；Pi，j，k是控制框中每个控制点的全局坐标向量。

选择逆距离权重插值算法（Inverse Distance Weighting， IDW）作为本文的网格变形算法，以建立网格变形方法的实质是建立空间网格与表面网格的映射关系。IDW 算法的核心公式为

式中：N是选为插值基点的个数；u(xv)为空间网格待插值点；uj为表面网格插值基点；wj为第j个位置的权重系数，与空间网格插值点到表面网格插值基点的距离成反比。

经大量实践发现，序列二次规划算法是目前针对高维度大规模设计变量光滑非线性规划问题表现最优的算法之一。本文使用基于序列二次规划算法的SNOPT 作为优化算法。

3.2 确定性优化设计框架

结合3.1 节介绍的优化设计辅助技术，可最终搭建如图5 所示的确定性优化设计系统。具体优化步骤如下：

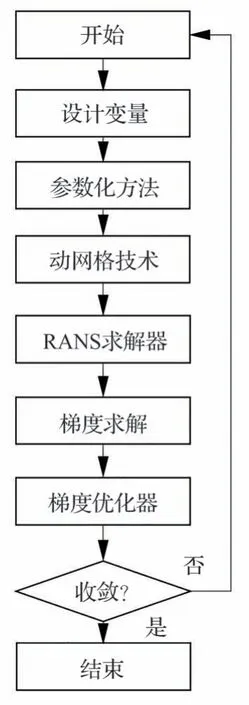
图5 确定性优化设计框架Fig.5 Deterministic optimization design frame

1）建立初始模型和网格，给定设计变量的初值X0。

2）通过FFD 方法对表面网格xs进行参数化变形。

3）基于第2）步变形后的表面网格，通过IDW 动网格技术得到变形后的空间网格xv。

4）求解器求解RANS 方程，计算流场结果Q。

5）基于流场结果，计算伴随方程并求解目标函数对设计变量的梯度信息dJ/dX。

6）结合第4）步中流场计算结果和第5）步中的梯度信息，使用SNOPT 优化算法对设计变量进行更新。

7）重复第2）步～第6）步，直至优化设计收敛。

3.3 不确定性优化设计框架

考虑不确定性后，修改目标函数为输出变量的 均 值 和 方 差 的 线 性 组 合J=K1×μq+K2×σq，优化设计系统中需引入多项式混沌法分析模块来计算不确定性的传播过程，并得到输出变量的均值和方差及两者对设计变量的梯度信息。最终可搭建如图6 所示的不确定性优化设计系统。具体优化步骤如下：

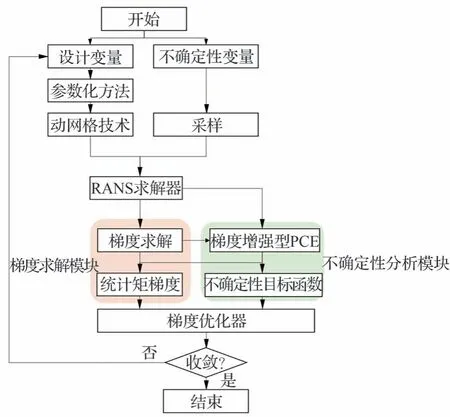
图6 不确定性优化设计框架Fig.6 Uncertain optimization design frame

1）建立初始模型和网格，给定设计变量的初值X0。

2）通过FFD 方法对表面网格xs进行参数化变形。

3）基于第2）步变形后的表面网格，通过IDW 动网格技术得到变形后的空间网格xv。

4）设定不确定性变量，例如马赫数M或迎角α等。根据不确定性变量在随机空间进行采样，采样数为Ns。

5）求解器在每个采样点进行确定性分析，求解RANS 方程，计算流场结果Q。

6）基于流场结果，在每个采样点进行确定性分析计算伴随方程，得到不确定性输出变量q对设计变量的导数dq/dX。

7）基于确定性分析结果，构建梯度增强型多项式混沌线性方程组ΨC=Q，求解系数矩阵C，得到输出变量的均值μq和方差σq。

8）利用确定性分析所得梯度耦合多项式混沌系统的梯度，求解输出变量均值及方差对设计变量的导数dμq/dX，dσq/dX。那么目标函数的梯度可由两者进行线性表示：

9）根据第8）步中的梯度信息，使用SNOPT优化算法对设计变量进行更新。

10）重复第2）步～第9）步，直至优化设计收敛。

4 考虑飞行条件不确定性的翼型不确定性分析

本节将以亚声速及跨声速翼型算例进行不确定性分析，同时可验证梯度增强型多项式混沌法的计算精度。

4.1 亚声速翼型

选择NACA0012 翼型进行亚声速状态全湍流下多项式混沌法不确定性分析的精度测试。假设马赫数满足Ma～N(0.5，(0.02)2)的正态分布，迎角满足α～N(1.5，(0.2)2)的正态分布。

计算高度为10 km，计算网格如图7 所示，采用全湍流计算。为验证多项式混沌法的精度，分别进行5 000、10 000 次蒙特卡洛法作为验证标准。蒙特卡洛法在采样点总数足够多时，其所得结果趋近于真实值。计算结果如表3 所示。2 次采样的结果在均值上基本一致，方差上有较小的不同，数值上基本收敛，因此可作为验证多项式混沌法的标准。

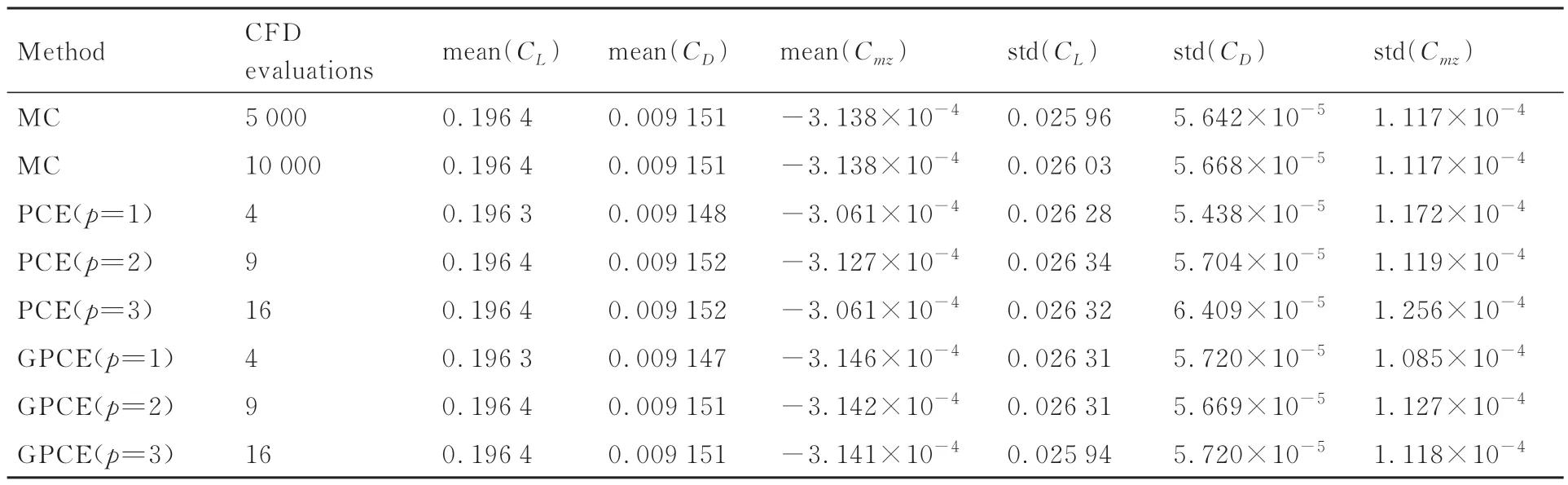
表3 亚声速翼型：蒙特卡洛法和PCE 法计算结果Table 3 Subsonic airfoil： Monte Carlo and PCE calculation results

图7 NACA0012 网格Fig.7 NACA0012 mesh

为检验PCE 方法的精度，定义PCE 方法的相对误差为

式中：J=mean(CL)，mean(CD)，mean(Cmz)，std(CL)，std(CD)，std(Cmz)。

使用1～4 阶的独立基函数多项式，采样点数从10～70 个不等，分别采用传统PCE 方法和梯度增强型PCE 方法得到误差在阶数和采样点数空间内的分布，如图8 所示。图中显示的是3 个力系数均值和方差的相对误差总和，即

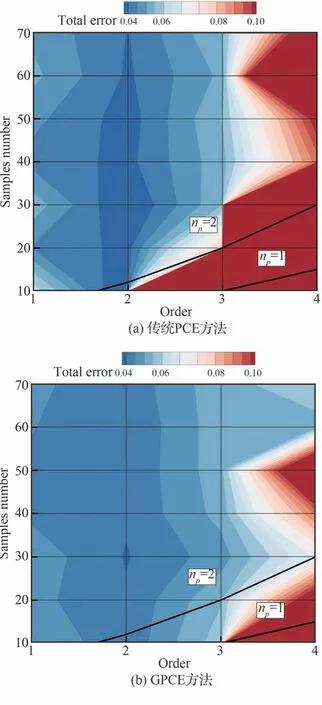
图8 亚声速翼型：传统PCE 和梯度增强型PCE 的精度对比Fig.8 Subsonic airfoils： Accuracy comparison of conventional PCE and gradient-enhanced PCE

从表3 中可以看出和蒙特卡洛法的结果对比，GPCE 方法在预测力系数标准差的精度上具有明显优势。同时，梯度信息的引入对低阶多项式混沌法的精度增强效果较弱，但能在一定程度上减轻高阶多项式混沌法的过拟合现象，从而提高精度。这一点从图8 中也能看出，梯度增强型的PCE 方法大幅增加了采用3 阶或4 阶基函数时多项式混沌法的拟合精度。对于亚声速全湍流状态，采用1 阶或2 阶的多项式混沌法已经可以满足预测精度的要求，更高阶的基函数不仅会增加采样点的个数和计算成本，还会导致精度降低。

分别使用蒙特卡洛法和梯度增强型PCE 法计算得到的亚声速翼型表面平均压力分布系数沿弦向的分布如图9 所示。图中实线表示在不确定输入的影响下压力系数的均值，阴影部分表示压力系数均值上下正负3 倍标准差区间。从图中可以看出，受输入不确定性影响最大的是翼型头部，梯度增强型PCE 法模拟的均值和标准差与蒙特卡洛法几乎完全重合，具有较高的精度。

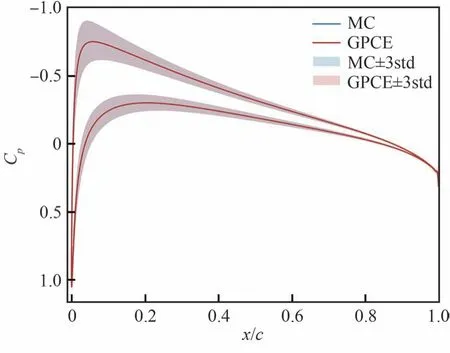
图9 亚声速：表面压力系数不确定性响应对比Fig.9 Subsonic： Comparison of surface pressure coefficient uncertainty response

图10 和图11 分别展示了蒙特卡洛法和梯度增强型多项式混沌法计算得到的流场平均压力系数分布和压力系数在流场中的标准差云图。从标准差云图上看，NACA0012 翼型在给定的马赫数和迎角输入不确定性条件下，空间流场的不确定性主要集中在翼型的前50%弦长，尤其是上表面的负压峰处，受不确定性影响最为显著。对比蒙特卡洛法得到的流场结果和多项式混沌法得到的流场结果，两者高度相似。

图10 亚声速翼型：2 种方法流场压力系数均值对比Fig.10 Subsonic airfoils： comparison of mean values of flow field pressure coefficients between two methods Subsonic airfoils

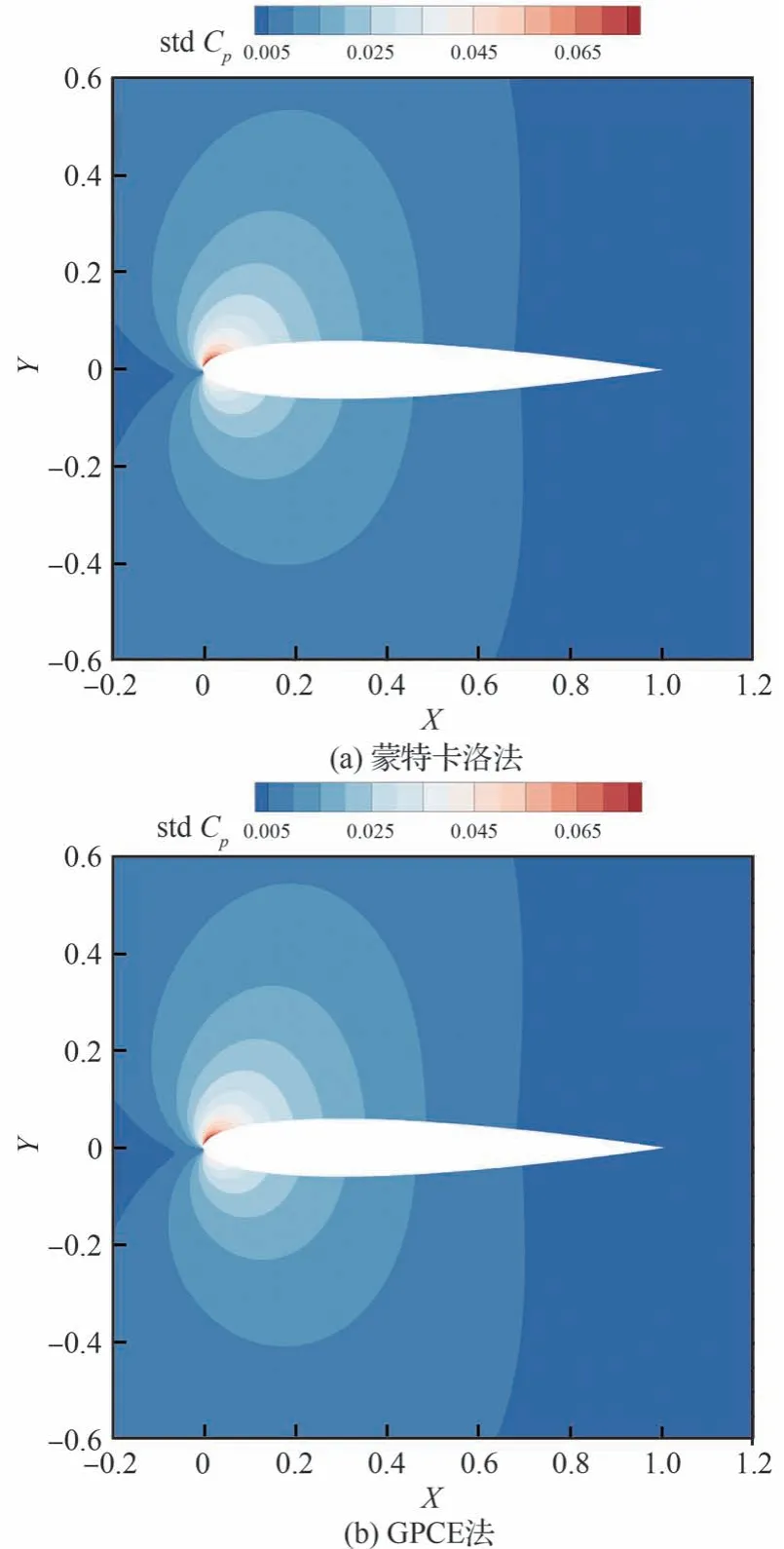
图11 亚声速翼型：2 种方法流场压力系数标准差对比Fig.11 Subsonic airfoils： Comparison of standard deviation of flow field pressure coefficient between two methods

图12 所示为翼型表面归一化Sobol 指数沿弦向的分布。图中［-1，0］为下表面，［0，1］为上表面。Sobol指数在上下表面近似呈对称分布，在上下表面前90%弦长范围内都由迎角的不确定性主导，而在前后缘的10%范围内受马赫数不确定性影响较大。2个不确定性参数之间基本不存在耦合效应。

图12 亚声速表面 Sobol 指数弦向变化Fig.12 Subsonic surface Sobol exponent chordwise variation

受马赫数和迎角2 种不确定性影响的翼型空间流场归一化Sobol 指数云图如图13 和图14 所示。图中显示出在亚声速全湍流状态下，马赫数不确定性主要影响翼型头部和尾部的流场方差，而其他空间流域内的不确定性主要由迎角的不确定性支配。两种不确定性因素之间的耦合作用较小。

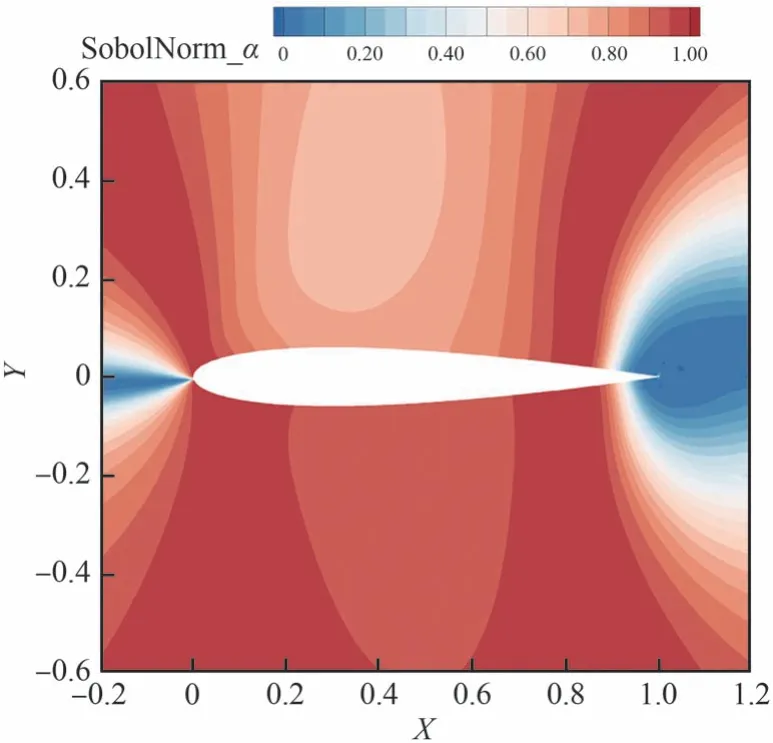
图13 亚声速Sobol 指数：迎角Fig.13 Subsonic sobol index： Angle of attack

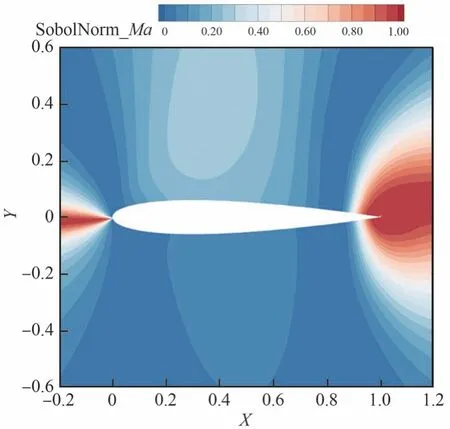
图14 亚声速Sobol 指数：马赫数Fig.14 Subsonic sobol index： Mach number

4.2 跨声速翼型

选择RAE2822 翼型进行跨声速状态全湍流下多项式混沌法不确定性的精度测试，并对该状态进行不确定性分析和全局敏感性分析。

计算网格如图15 所示，弦向布置281 个网格点，法向121 个网格点，附面层第1 层高度1×10-6。计算状态为Re= 6.5×106，马赫数满足Ma～N(0.734，(0.02)2)的正态分布，迎角满足α～N(2.79，(0.2)2)。选取的状态流场中具有强激波，呈现高度非线性效应，对验证工作有益［45］。分别进行了5 000、10 000 次蒙特卡洛分析，得到力系数的计算结果如表4 所示。表中显示5 000、10 000 次蒙特卡洛法的结果，2 次结果较为接近，可认为蒙特卡洛法收敛，将其作为检验多项式混沌法精度的标准。

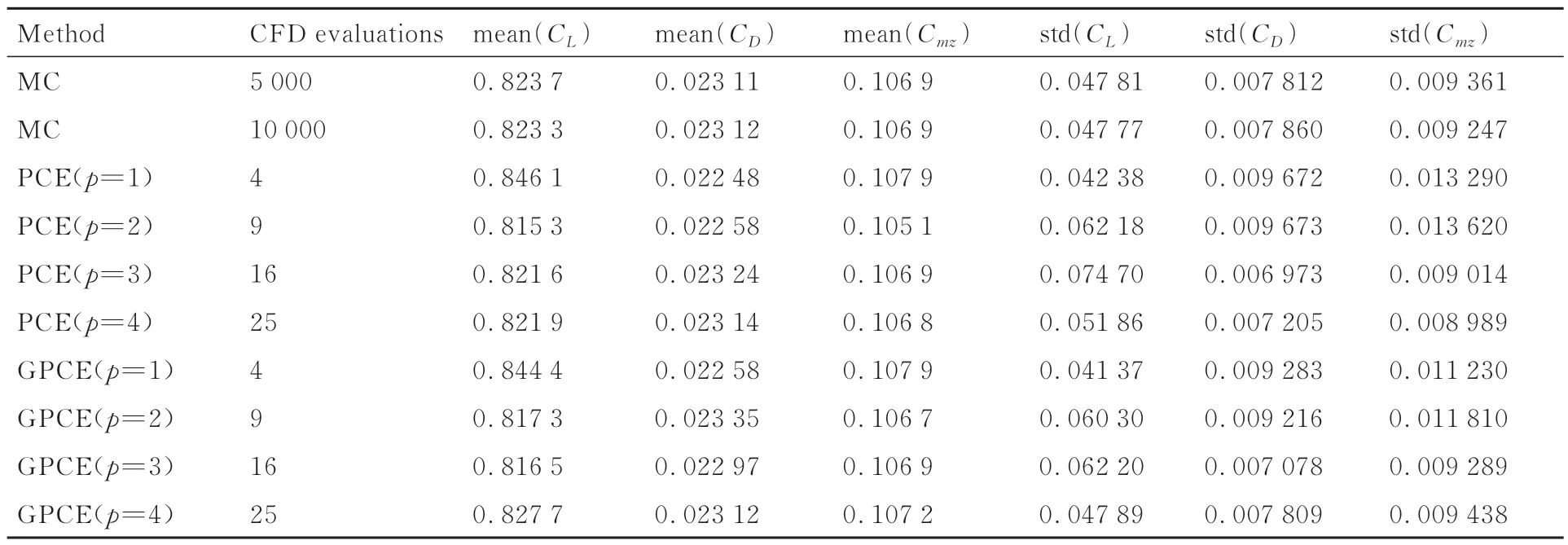
表4 跨声速翼型：蒙特卡洛法和PCE 法计算结果Table 4 Transonic airfoils： Monte Carlo and PCE calculation results

图15 RAE2822 翼型计算网格Fig.15 RAE2822 airfoil mesh

分别使用1～4 阶传统PCE 方法和梯度增强型PCE 方法进行该问题的不确定性传播，结果如表4 所示。在跨声速条件下，流场非线性效应大幅增加，从而增加了PCE 方法的预测难度。从表中可以看出，传统PCE 方法和蒙特卡洛法在各个力系数均值的结果上差异较小，而在力系数标准差的预测上两者误差有所增大。梯度增强型PCE 方法的模拟精度较传统PCE 方法具有一定提升，其主要体现在对力系数标准差的预测上，例如对比PCE（p=4）和GPCE（p=4）。

同样，利用亚声速下的精度验证方法，即式（33），选取采样点数从6～50 个不等，分别采用传统PCE 方法和GPCE 方法得到误差在阶数和采样点数空间内的分布，如图16 所示。图中显示，在跨声速状态下GPCE 方法仍能在一定程度上减轻高阶多项式混沌法的过拟合现象，例如4阶和5 阶。尽管GPCE 方法相比于传统PCE 方法的优势在跨声速状态下整体上有所减弱，然而需要注意到其重点改善了低阶、小样本数情况下的拟合精度，这对于减少计算成本是有利的。

图16 跨声速翼型：传统PCE 和梯度增强型PCE 的精度对比Fig.16 Transonic airfoils： Accuracy comparison of conventional PCE and gradient-enhanced PCE

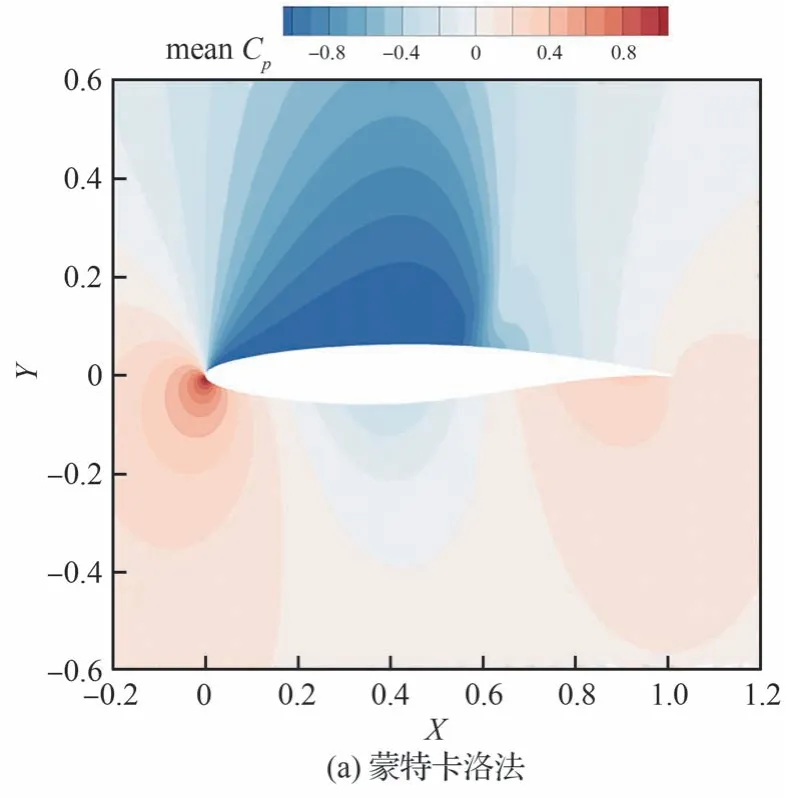
使用蒙特卡洛法和GPCE 法计算得到的流场中压力系数均值和标准差云图如图17 和图18所示。对比2 种方法的结果可以看到，GPCE 法能够较为精确地模拟不确定性在跨声速流场中的传播，包括流场中具有较强非线性的激波区域。从压力分布均值上看，在该状态下翼型上表面 60%弦长处存在一道强激波。相应的，标准差云图中显示出该位置受不确定性影响最明显，标准差最大。

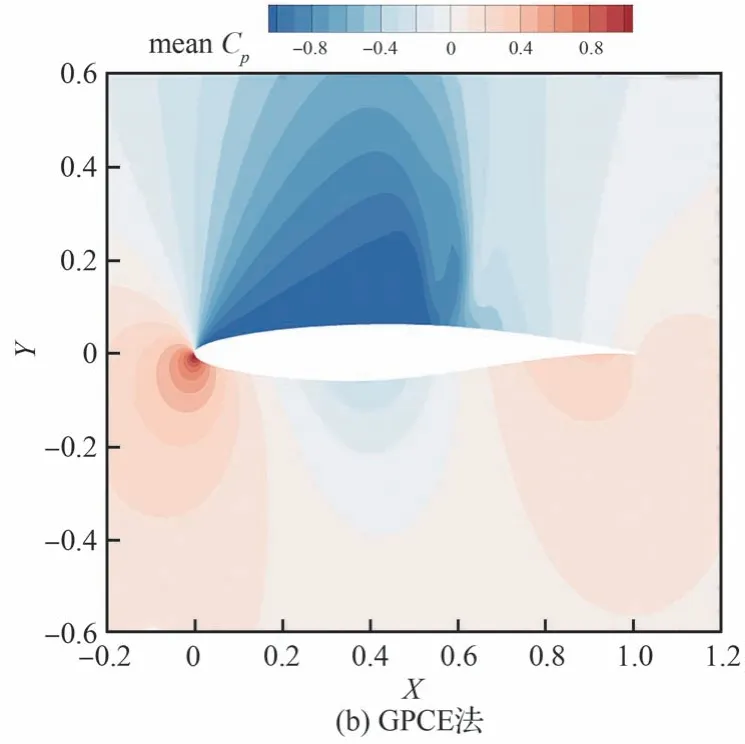
图17 跨声速翼型：2 种方法压力系数均值对比Fig.17 Transonic airfoils： Comparison of mean values of flow field pressure coefficients between two methods

图19 所示为翼型表面 Sobol 指数沿弦向的分布，在跨声速状态下，占主导地位的是马赫数，在激波位置附近马赫数、迎角及其耦合作用存在竞争。

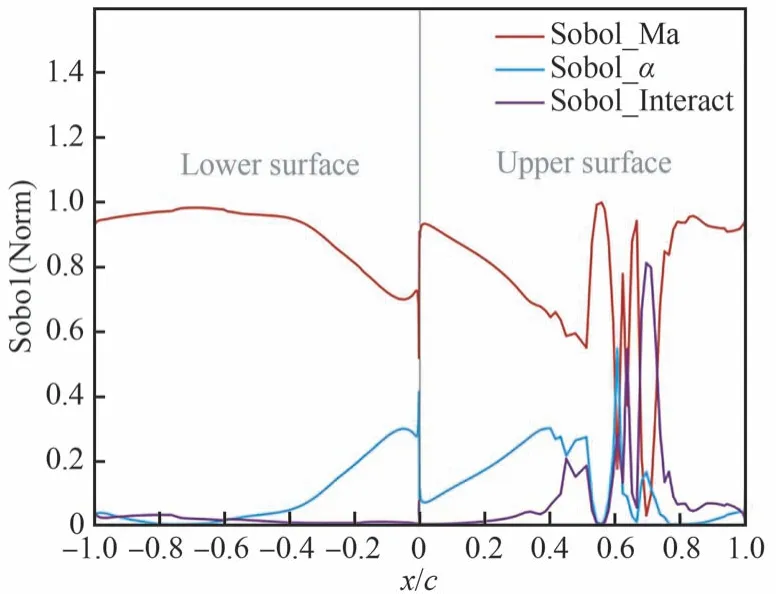
图19 跨声速表面 Sobol 指数弦向变化Fig.19 Transonic surface Sobol exponent chordwise variation

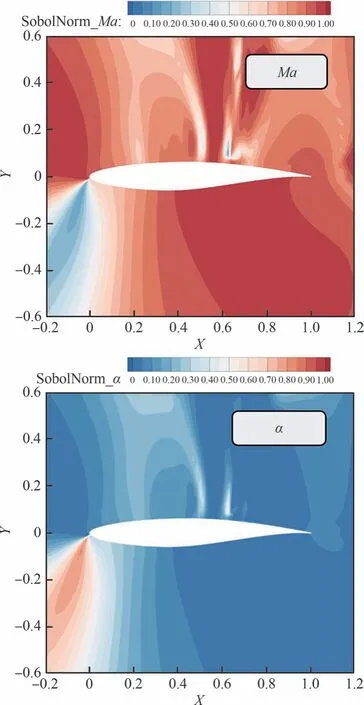
通过梯度增强型多项式混沌法求解的归一化Sobol 指数云图如图20 所示。从图中可以看出，在跨声速全湍流流场中，马赫数不确定性占主导地位，其影响流场中的大部分区域，尤其是激波位置处，但对下表面前缘区域影响较小，由于本例为正迎角工况，因此该处主要受迎角不确定性的影响。马赫数和迎角的交互作用主要集中在翼型上表面激波前后区域。

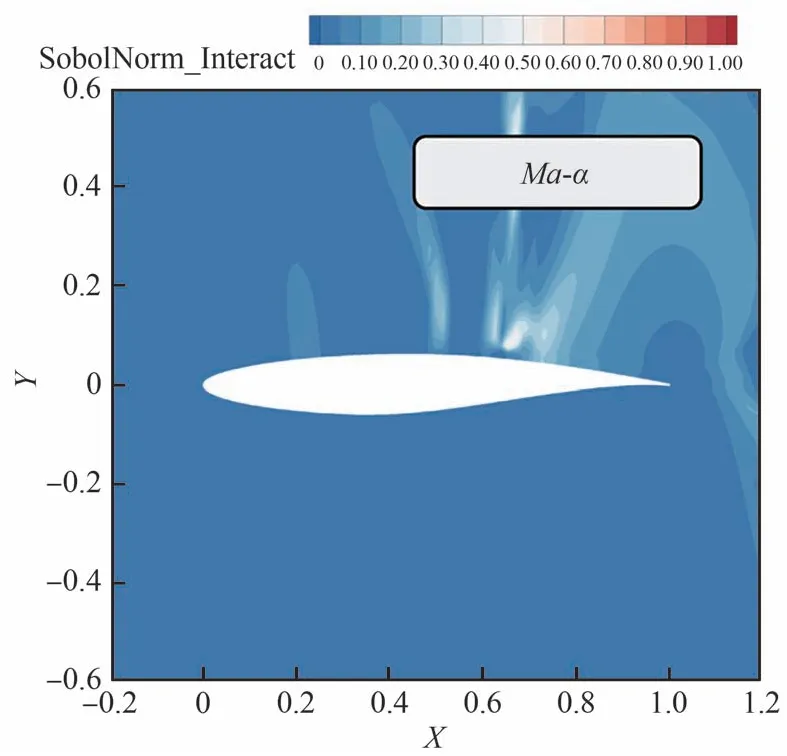
图20 跨声速全局敏感性分析结果Fig.20 Transonic global sensitivity analysis results

5 考虑飞行条件不确定性的翼型确定性及不确定性优化设计

5.1 低亚声速翼型优化设计

初始翼型选择RAE2822，参考Cessna 状态，Ma= 0.19，Re= 5×106，CL= 0.3。FFD 控制框如图21 所示。控制框在翼型头部加密以更好地控制翼型前缘的型面。定义式（35）所示的确定性和不确定性优化问题。

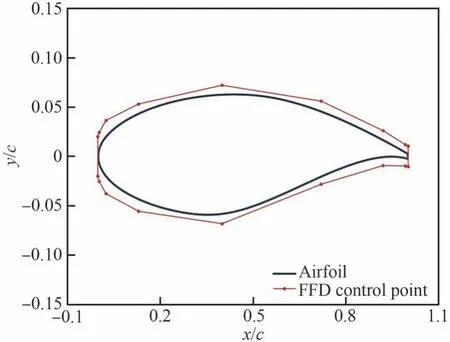
图21 翼型优化FFD 控制框Fig.21 Airfoil optimization FFD control frame

优化过程中设计变量总数为16 个，均为几何设计变量。不确定性优化中假设马赫数和迎角分别满足Ma～N(0.19，(0.05)2)的正态分布和α～N(0.45，(1.0)2)的正态分布，此时均值状态下翼型升力系数为0.3。优化过程中使用3 阶梯度增强型多项式混沌法，预测误差可保持在0.1%左右。

表5 给出了低亚声速翼型优化的确定性和不确定性力系数结果，其中各确定性的力系数为基准流场结果，即Ma=μ(Ma)，α=μ(α)。确定性优化设计结果命名为DeOpt （Deterministic Optimization）；不确定性优化设计结果命名为UMOpt （Uncertainty Multiple factor Optimization）。从表5 中的确定性力系数可以看到，确定性优化最终减阻10.03 counts，约为10.15%。其中主要减少的是压差阻力，而摩擦阻力几乎保持不变。不确定性优化总减阻量为9.33 counts，略小于确定性优化。另一方面，从阻力系数的不确定性统计响应结果上看，不确定性优化无论是均值还是标准差均要小于初始构型和确定性优化结果。相比于初始构型，不确定性优化结果阻力系数均值减少约17%，阻力系数标准差减少约80%。综合以上两个方面，可以得出结论：不确定性优化在确定性基准场的性能上有所牺牲，以换取在扰动范围内性能的鲁棒性。

表5 低亚声速翼型优化结果（阻力系数单位为counts）Table 5 Low subsonic airfoil optimization results （Drag coefficient in counts）

对比确定性和不确定性的结果，如图22 和图23 所示。UMOpt 翼型上表面前缘厚度较DeOpt 翼型有所增大，下表面前缘的前加载现象消失，厚度增大在压力分布上体现为上下表面的顺压梯度相比于DeOpt 翼型增大，吸力峰位置前移。

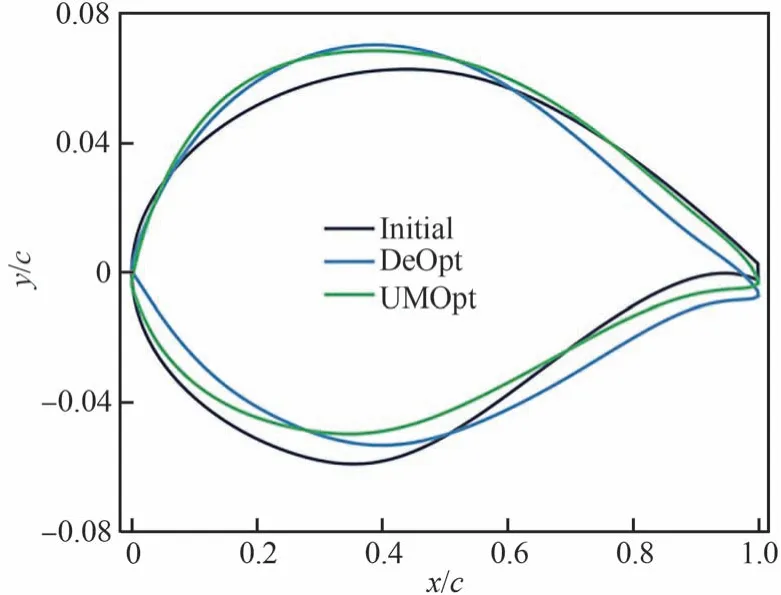
图22 低亚声速确定性及不确定性优化翼型对比Fig.22 Comparison of low subsonic deterministic and uncertain optimized airfoils

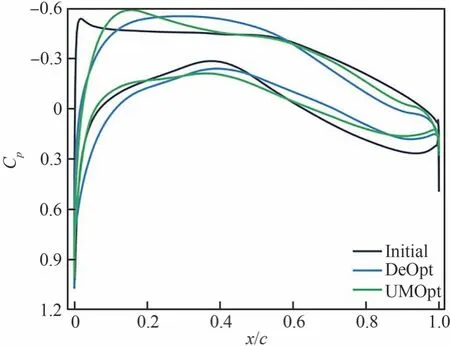
图23 低亚声速确定性及不确定性优化压力分布对比Fig.23 Comparison of low subsonic deterministic and uncertain optimal pressure distributions

采用蒙特卡洛法在随机空间内采样并进行确定性分析，得到的随机样本点阻力系数分布如图24 所示。小提琴图代表样本点阻力系数的分布特性，图中越饱满的部分其概率密度越大，样本点落在该区间的个数越多。每个小提琴图中心的黑色粗实线代表上下四分位数的区间，中间点代表整体数据的中位数。因此直观上看，小提琴图的上下位置可近似代表阻力系数平均值的高低，越靠下的代表平均阻力系数更低；小提琴图的形状代表了阻力性能的鲁棒性，越细长的小提琴图说明阻力系数标准差更大鲁棒性更差，越短粗的说明阻力系数标准差更小，性能更加集中，鲁棒性更好。对比3 种翼型的小提琴图结果发现，UMOpt 翼型具有明显优势。初始构型无论是平均性能还是性能的鲁棒性都较差，DeOpt翼型和UMOpt 翼型均大幅降低了阻力系数的平均值，但相比来讲UMOpt 的性能更加向平均值集中。

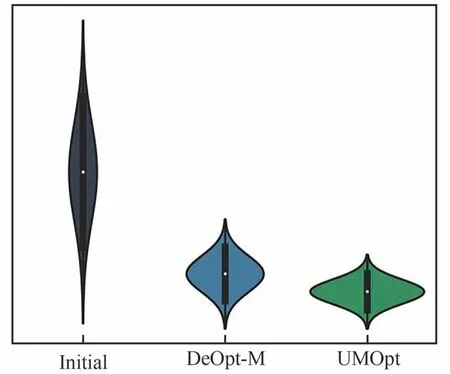
图24 低亚声速确定性及不确定性优化阻力系数的随机分布Fig.24 Random distribution of drag coefficients for low subsonic deterministic and uncertain optimization

将初始构型、DeOpt 翼型、UMOpt 翼型受马赫数和迎角不确定性影响的空间流场压力系数标准差云图进行对比。从图25 中可以看出在上表面前缘位置处流场压力系数标准差大小排序为UMOpt＜DeOpt＜Initial。因此，全湍流下考虑不确定性的优化设计相比于确定性优化设计更能有效降低空间流场内压力系数的不确定性，体现了不确定性优化设计的优势。

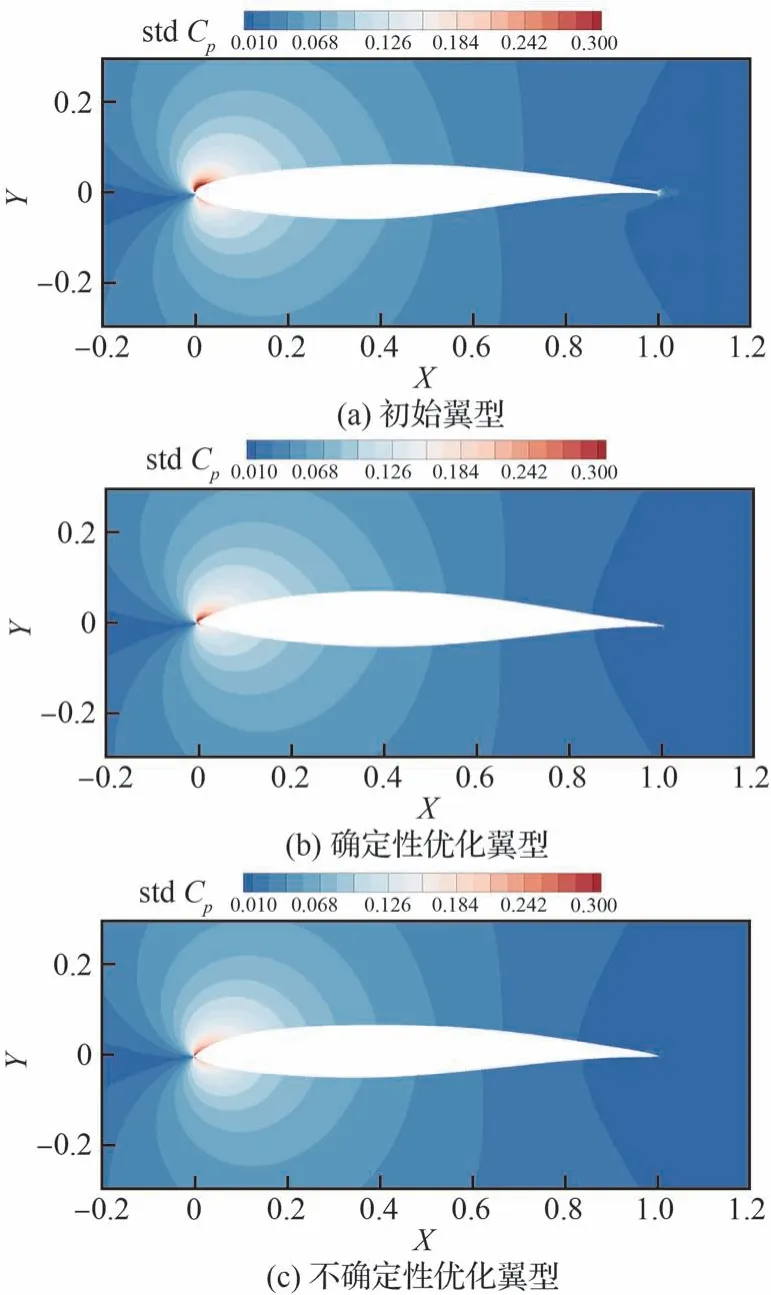
图25 考虑马赫数和迎角不确定性下初始、确定性及不确定性优化结果空间流场压力系数标准差云图Fig.25 Standard deviation contour of pressure coefficient of initial， deterministic and uncertain optimization results considering uncertainty of Mach number and angle of attack

确定性和不确定性优化历程如图26 所示。各个图中确定性优化历程以三角形在线中标示，不确定性优化历程以圆形在线中标示，不确定性优化过程中确定性基准场阻力系数以灰色线表示。由于不确定性优化中的目标函数为J=μ(CD)+σ(CD)，因此灰色圆形标注线和黑色圆形标准线之间的差可近似表示标准差的大小。图中分别用不同颜色标注了不确定性优化过程中的关键节点位置，并在其旁边展示了压力分布的均值和标准差响应结果以及翼型的变化。压力分布图中每一个关键迭代步除了可以和上一关键步对比压力分布均值外，还可以始终与初始翼型对比压力分布均值和标准差响应范围。

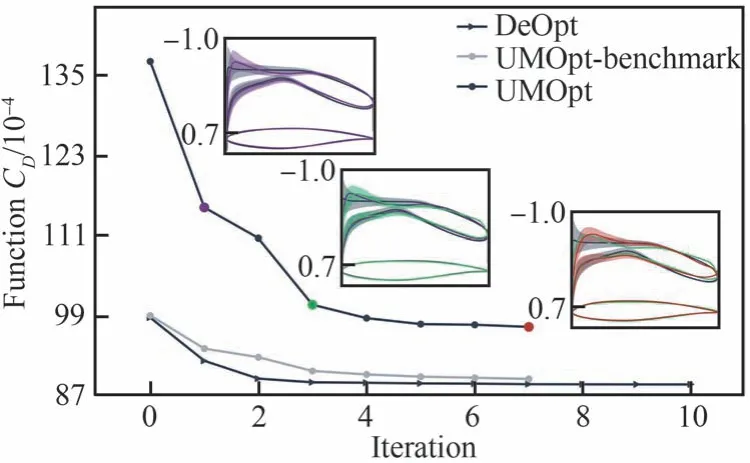
图26 低亚声速确定性及不确定性优化历程（黑色圆形线：DeOpt，确定性优化目标函数变化；黑色三角线：UMOpt，不确定性优化目标函数变化；灰色圆形线：UMOpt，不确定性优化中基准流场的阻力系数变化）Fig.26 Low subsonic deterministic and uncertain optimization history（Black circle line： DeOpt，change of objective function in deterministic optimization； black triangle line： UMOpt，change of objective function in uncertainty optimization； gray circle line： UMOpt， change of drag coefficient of mean flow field in uncertainty optimization）

不确定性优化历经主迭代8 次，最终满足约束和目标函数收敛条件。优化过程中前几步主迭代目标函数下降明显，而最后几步目标函数变化较小，主要完成的是对压力分布的调整和光顺，优化过程中阻力系数标准差大幅减小。不确定性优化设计主要的优化方向为小幅提高上表面头部吸力峰峰值，并不断推迟吸力峰出现的位置；降低下表面的顺压梯度。优化的最终结果UMOpt 翼型基准场阻力系数略大于DeOpt 翼型，但在翼型头部附近的标准差响应明显小于DeOpt 翼型。

5.2 跨声速翼型优化设计

初始翼型选择RAE2822，设计状态参考Honda Jet，Ma= 0.70，Re= 7.93×106，CL=0.38。FFD 控制框与低亚声速状态下保持一致，即图21 所示。对于该翼型分别进行单点确定性优化设计和考虑马赫数和迎角不确定性的优化设计。定义如式（36）所示的优化问题。相比于低亚声速优化增加力矩约束以控制低头力矩。

在考虑马赫数和迎角不确定性的优化中假设马赫数和迎角分别满足Ma～N(0.70，(0.05)2)和α～N(0.387，(1.0)2)的正态分布，此时均值状态下翼型升力系数为0.38。根据PCE 验证结果，在跨声速优化设计中选择使用3 阶梯度增强型多项式混沌法，可将误差控制在1%以下。

表6 给出了跨声速翼型优化的确定性和不确定性力系数结果，其中各确定性的力系数为基准流场结果，即Ma=μ(Ma)，α=μ(α)。UMOpt翼型确定性基准场阻力略大于DeOpt 翼型，但从不确定性结果上看UMOpt 翼型的阻力系数均值（89.19 counts）相比于初始翼型减少约6%，略小于DeOpt 翼型的阻力系数均值（91.44 counts）。在阻力系数标准差响应上，差异更加明显，UMOpt 翼型仅为1.6 counts，与初始翼型相当。而DeOpt 翼型的阻力系数标准差为5.11 counts，甚至高于初始翼型，表明仅考虑确定性性能的优化结果有可能导致性能鲁棒性变差。

表6 跨声速翼型优化结果（阻力系数单位为counts）Table 6 Transonic airfoil optimization results （Drag coefficient in counts）

图27 和图28 分别为确定性优化和不确定性优化的翼型结果对比和压力分布对比。DeOpt翼型头部半径变大，上表面最大厚度位置前移，下表面前缘厚度变小。相应的压力分布上表面吸力峰增大。为了满足力矩约束，后缘被卸载，原本的后加载被消除，升力载荷向头部移动。

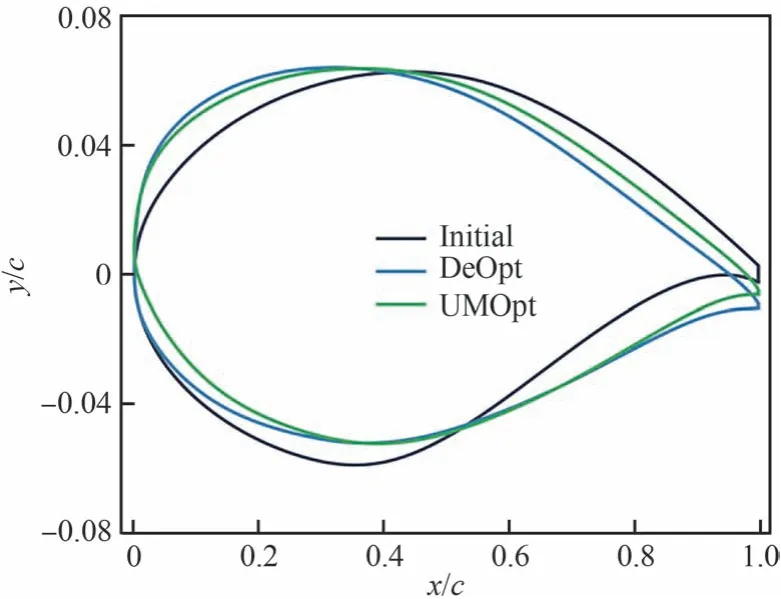
图27 跨声速确定性及不确定性优化翼型对比Fig.27 Comparison of transonic deterministic and uncertain optimal airfoils

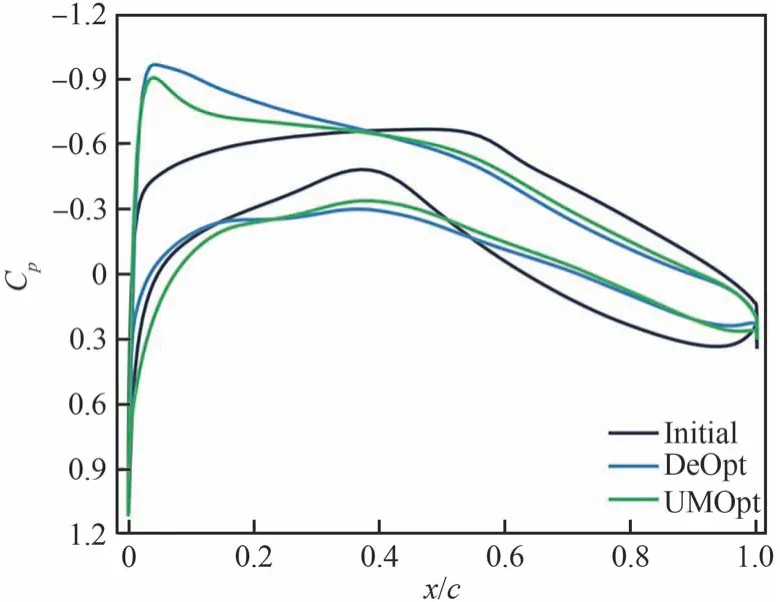
图28 跨声速确定性及不确定性优化压力分布对比Fig.28 Comparison of transonic deterministic and uncertain optimal pressure distribution

从图29 所示的小提琴图中可以看出，UMOpt 翼型具有明显优势。DeOpt 翼型在马赫数和迎角的不确定性扰动下具有比初始翼型更差的阻力性能鲁棒性。相比之下，UMOpt 翼型在保持初始构型鲁棒性基本不变的情况下进一步降低了阻力系数的平均值。

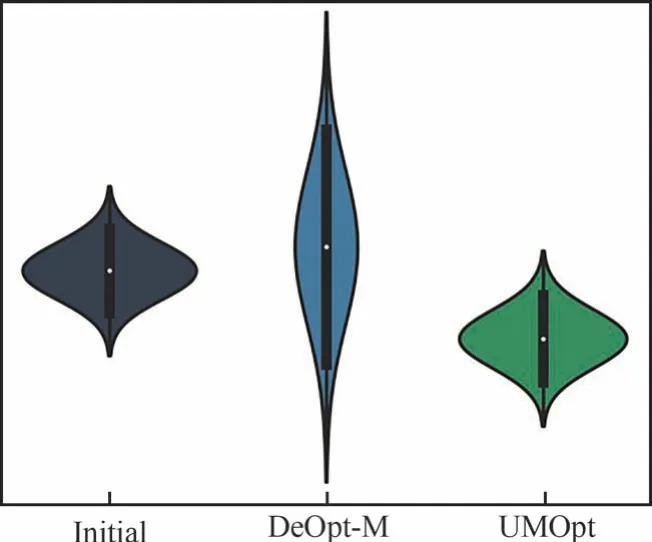
图29 跨声速确定性及不确定性优化Fig.29 Random distribution of drag coefficients for transonic deterministic and uncertain optimization

跨声速确定性和不确定性优化历程如图30所示，不确定性优化历经主迭代8 次，最终满足约束和目标函数收敛条件。优化历程中前半程目标函数下降较快，后半程目标函数变化较小，主要完成的是对压力分布的调整和光顺，优化过程中阻力系数标准差变化较小，说明全湍流考虑马赫数和迎角不确定性的优化仅降低了平均阻力性能，未明显优化鲁棒性。不确定性优化设计主要的优化方向是不断提高头部吸力峰值，减小后部的升力载荷，将载荷向前缘移动。

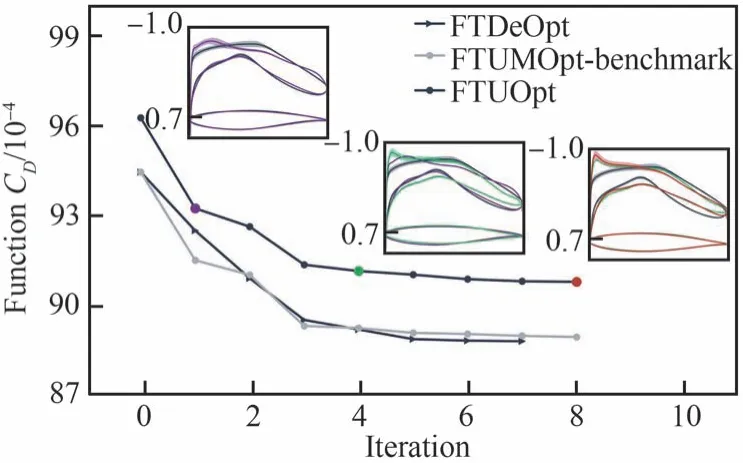
图30 跨声速确定性及不确定性优化历程（黑色圆形线：DeOpt，确定性优化目标函数变化；黑色三角线：UMOpt，不确定性优化目标函数变化；灰色圆形线：UMOpt，不确定性优化中基准流场的阻力系数变化）Fig.30 Transonic deterministic and uncertain optimization history（Black circle line： DeOpt， change of objective function in deterministic optimization；black triangle line： UMOpt， change of objective function in uncertainty optimization； gray circle line： UMOpt， change of drag coefficient of mean flow field in uncertainty optimization）

6 结 论

基于非嵌入式多项式混沌法并结合伴随方程法建立了高效、可靠的基于梯度算法的不确定性优化设计方法，相关研究总结如下：

1）利用伴随方程法求得的导数信息发展了一种梯度增强型多项式混沌法，实现了高效精确的不确定性分析。通过亚声速和跨声速二维翼型的不确定性分析算例验证了所使用的梯度增强型多项式混沌法的精度。其可对力系数、空间流场压力分布的不确定性响应进行较为全面而准确的预测。

2）利用基于方差分解的全局敏感性分析方法对亚声速和跨声速二维翼型不确定性分析算例中不确定性变量的敏感性进行量化。结果表明，前后缘的条状区域常受到马赫数不确定性的影响，驻点附近的流场压力系数常受到迎角不确定性的影响。亚声速状态下对流场不确定性响应产生主要影响的是迎角；对于存在激波的跨声速流场，对流场压力系数标准差贡献最大的是马赫数。

3）基于梯度增强型多项式混沌法、FFD 参数化方法、IDW 动网格方法和SNOPT 优化算法搭建了不确定性梯度优化设计框架。利用该框架分别对低亚声速二维翼型、跨声速二维翼型进行考虑马赫数和迎角不确定性的优化设计。

4）优化结果表明，只考虑确定性性能的优化设计有可能导致不确定性条件下性能的降低，而考虑不确定性的优化设计相比于确定性优化设计能够显著提高翼型抵抗马赫数和迎角扰动的能力，同时减小阻力均值和标准差，分别可达到约17%和80%。

研究结论表明，所建立的梯度增强型多项式混沌法以及与伴随理论耦合的不确定性梯度优化设计系统可以应用于具有大规模确定性设计变量和少量不确定性变量的气动鲁棒优化设计。