喻陈波，杨 鹏

（辽宁科技大学 理学院，辽宁 鞍山 114051）

1356年，印度数学家Narayana在他的名著《Ganita Kaumudi》中提出牛群问题：“小牛在其出生后的第4年每年生产一只小牛，问20年后总计有多少只牛？”［1］这是一个类似Fibonacci兔子的问题，容易算出前几年牛群中的牛数为：1，1，1，2，3，4，6，9，13，19，…。人们常称这个数列为奶牛数或Narayana奶牛数，而Narayana数则是另一个数列。和Fibonacci数列不同的是，奶牛数是一个三阶递归数列，满足递归关系

其初始项为N0=0，N1=N2=1。

纯位数是十进制展开中的每一位都是同一个数的正整数。因此，小于10的正整数都是纯位数。除此之外，11、22、33、44、…等也都是纯位数。对于大于10的纯位数，Luca［2］于2000年首次证明Fibonacci数和Lucas数中仅有11和55是纯位数。之后，与数列中的纯位数相关的研究大量涌现。Faye等［3］证明Pell数均不是纯位数。2018年，Rayaguru等［4］证明除数位中出现6的情形，Balancing数均不是纯位数。2020年，Bravo等［5］证明奶牛数中仅55是纯位数，并得到更一般的结果：没有位数超过6的纯位数是两个奶牛数的和。2022年，Ji等［6］证明最大的可表为多个连续奶牛数乘积的纯位数为88。

本文主要寻找所有可表为两个奶牛数之差的纯位数。由于纯位数可表示为的形式，当n＞max{10,m}时，有

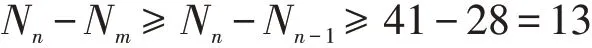
因此，问题等价于求解丢番图方程

其中n≥m，l≥2。不同于Fibonacci数，作为三阶递归数列，奶牛数没有二阶递归数列那样较好的性质。本文主要通过代数数的对数线性型的下界及Baker-Davenport缩减方法，结合Mathematica计算丢番图方程（1）的所有解。

1 奶牛数的基本性质

奶牛数{Nn}n≥0的特征方程是

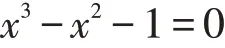
该方程有一个实根和两个共轭复根，它们分别是

引理1［5］设{Nn}n≥0为奶牛数，则有：

（1）对任意的n≥1，αn-2≤Nn≤αn-1；

（2）对任意的n≥0，奶牛数满足Binet公式

其中

（3）若记en=cβ βn+2+cγγn+2，则对任意的n≥1有

为了求解丢番图方程（1），需要引入一些超越方法。设γ是数域Q上的d次代数数，其在Z上的最小多项式为的绝对对数高

引理2对数高h的性质：

（1）h(η±γ)≤h(η)+h(γ)+log 2；

（2）h(ηγ±1)≤h(η)+h(γ)；

（3）h(ηs)=|s|h(η),s∈Z。

Matveev定理［7］可以给出丢番图方程（1）一个较大的上界。

引理3［7］设K为有理数域Q上的D次扩域，γ1,…,γt为K上的正实数，b1,…,bt为有理整数。令

及

若Λ≠0，则有

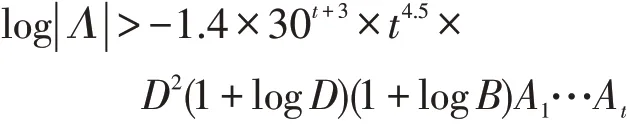
采用Bravo等［8］给出的上界缩减方法，给出一个实际可计算的上界。这个方法是Dujella等［9］给出的Baker-Davenport定理推广的变形。

引理4［8］设A,B,γ̂,μ̂为正实数，M为正整数，p/q为无理数γ̂的收敛子，且满足q＞6M。记若∊＞0，则在

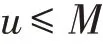
及

的条件下，不等式

对(u,v,w)无整数解。

引理5［10］设整数m≥1，实数x,T满足T＞(2m)2m，x＜Tlogmx，则x＜2mTlogmT。

2 丢番图方程（1）的一个较大上界

引理6若n≥11时丢番图方程（1）有解，则

证明若n=m，则方程（1）有解l=0。但这不满足方程（1）对l的要求。因此不妨设n＞m且n≥11。若方程（1）有解，则

及

由式（2）和式（3）得

又

所以由式（4）可得

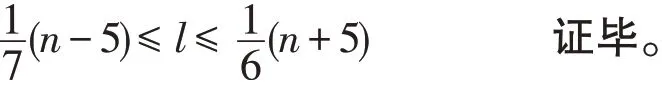
定理1若丢番图方程（1）有解，则n＜5.2×1031。

证明若方程（1）有解，则由引理1得

等式（5）两边同除以cααn+2并取绝对值，得到

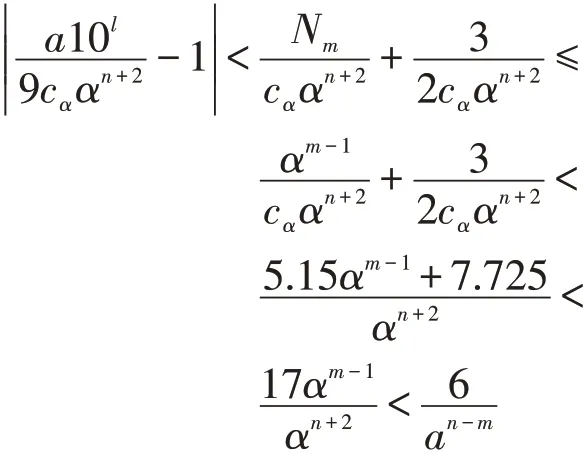
由于γ1,γ2,γ3∈K=Q(α)，因此取D=［K：Q］=3。由对数高的定义式得

及

故取A1=logα，A2=3 log 10。又cα在Z上的最小多项式为31x3-31x2+10x-1，由引理2得

于是取A3=12 log 3。由引理6可知max{n+2,l,1}=n+2，故取B=n+2。

为了利用引理3给出方程（1）的一个较大的上界，还需验证Λ1≠0。假设Λ1=0，则有

设G为α的最小多项式在Q上的分裂域的Galois群，σ∈G为满足σ(α)=β的自同构，将σ作用在式（7）上，得到

若取n≥5，则有1+log(n+2)≤2 logn。由不等式（6）和式（8）得到

为了给出n的独立于m的上界，还需再应用一次引理3。方程（1）还可以写成

因为n＞m，所以αn+2-αm+2≠0。式（10）两边同除以cααn+2(1+αm-n)，取绝对值得

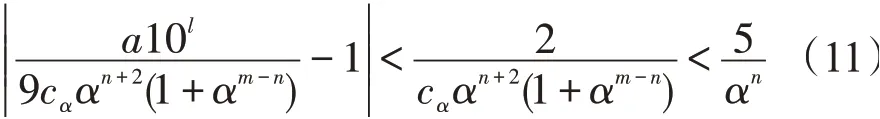
若Λ2=0，则有

类似的，将σ作用在式（13）上，得到

但

而当l≥2时，a10l/9＞10，矛盾。故有Λ1≠0。又由引理2得

因此，由式（9）得

故可取A3=7.7×1013logn。于是，由引理3得到的第2个界

结合式(12)得

因此

从而由引理5得到n＜5.2×1031。

3 丢番图方程（1）的一个可计算上界

定理1已经给出丢番图方程的解的上界，但用这个界来寻找方程（1）的解所需要搜索数组(n,m,a,l)的个数超过了可观测宇宙中的所有原子总数1082。因此，还需要将这个界大幅地缩小。幸运的是，方程（1）可以利用无理数的逼近性质，即引理4来处理这个问题。

定理2若丢番图方程（1）有解，则n-m≤222。

证明取

因为eΓ1-1=Λ1≠0，所以Γ1≠0。若Γ1＞0，则有

若Γ1＜0，则当n-m≥2时，由式（2）和式（5）及引理1有

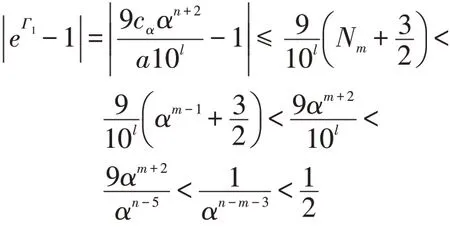
于是e-Γ1＜2。从而

总之，在任何情况下，都有

两边同除以logα得到

满足q65＞6M且∊a＞0.034 212＞0，a=1,2,…,9。这时，对每个a有

因此由引理4得n-m≤222。证毕。

为了给出独立于m的上界，还需要再应用一次引理4。

定理3若丢番图方程（1）有解，则n≤244。

证明类似定理2的证明过程。取

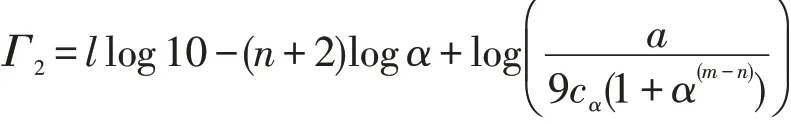
因为eΓ2-1=Λ2≠0，所以Γ2≠0。若Γ2＞0，则有

若Γ2＜0，则当n≥15时，由式（2）和式（10）及引理1有

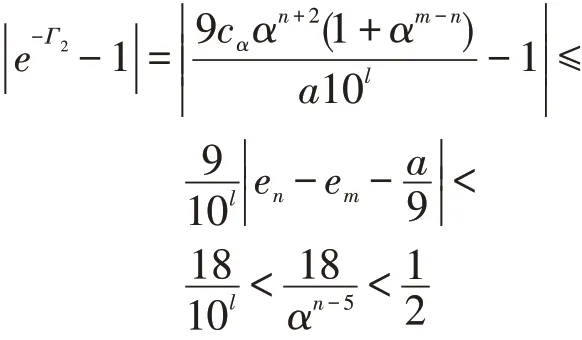
于是e-Γ2＜2。从而

总之，在任何情况下，都有

两边同除以logα得到

满 足q70＞6M且 对n-m≤222有∊a,n-m＞0.000 195 552＞0，a=1,2,…,9。这时，对每个a有

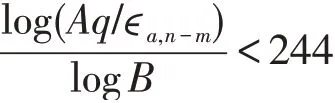
因此由引理4得n≤244。证毕。

4 丢番图方程（1）的所有解

由定理3可知，若方程（1）有解，则m＜n≤244。再由引理6得l≤41。利用Mathematica软件经简单的搜索得到方程（1）的所有解，计算耗时仅0.171 875 s。

定理4丢番图方程

的所有解为

5 结论

利用对数线性型及缩减方法，研究可表为两个奶牛数之差的纯位数。在可计算的解的上界中搜索，给出所有可表为两个奶牛数之差的纯位数，其中最大的形如两个奶牛数之差的纯位数是88。文中所使用的方法可以进一步应用在寻找可表为给定递归数列的线性组合的纯位数等与递归数列及纯位数有关的问题中。