徐保根，郑萌萌，兰 婷

（华东交通大学理学院，江西 南昌 330013）

图论中的简单图可分为无向简单图和有向简单图，我们在本文中只讨论无向简单图。 连接两个相同顶点的边， 这种边的条数就称为边的重数，当重数大于1 时的边就称为重边。 端点重合为一点的边则称为环。 若一个图中每条边都无方向时，则称为无向图。 当一个图没有环也没有重边且每条边都是无方向时则称此图为无向简单图。 研究中未说明的术语和符号与邦迪等[1-4]相同。

图论中的比较重要的内容是图的控制理论，其研究的内容也越来越广泛。 赵利芬[5]，孟卓明[6]从最小边度出发对图的边控制以及边控制集的相关参数进行了深一步的研究，得到了几类特殊图的集边控制数，其方法对于同类结构图形的参数求解具有一定的启发意义， 但是不适用于具有强对称性的图。 图的控制理论方面的主要研究成果被Haynes等[7-9]所叙述，图的控制划分数的具体概念被Cockayne 等[10]所引入，图的集边控制数最早是被Zelinka在1983 年所研究，在Zelinka[11-14]的文献中从图的最大度以及最大边度进行考虑，给出了任意图的集边控制数的最好界限，并且利用此界限及反证法从而获得了几类特殊图的集边控制数。 在求解图的集边控制数时，Zelinka 运用的最好界限确实对于研究边控制集划分问题提供了很好的分析思路，但是对于具有强对称性的图，仅仅依靠这种方法只能得到强对称图的划分规律，但是无法得出具体的集边控制数，基于此现状，本文提出了一种创新的方法来弥补前人研究的不足，研究通过参考几类图的边控制集划分的方法[15-17]，然后针对具有强对称性的图研究以全新的角度对此类图的边控制集划分进行了初步探索。 轮图是典型的强对称图形，对于物理，化学，计算机网络等领域的研究具有重大的理论价值与应用价值。 该项研究根据轮图的强对称性按照两种不同的划分方法将轮图所有边两两划分成对应的几个集合，每个集合由两条相邻的边组成，且集合之间互不相交，根据集边控制数的定义和集合之间的对应关系来确定相等边元素的几种情况，再进行分类讨论推理，最后利用反证法进而确定了轮图的集边控制数。Wn+1=Cn∨K1（图1）表示n+1 阶轮图。

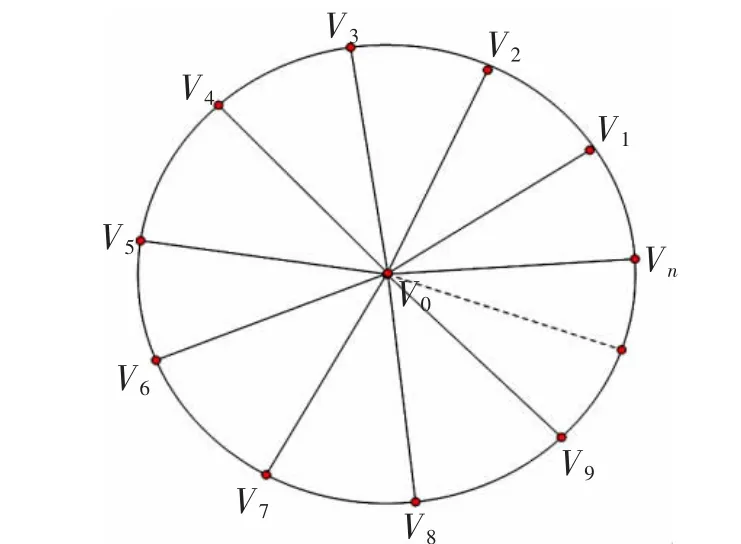
图1 轮图Fig.1 Wheel graphs

1 定义及引理

定义1设G=（V，E） 为一个非空图，D⊆E，若对任何一条边∀e∈E-D,都存在e′∈D，使得e′和e相邻(即有一个公共点)，则称D 为图G 的一个边控制集。

定义2对于非空图G=（V，E）， 若有划分E＝使任意Di（i=1，2，…，t）都是图G 的边控制集，则把这样的划分叫作图G 一个t-集边控制划分。把图G 的集边控制数记作d（G），定义

定义3设G=（V，E）为一个图，e∈E，则NG（e）表示G 中与e 相邻的边集，称为e 的边邻域，NG（e）=NG（e）∪{e}为e 的闭边邻域。 dG（e）=|NG（e）|表示e在G 中的边度，δe（G）=min dG（e）。 NG［e］、NG（e）和dG（e）可分别简记为N[e]，N（e），d（e）。 若e=uv∈E（G）,则有

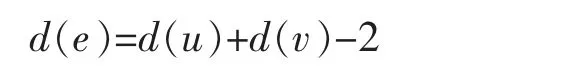
引理1对于任何图G，δ（G）和δe（G）分别表示图G 的最小度和最小边度，则有

引理2对于n+1 阶轮图， 则有γ′（Wn+1）=]，n≥3。

2 主要结果及证明

定理1对于轮图Wn+1， 设n≥3 且n 为整数，则有

证明令G＝Wn+1，可记K1中的点为V0，圈Cn上的点V（Cn）={vi|1≤i≤n}，E（Wn+1）={v0vi|1≤i≤n}∪{vivi+1|1≤i≤n}。

易知δe（Wn+1）=4，由引理1 可知d′（Wn+1）≤5。下面分别定义Wn+1的边标号函数f，并将E（Wn+1）划分成若干个边控制集Di={e∈E （G）｜f （e）=i}（i=1，2，3，4，5）。令f（v0vi）＝yi-1，f（vivi+1）＝xi，Ai={xi，yi}，Bi={xi，yi-1}，i=1，2，3，…，n。 下标取模n 最小正剩余。

若d′（Wn+1）=5， 则 {x2，x3，y2}∪A1={x2，x3，y2}∪B4={1，2，3，4，5}，所以A1=B4，以此类推可得A1=Bi+3，下标取模n 最小正剩余。 易知N[v2v3]={x1，x2，x3，y1，y2}={1，2，3，4，5}。 因为，x1∈A1，A1=B4，则x1∈B4，又已知B4＝{x4，y3}， 所以x1=x4或y3。 因为x4∈A4，A4=B7，则x4∈B7，又已知B7＝{x7，y6}，所以x4=x7或y6。 因为y3∈A3，A3=B6，则y3∈B6，又已知B6={x6，y5}，所以y3=x6或y5。 以此类推可以得到关于x1的标号函数递推图， 同理可以得到x2，x3，y1，y2的标号函数递推图，其中xi与yi的标号函数递推图是相同的，展示x1，x2，x3的标号函数递推图依次如图2～图4 所示。

图2 x1 的标号函数递推图Fig.2 Labeled function recursion graph of x1

图3 x2 的标号函数递推图Fig.3 Labeled function recursion graph of x2

图4 x3 的标号函数递推图Fig.4 Labeled function recursion graph of x3

下 面 分 别 对 与x1，x2，x3，y1，y2函 数 值 相 同 的 边进行分析。

1） x1∈B1，An-2=B1且An-2={xn-2，yn-2}，所以x1=yn-2或者x1=xn-2，又因为B2，B3，Bn中一定不含有与x1函数值相同的边，则Bn-1与Bn+1，或者Bn-2与Bn+1中一定含有与x1函数值相同的边。

2） x2∈B2，An-1=B2且An-1={xn-1，yn-1}，所以x2=yn-1或者x2=xn-1，又因为B1，B3，B4中一定不含有与x2函数值相同的边，则Bn与Bn+2，或者Bn-1与Bn+2中一定含有与x2函数值相同的边。

3） x3∈B3，An=B3且An={xn，yn}， 所以x3=yn或者x3=xn，又因为B2，B4，B5中一定不含有与x3函数值相同的边，则Bn+1与Bn+3，或者Bn与Bn+3中一定含有与x3函数值相同的边。

4） y1∈B2，An-1=B2且An-1={xn-1，yn-1}，所以y1=yn-1或者y1=xn-1，又因为B1，B3，B5中一定不含有与y1函数值相同的边，则Bn与Bn+2，或者Bn-1与Bn+2中一定含有与y1函数值相同的边。

5） y2∈B3，An=B3且An={xn，yn}， 所以y2=yn或者y2=xn，又因为B2，B4，B6，中一定不含有与y2函数值相同的边，则Bn+1与Bn+3，或者Bn与Bn+3中一定含有与y2函数值相同的边。

情况1当n=0（mod 6）时，令n=6k。

子情况1.1当k=1 时，n=6。 反证法：假设d′（Wn+1）=5， 则此时只有B4，B7中含有与x1函数值相同的边， 结合x1的标号函数递推图可知与x1函数值相同的边只有x4，即{x1，x4}为一个边控制集，但此时y2却不受此控制集的控制，产生矛盾，所以假设有误，故d′（Wn+1）≤4。 定义标号函数f 如下

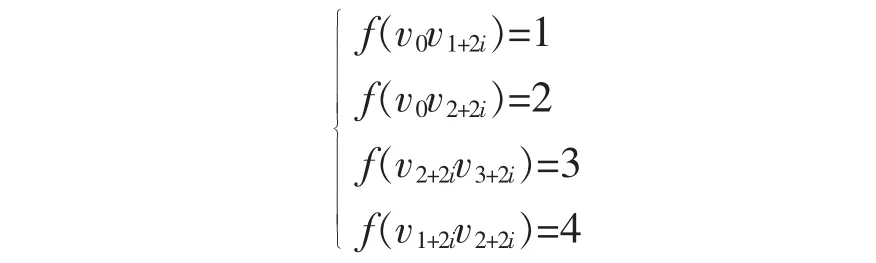
式中：i=0，1，2；下标取模n 最小正剩余。 可见当n=6时，E（Wn+1）=，且每个Di均为Wn+1的边控制集，由集边控制数定义可知d′（Wn+1）≥4。 又已知d′（Wn+1）≤4，所以当n=6 时，d′（Wn+1）=4。

子情况1.2当k=2 时，n=12。 反证法：假设d′（Wn+1）=5， 则根据之前对x1，x2，x3，y1，y2的函数值的分析可知。

1） x1=y10或者x1=x10， 则B11与B13， 或者B10与B13中一定含有与x1函数值相同的边， 则与x1函数值相同的边有如下几种可能：

2） x2=y11或者x2=x11， 则B12与B14， 或者B11与B14中一定含有与x2函数值相同的边， 则与x2函数值相同的边有如下几种可能：

3） x3=y12或者x3=x12， 则B13与B15， 或者B12与B15中一定含有与x3函数值相同的边， 则与x3函数值相同的边有如下几种可能：

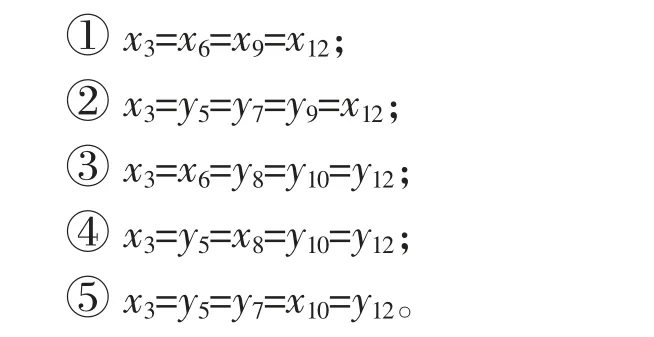
4） y1=y11或者y1=x11， 则B12与B14， 或者B11与B14中一定含有与y1函数值相同的边， 则与y1函数值相同的边有如下几种可能：

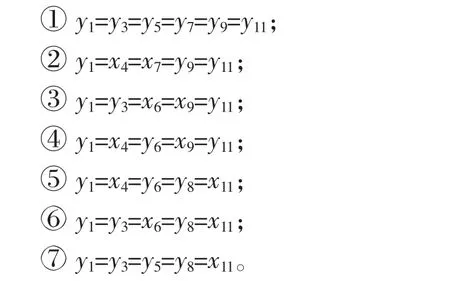
5） y2=y12或者y2=x12， 则B13与B15， 或者B12与B15中一定含有与y2函数值相同的边， 则与y2函数值相同的边有如下几种可能：

由于x1，x2，x3，y1，y2的函数值各不相同，所以当n=12 时，无论x1，x2，x3，y1，y2的函数值为上述5 种可能里的哪一种组合，最终都会产生矛盾，所以假设有误，故d′（Wn+1）≤4，定义标号函数f 如下

式中：i=1，2，3，4，5；下标取模n 最小正剩余。可见当n=12 时，E（Wn+1)=，且每个Di均为Wn+1的边控制集，由集边控制数定义可知d′（Wn+1)≥4。 又已知d′（Wn+1)≤4，所以当n=12 时，d′（Wn+1)=4。

子情况1.3当k≥3 时，定义标号函数f 如下

图5 W19 的标号函数Fig.5 Labeled function of W19

情况2当n=1（mod6）时，令n=6k+1。

子情况2.1当k=1 时，n=7。 反证法：假设，d′（Wn+1)=5，则x1=y5或者x1=x5，则B6与B8，或者B5与B8中一定含有与x1函数值相同的边。 由x1标号函数递推图可知， 只有B4，B6， 与B8中一定含有与x1函数值相同的边, 即x1=y3=y5。 以此类推可知B4，B7与B9中一定含有与y1函数值相同的边， 即y1=x4=y6。B5，B7与B9中一定含有与x2函数值相同的边，即x2=y4=y6。 则得出y1=x2，又N［v2v3］＝｛x1，x2，x3，y1，y2｝=｛1，2，3，4，5｝，产生矛盾，所以假设有误，故d′（Wn+1)≤4。 定义标号函数f 如下

可见当n=7 时，E（Wn+1）=，且每个Di均为Wn+1的边控制集， 由集边控制数定义可知d′（Wn+1）≥4。 又已知d′（Wn+1）≤4，所以当n=7 时，d′（Wn+1）=4。

子情况2.1当k≥2 时，定义标号函数f 如下

图6 W14 的标号函数Fig.6 Labeled function of W14

情况3当n=2 （mod6） 时， 令n=6k+2，（k＝1，2，3，…）。 定义标号函数f 如下

图7 W9 的标号函数Fig.7 Labeled function of W9

情况4当n≡3（mod6）时，令n=6k+3。

子情况4.1当k=0 时，n=3。 反证法： 假设d′（Wn+1）=5，则N[v1v2]=N[v2v3]={1，2，3，4，5}又因为N[v1v2]={x1，x2，x3，y1，y3}，N[v2v3]={x1，x2，x3，y1，y3}，所以y2=y3，已知y2与y3都属于N[v1v2]，又因为当d′（Wn+1）=5 时，轮图的每个闭边邻域内的元素都各不相同，产生矛盾。 所以假设有误，故d′（Wn+1）≤4。

假设d′（Wn+1）=4，即E（Wn+1）=D1∪D2∪D3∪D4，且Di（i=1，2，3，4）均为图Wn+1的边控制集，则必存在某个Di，使

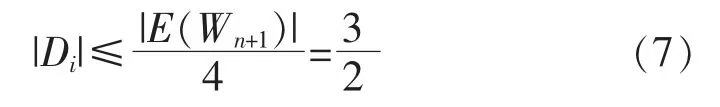
即

由图Wn+1的边控制数的定义知，γ′（Wn+1）=min|Di|≤]=1，由引理2 知，γ′（Wn+1）=]=]=2，但是]＜]，即 存 在某个Di，使 得|Di|＜γ′（Wn+1），产生矛盾，所以假设有误，故d′（Wn+1）≤3。定义标号函数f 如下

可见E（Wn+1）=，且每个Di均为Wn+1的边控制集，由集边控制数的定义可知d′（Wn+1）≥3。 又已知d′（Wn+1）≤3，所以当n=3 时，d′（Wn+1）=3。

子情况4.2当k=1 时，n=9。 反证法： 假设d′（Wn+1）=5，则根据之前对x1，x2，x3，y1，y3的函数值的分析可知。

1） x1=y7或者x1=x7，则B8与B10，或者B7与B10中一定含有与x1函数值相同的边，即x1=y3=y5=y7或者x1=x4=x7。

2） x2=y8或者x2=x8，则B9与B11，或者B8与B11中一定含有与x2函数值相同的边，即x2=y4=y6=y8或者x2=x5=x8。

3） x3=y9或者x3=x9，则B10与B12，或者B9与B12中一定含有与x3函数值相同的边，即x3=y5=y7=y9或者x3=x6=x9。

4） y1=y8或者y1=x8，则B9与B11，或者B8与B11中一定含有与y1函数值相同的边，即y1=y3=x6=y8或者y1=x4=y6=y8或者y1=y3=y7=y9。

5） y2=y9或者y2=x9，则B10与B12，或者B9与B12中一定含有与y2函数值相同的边，即y2=y4=y6=x9或者y2=x5=y7=y9或者y2=y4=y7=y9。

由于x1，x2，x3，y1，y2的函数值各不相同，所以当n=9 时， 无论x1，x2，x3，y1，y2的函数值为上述5 种可能里的哪一种组合，最终都会产生矛盾。 所以假设有误，故d′（Wn+1）≤4，定义标号函数f 如下

式中：i=0，1，2。 可见当n=9 时，E（Wn+1）=，且每个Di均为Wn+1的边控制集， 由集边控制数定义可知d′（Wn+1）≥4。 又已知d′（Wn+1）≤4， 所以当n=9时，d′（Wn+1）=4。

子情况4.3当k≥2 时。 定义标号函数f 如下

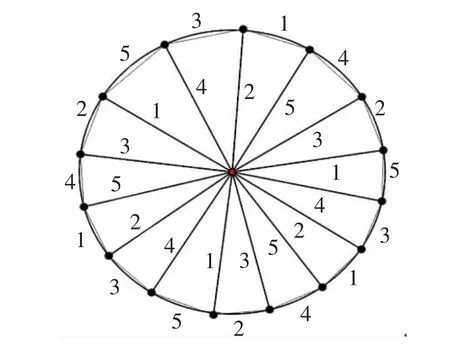
图8 W16 的标号函数Fig.8 Labeled function of W16

情况5当n≡4（mod6）时，令n=6k+4。

子情况5.1当k=0 时，n=4。 则有N[v1v2]={x1，x2，x4，y1，y4}，N[v1v4]={x1，x3，x4，y3，y4}。 反证法：假设d′（Wn+1）＝5，则对于任意的e∈E（Wn+1），都有N[e]={1，2，3，4，5}，但又因为A1＝B4，即{x1，y1}={x4，y3}，所以y3=x1或y3=y1。 又因为y3，x1∈N[v1v4]，所以y3≠x1，故只有y3=y1。 又由于N[v1v2]=N[v1v4]，即{x1，x2，x4，y1，y4}={x1，x3，x4，y3，y4}，所 以x2=x3，但是x2，x3∈N[v2v3]，当d′（Wn+1）=5 时，轮图的每个闭边邻域内的元素都各不相同；因此x2≠x3，产生矛盾，所以假设有误，故d′（Wn+1）≤4。 定义标号函数f 如下

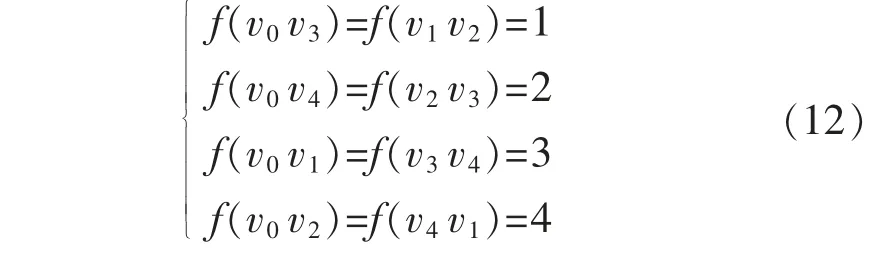
可见E（Wn+1）=，且每个Di均为Wn+1的边控制集，由集边控制数定义可知d′（Wn+1）≥4。 又已知d′（Wn+1）≤4，所以当n=4 时，d′（Wn+1）=4。

子情况5.2当k≥1 时定义标号函数f 如下

图9 W11 的标号函数Fig.9 Labeled function of W11

情况6当n≡5（mod6）时，令n=6k+5。 （k=0，1，2，…）定义标号函数f 如下

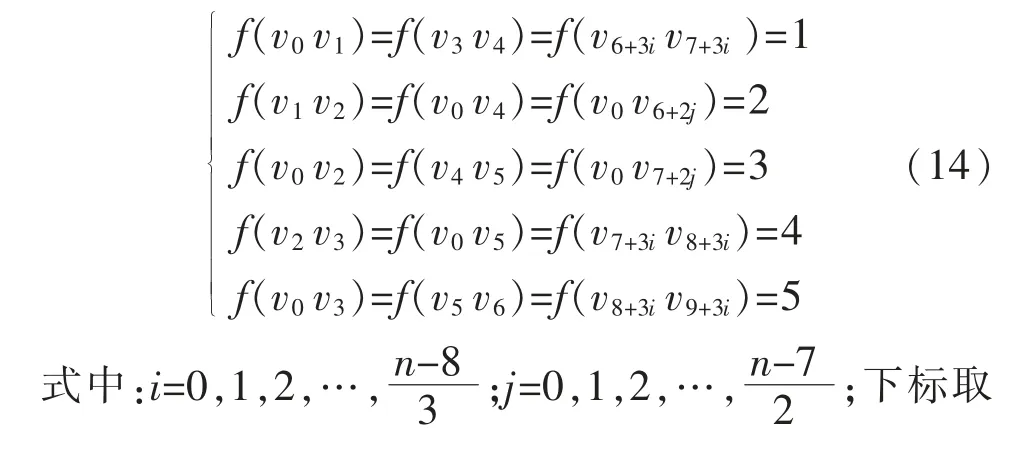
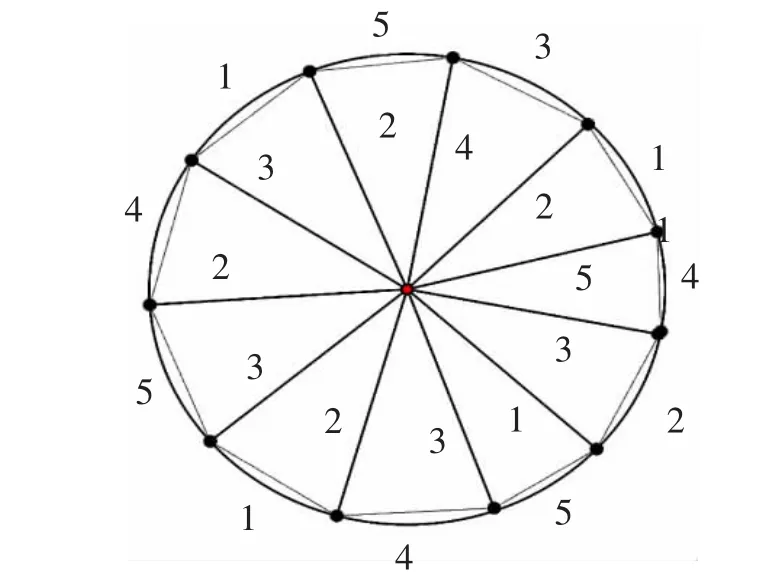
图10 W11 的标号函数Fig.10 Labeled function of W11

定理证毕。

3 结论

轮图作为一类具有强对称性的复合图类，有着极其重要的理论研究价值和应用价值。

本研究的主要结果是利用归纳递推法确定了具有强对称性图的边控制划分数，获得了轮图Wn+1的集边控制数, 此方法也可以用来探索其他具有对称性图类的边控制集划分问题，对于图的控制领域也具有较好的应用前景。