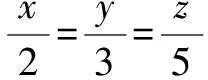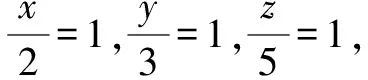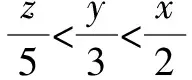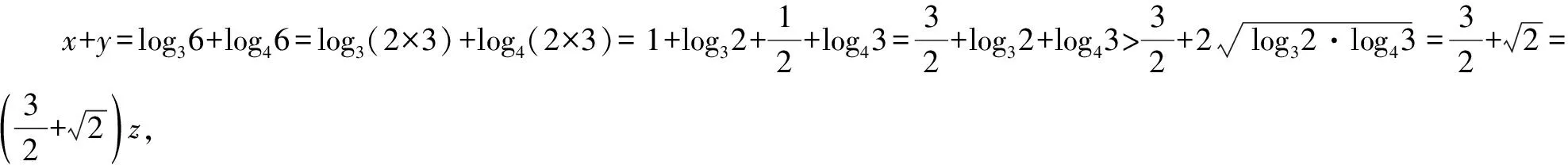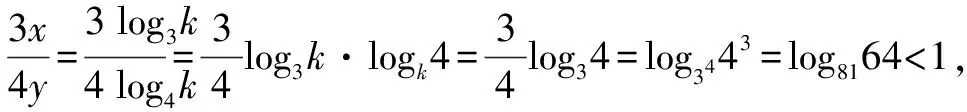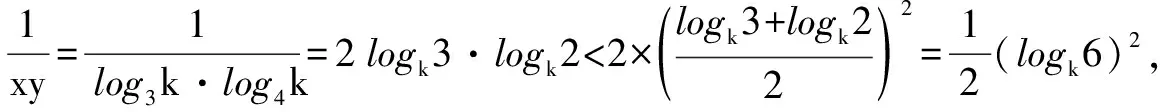⦿甘肃省张家川县第一高级中学 马启荣

比较大小是近年高考数学中经常考查的一类常规题型，侧重考查指数函数、对数函数以及幂函数的图象与性质在解题中的灵活运用，考查学生的运算求解能力以及逻辑推理能力.基于此，笔者着重归纳整理了含有三个变量的指数式连等(或者对数式连等)的大小比较问题，旨在帮助学生灵活运用“特例法”与“设元法”迅速分析、解决此类问题，进而提高解题能力，提升数学核心素养.

1 三个“指数式连等”的大小比较问题

一般地，分析、解决含有三个变量且涉及三个指数式连等的大小比较问题时，常用的解题方法有两种：一是先假定其中的某一个变量的取值为常数，再根据这个变量的取值分析其他两个变量的取值情况，以便灵活运用相关指数运算法则或者其他知识进行大小比较，这种方法称之为“特例法”；二是先对连等式进行换元，即设连等的指数式为某一个参数，再根据指数式与对数式的互化，将指数式转化为对数式，从而便于灵活运用相关对数运算法则或者其他知识进行大小比较，这种方法称之为“设元法”.

例1已知x>0,y>0,z>0，如果2x=3y=5z，那么( ).

A.3y<2x<5zB.2x<3y<5z

C.3y<5z<2xD.5z<2x<3y

解析1：假设z=1，则根据2x=3y=5可得x=log25,y=log35，所以2x=log225

假设y=1，则根据2x=3可得x=log23，所以2x=log29>3y.

综上所述，3y<2x<5z.故选答案：A.

故选答案：A.

2 三个“对数式连等”的大小比较问题

一般地，处理含有三个变量且涉及三个对数式连等的大小比较问题时，常用的解题方法有两种：一是先假定某变量的取值为一个常数，再根据该变量的取值分析其他两个变量的取值情况，以便灵活运用相关对数运算法则或者其他知识进行大小比较，这种方法称之为“特例法”；二是先对连等式进行换元，即设连等的对数式为某一个参数，再根据对数式与指数式的互化，将对数式转化为指数式，从而便于灵活运用相关幂函数的单调性或其他知识进行大小比较，这种方法称之为“设元法”.

第二天看到王祥焦急的模样，老道不慌不忙地给他讲起了生意经。带什么手表的男人是大款，拿什么手袋的女人是富婆；问什么样问题的客人是真心来买古玩，关心什么事宜的客人只是来消磨时间。老道多年来算卦相面的经验用在识人方面自是有一番心得，这时和王祥聊起这个更是得心应手。王祥见老道胸有成竹，也就没再多说什么。

所以应选：B.

温馨提醒，幂函数y=xα在区间(0,+∞)上的单调性可分为以下三种情况：①当α>0时，幂函数y=xα在(0,+∞)上单调递增；②当α=0时，幂函数y=xα(为常数函数)在(0,+∞)上不具有单调性；③当α<0时，幂函数y=xα在(0,+∞)上单调递减.

牛刀小试：(多选题)(2021届江苏省扬州市高三上学期期中考试)已知正数x,y,z满足3x=4y=6z，则下列说法中正确的是( ).

解法1：假设z=1，则根据3x=4y=6可得x=log36,y=log46，则x>1,y>1.

综上所述，应选择：ACD.

解法2：设3x=4y=6z=k，则k>1，且x=log3k,y=log4k,z=log6k.

因为x+y=log3k+log4k

=log6k·log36+log6k·log46

=log6k·(log36+log46)

综上所述，应选择：ACD.

综上，通过上述归类举例解析以及牛刀小试可知，分析、解决涉及三个指数式连等(或者三个对数式连等)的大小比较问题，常用解题方法有“特例法”和“设元法”.对比即知，利用“特例法”解题往往比较简单，便于迅速获解；而运用“设元法”解题需要具有较强的对式子进行化简、变形的能力，同时需要对相关指数函数、对数函数以及幂函数的单调性具有较强的运用能力.总之，希望通过学中“悟”，以达成在“悟”中不断提升解题能力. 诚如此，那么有关涉及指数式连等、对数式连等的大小比较问题，我们真的可以说：Soeasy！