2022年高考数学全国乙卷导数压轴题解析
2022-12-19中央民族大学附属中学呼和浩特分校李雪峰
⦿中央民族大学附属中学呼和浩特分校 李雪峰
1 试题呈现
(2022年高考数学全国乙卷第21题)已知函数f(x)=ln (1+x)+axe-x.
(1)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在区间(-1,0),(0,+∞)各恰有一个零点,求a的取值范围.
2 试题解析
本题的第(1)问不多赘述,下面给出第(2)问的几种不同的思考角度和解题方法.
2.1 思路一及解法
2.1.1 解题思路一的形成
因为题中所给条件是函数零点问题,所以我们先观察函数值的正负情况以及何时为零.
当a≥0时,若x>0,则f(x)=ln (1+x)+axe-x>0恒成立,与题意不符.因此,下面只讨论a<0时的情形.
通过观察易知f(0)=0,当x→-1时,f(x)→-∞;当x→+∞时,f(x)→+∞.要使f(x)在区间(-1,0),(0,+∞)各恰有一个零点,则可以猜测f(x)的图象大致如图1所示.
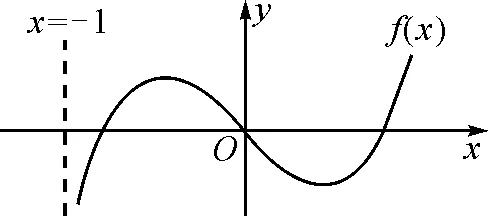
图1
由图1可知,f′(0)=a+1<0显然为其必要条件,即a<-1.下面需要说明:①当a≥-1时,不符合题意;② 当a<-1时,讨论函数f(x)的单调性,再根据零点存在定理说明在区间 (-1,0)和(0,+∞) 上各恰有一个零点.
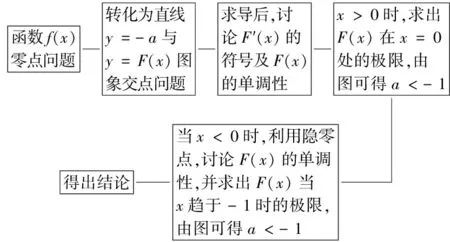
思路一的思维导图如图2所示.
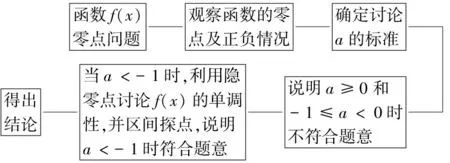
图2
2.1.2 具体解法
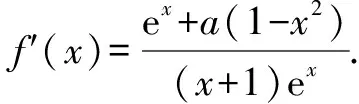
设g(x)=ex+a(1-x2).
当-1≤a<0时,在区间(0,+∞)上,有
g(x)=ex+a(1-x2)=(ex+a)-ax2>0.
所以,在区间(0,+∞)上,f′(x)>0,f(x)单调递增,则f(x)>f(0)=0,这与题意不符.
当a<-1时,g′(x)=ex-2ax,因为g″(x)=ex-2a>0,所以g′(x)在区间(-1,+∞)上单调递增.
又因为g′(-1)=e-1+2a<0,g′(0)=1>0,所以存在唯一x0∈(-1,0),使g′(x0)=0.
因此,当x∈(-1,x0)时,g′(x)<0,g(x)单调递减;当x∈(x0,+∞)时,g′(x)>0,g(x)单调递增.
(为直观起见,下面分别画出函数g′(x),g(x),f(x)的大致图象,如图3~5所示.)
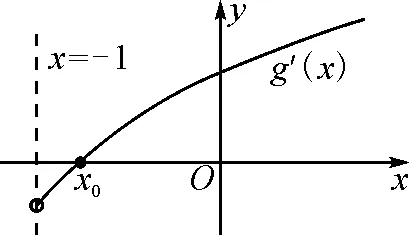
图3
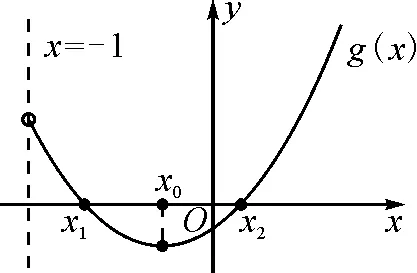
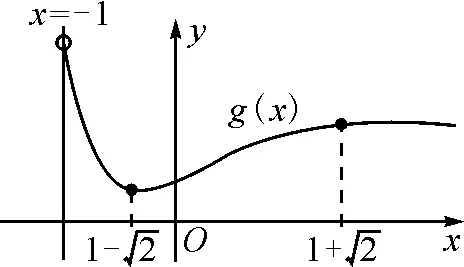
图4
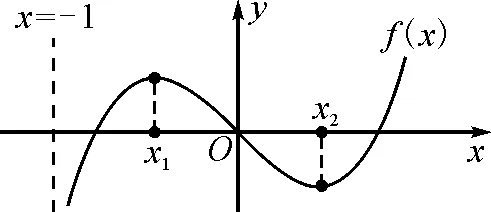
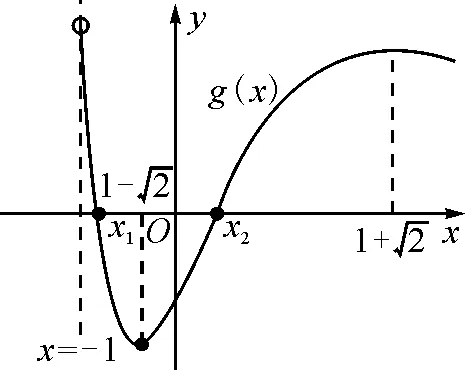
图5
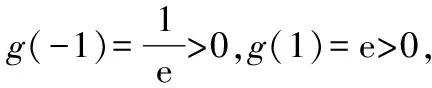
当x∈(-1,x1)时,g(x)>0,f′(x)>0,f(x)单调递增;当x∈(x1,x2)时,g(x)<0,f′(x)<0,f(x)单调递减;当x∈(x2,+∞)时,g(x)>0,f′(x)>0,f(x)单调递增.同时可知f(x1)>f(0)=0,f(x2) (至此,利用隐零点求出了函数f(x)的单调区间.下面利用放缩法进行区间卡根,根据零点存在定理说明在区间 (-1,0)和(0,+∞) 上各恰有一个零点.) 当-1 f(x)=ln (1+x)+axe-x 由ln (x+1)-ea<0,得x 所以,当a<-1时,函数f(x)区间 (-1,0)和(0,+∞) 上各恰有一个零点. 综上所述,a的取值范围是(-∞,-1). 解法2:当a≥0时,在区间(0,+∞)上,f(x)=ln (1+x)+axe-x>0,与题意不符.下面只讨论a<0时的情形. (为直观起见,给出g(x)的图象,如图6所示.) 图6 (为直观起见,给出g(x),f(x)的图象,如图7.) 下面找点说明f(x) 在区间 (-1,0),(0,+∞) 上有零点. 由ln (1+x)-ae=0,解得x=eea-1.所以可得 f(eae-1) 所以f(x) 在区间 (-1,0),(0,+∞) 上各恰有一个零点. 综上所述,a的取值范围是(-∞,-1). 点评:解法1和解法2的基本思路一样,都是按照一定的标准对参数a进行分类讨论,然后借助隐零点将函数的定义域分成若干个单调区间,最后在每个单调区间上卡根,根据零点存在定理说明函数零点的情况. 解法2在求导后将导函数等价变形,使再求导后只需解一个不含参的二次不等式,简化了运算. 解题一般是按照由易到难的顺序进行思考,即先观察、猜想,再分析、思辨,最后论证、求解.题目越复杂越要注意细节,细节往往是打通解题思路的关键. 2.2.1 解题思路二的形成 函数零点的问题往往可以转化为两个函数图象交点问题,因此该题可以考虑参变分离,将函数零点的问题转化为直线与另一个函数图象交点问题,同时还可以避免参数讨论带来的麻烦. 思路二的思维导图,如图8所示. 图8 2.2.2 具体解法 解法3:因为f(0)=0,所以f(x)=0等价于 令g(x)=(x2-1)ln (1+x)+x,则 g′(x)=x[1+2ln (1+x)]. (注意到g(0)=0,所以先讨论g(x)在x>0时的正负情况.) 当x>0时,g′(x)>0,则g(x)单调递增,g(x)>g(0)=0,从而当x>0时,F′(x)>0,F(x)在(0,+∞)单调递增. 由导数定义,得 =1. (为直观起见,下面给出F(x)的图象.) 图9 如图9所示,要使直线y=a与F(x)图象在y轴右侧恰有一个交点,则必然有-a>1,即a<-1. (为直观起见,给出g(x),F(x)的图象,如图10.) 综上所述,当a<-1时,f(x)在区间(-1,0),(0,+∞)各恰有一个零点. 点评:解法3的好处在于对F(x)求导后避免了参数的讨论;难点在于当x趋于0时F(x)的极限值不易求出,虽然可用洛必达法则,但是超出了高中所学.该解法绕开了洛必达法则,利用导数的定义求出F(x)在x=0处的极限,比较巧妙,不易想到. 下面给出两道高考真题,供读者练习. 试题1(2017年全国Ⅰ卷理科)已知函数f(x)=ae2x+(a-2)ex-x. (1)讨论f(x)的单调性; (2)若f(x)有两个零点,求a的取值范围. 试题2(2018年全国Ⅱ卷理科)已知函数f(x)=ex-ax2. (1)若a=1,证明:当x≥0时,f(x)≥1; (2)若f(x)在(0,+∞)只有一个零点,求a. 函数零点问题是高考的常考内容,数形并用、合理分类是解题的关键.区间探点是一个难点,常常可以用放缩法解决.上述方法都是解决此类问题的典型方法,由于方法3中的极限值不易求出,考试中绝大多数考生选择了方法1和方法2. 该题对学生的逻辑推理能力和运算能力要求较高,解题时要求学生注意细节、大胆猜想、合理分类、准确计算,这样才能将问题顺利解决.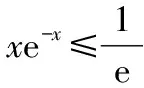
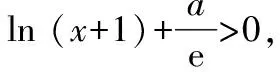
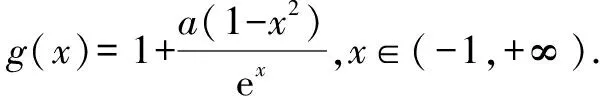
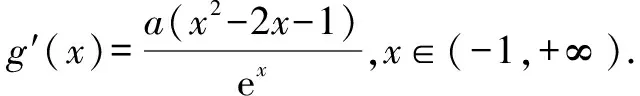
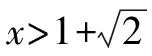
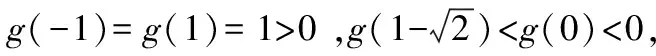
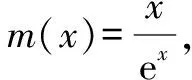
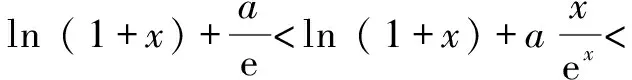
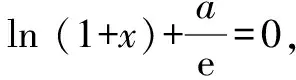
2.2 思路二及解法
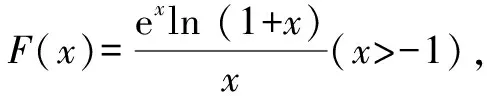
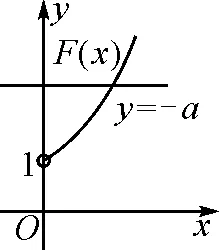
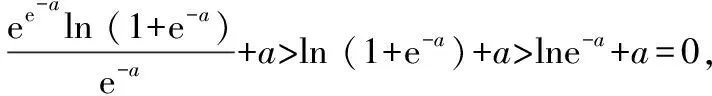
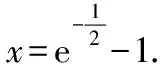
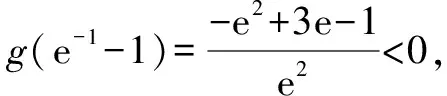

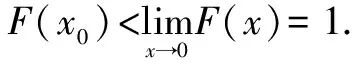

3 试题链接
4 总结
