⦿山东省博兴县第三中学 王丽慧

指数式与对数式综合的不等式恒成立或不等式证明问题，是各类模拟考试及高考的常见题型.解答此类问题的常用策略是利用指数式与对数式的变换关系，构造相同的函数模型，并利用函数的性质求解.下面针对这一方法的应用引例说明.

1 题目呈现

例1已知函数f(x)=x2e3x.

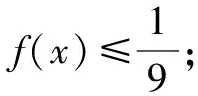
(2)若x>0时，恒有f(x)≥(a+3)x+2lnx+1，求实数a的范围.

本题第(1)问较为基础，直接利用导数求函数的最值即可.第(2)问由不等式恒成立求参数的范围，题目所给的不等式既含有指数式，又含有对数式，可利用“同构法”处理.下面详细阐述同构法的变形与应用技巧.

2 解法综述

在此类问题中常涉及如下几种函数模型：

这些函数的性质直接利用导数即可判断，在此不再赘述.

同构法的应用有两种变换方式：

一种是化指数式，如

另一种是化对数式，如

切线放缩法主要有两个切线模型，即ex≥x+1(x=0时取等号)和x-1≥lnx(x=1时取等号).这两个不等式也可利用导数法直接证明，过程略.

3 问题解答

下面采用两种同构变形方式处理.

3.1 “化指”

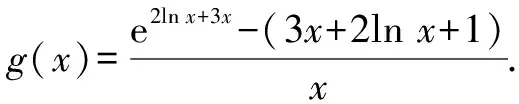
由切线不等式ex≥x+1，得e2ln x+3x≥2lnx+3x+1，当2lnx+3x=0时等号成立.

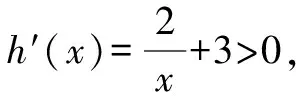
所以

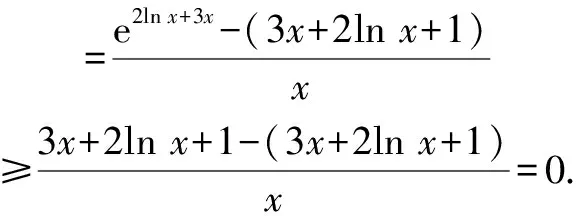
即函数g(x)的最小值为0.

所以满足条件的a的范围是(-∞,0).

3.2 “化对”

由切线不等式x-1≥lnx(x=1时取等号)，得ln(x2e3x)+1≤x2e3x，当x2e3x=1时等号成立.

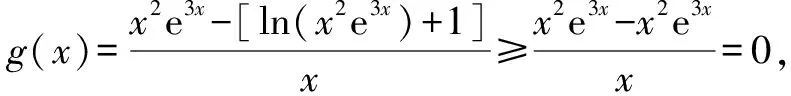
所以满足条件的a的范围是(-∞,0).

4 小试牛刀

例2对于任意x>0，不等式2ae2x-lnx+lna≥0恒成立，则实数a的最小值为______.

解法1:“化指”.

将不等式2ae2x-lnx+lna≥0变形，得2ae2x≥lnx-lna.

因为2ae2x=eln(2a)e2x=eln a+2x+ln 2，所以e2x+ln a+ln 2≥lnx-lna，进一步构造得

e2x+ln a+ln 2+2x+lna+ln 2≥lnx-lna+(2x+lna+ln 2).

化简得

e2x+ln a+ln 2+2x+lna+ln 2≥ln(2x)+2x.

因为2x=eln(2x)，所以

e2x+ln a+ln 2+2x+lna+ln 2≥eln (2x)+ln (2x).

①

设g(x)=ex+x，则式①为g(2x+lna+ln 2)≥g[ln(2x)].又g(x)=ex+x在(0,+∞)内单调递增，所以2x+lna+ln 2≥ln(2x)，即lna≥lnx-2x.

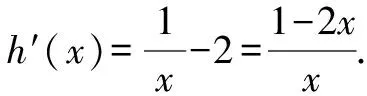
解法2:“化对”.

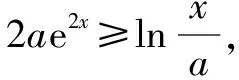
②

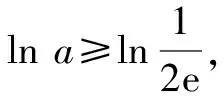
5 考题链接

例3已知函数f(x)=aex-1-lnx+lna.

(1)当a=e时，求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围.

本题是2020年新高考山东卷导数压轴题，所给关系式中既有指数式，也有对数式，可利用同构法处理.下面仅对第(2)问进行解答.

解法1:“化指”.

将不等式aex-1-lnx+lna≥1变形，得aex-1≥lnx-lna+1，即

eln aex-1=eln a+x-1≥lnx-lna+1.

进一步变形得

eln a+x-1+(lna+x-1)≥lnx-lna+1+(lna+x-1)，即eln a+x-1+(lna+x-1)>lnx+x，即

eln a+x-1+(lna+x-1)≥eln x+lnx.

③

设g(x)=ex+x，则不等式③等价于

g(lna+x-1)≥g(lnx).

又g(x)为增函数，所以lna+x-1≥lnx，即

lnx-x+1≤lna.

所以lna≥0,解得a≥1.故a∈[1,+∞).

解法2：“化对”.

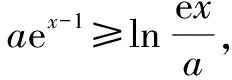
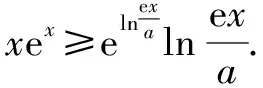
④

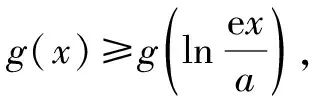
所以lna≥0，解得a≥1.故a∈[1,+∞)

总之，有关指数式与对数式的不等式问题，虽然综合性强，但只要我们掌握相应的处理策略及变形技巧，即可化难为易.