三角形综合问题一题多解
2022-12-19湖北省黄冈市团风中学林菊芳
⦿湖北省黄冈市团风中学 林菊芳
1 引言
从近几年的高考试题来看,解三角形问题成为高考的高频考点.主要考查运用正、余弦定理及其他相关的变形公式解决与三角形有关的证明、求面积、判定三角形形状等问题;题型多样,既有填空题、选择题,也有简答题和综合应用题,侧重考查计算能力和分析问题、解决实际问题的能力[1].下面是笔者总结的几种解题的方法与技巧,供大家参考.
2 三角形证明题“两要”法
三角形中的证明类问题,其基本思路和方法与证明三角恒等式类似.证明的要领可归纳为“两要”:一要“转化”,变陌生为熟悉,就是运用正、余弦定理使原来混合的边、角关系统一为边的关系或角的关系,将其转化为我们熟悉的三角恒等式类的证明问题,或将其转化为代数恒等式类的证明问题;二要灵活运用三角形中的相关结论(公式、定理),例如
sin(B+C)=sinA,cos(B+C)=-cosA,
例1在△ABC中,已知acosA=bcosB,求证:△ABC为等腰三角形或直角三角形.
证法1:从角入手进行证明.
在△ABC中,由acosA=bcosB,得2RsinA·cosA=2RsinBcosB,即sin 2A=sin 2B.
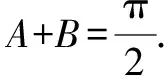
所以,△ABC为等腰三角形或直角三角形.
证法2:从边入手进行证明.
在△ABC中,由acosA=bcosB,得
整理,得c2(a2-b2)=a4-b4.
即c2(a2-b2)=(a2-b2)(a2+b2).
于是 (a2-b2)[c2-(a2+b2)]=0.
所以a=b,或c2=a2+b2.
故△ABC为等腰三角形或直角三角形.
例2在△ABC中,求证:sin2A+sin2B-sin2C=2sinAsinBcosC.
证法1:因为
sin2A+sin2B-sin2C
=cos2(A+B)-cos(A+B)cos(A-B)
=cos(A+B)[cos(A+B)-cos(A-B)]
=-cosC(-2sinAsinB)=2sinAsinBcosC,
所以,原等式得证.
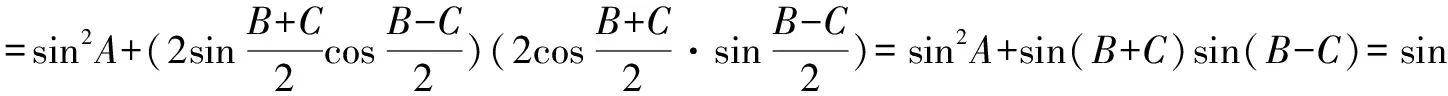
所以,原等式得证.
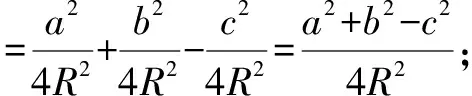
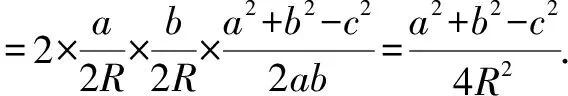
所以,左边=右边,故原等式得证.
3 运用“转化法”判断三角形的形状
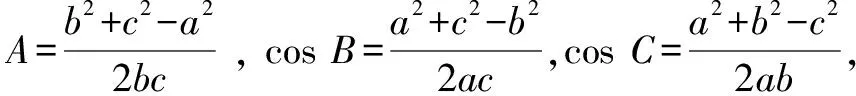
例3在△ABC中,若B=60°,2b=a+c,试判断△ABC的形状.
解法1:由正弦定理,得2sinB=sinA+sinC.
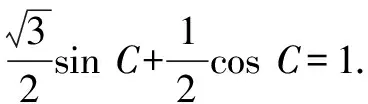
即sin(C+30°)=1.
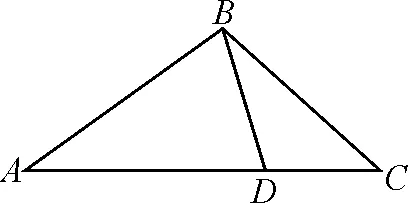
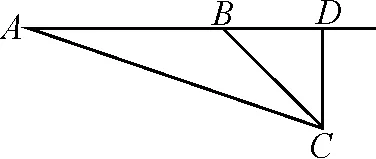
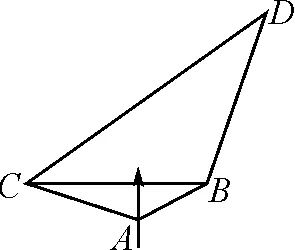
因为0° 于是A=60°=B=C. 故△ABC为正三角形. 解法2:由余弦定理,得b2=a2+c2-2accosB. 整理,得(a-c)2=0,即a=c,从而a=b=c. 故△ABC为正三角形. 例4在△ABC中,已知b2sin2C+c2sin2B=2bccosBcosC,试判定△ABC的形状. 8R2sin2Bsin2C=8R2sinBsinCcosBcosC. 因为sinBsinC≠0,所以sinBsinC=cosBcosC. 于是cos(B+C)=0,则B+C=90°,所以A=90°. 故△ABC为直角三角形. 解法2:将已知等式变为 b2(1-cos2C)+c2(1-cos2B)=2bccosBcosC. 化简得b2+c2=a2. 故△ABC为直角三角形. 其次,针对不同的题型和具体要求,灵活地选用或变形使用三角形面积公式. 例5在△ABC中,已知A=120°,AB=5,BC=7,求△ABC的面积. 图1 图2 例6某职业中专校园背后有一块形似三角形的学农基地(如图2),AB边长为20 m,由点C看AB的张角为40°,在AC上的另一点D处看AB的张角为60°,已知AD=2DC.试求这块学农基地的面积(精确到0.1 m2). 解:依题意可知∠BCA=40°,∠BDA=60°, 则∠DBC=20°,∠BDC=120°.设DC=x. 在△ABC中,AB=20,利用余弦定理可知 AB2=AC2+BC2-2AC×BC×cosC. 即400=(3x)2+(2.53x)2-2×3×2.53x2cos 40°. 解得x≈10.3,从而AC=30.9,BC≈26.03. 故这块学农基地的面积约为257.4 m2. 求解高度与追击问题,大多要利用正、余弦定理,联系高度、距离所在的某个三角形,弄清方向角、方位角,将有关角的关系进行综合应用,观察和求出所在三角形中的某些边、角,当条件不够时,需要创造和寻找条件[3],将有关条件向该三角形转化,最终化为解三角形的问题. 图3 解:由A=15°,∠DBC=45°,可得∠ACB=30°. 因为CD⊥AD,所以 CD=BCsin∠CBD ≈10 500(1.7-1) =7 350(m). 故山顶的海拔高度为10 000-7 350=2 650 (m). 图4 在△ABC中,∠BAC=45°+75°=120°,则 BC2=AB2+AC2-2AB×AC×cos∠BAC =6. 由正弦定理,得 所以∠ABC=45° ,且BC为东西走向. 由题意可知∠CBD=120°. 在△BCD中,由正弦定理,得 所以∠BCD=30°. 于是∠BDC=30°. 综上所述,解三角形问题的关键是要准确理解三角形中的边角关系,会娴熟地运用相关的公式、定理;对于实际应用题,最好能够运用数形结合思想,通过构图、作辅助线等方法帮助分析、思考问题.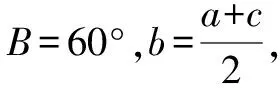
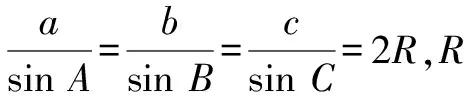
4 巧用公式求三角形的面积.
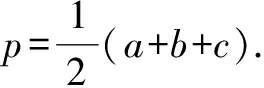
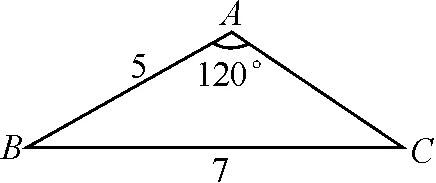
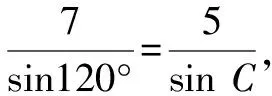
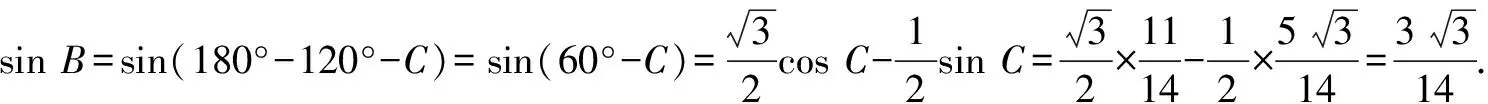
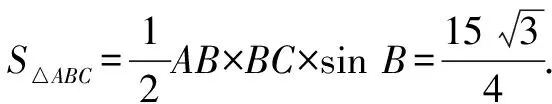
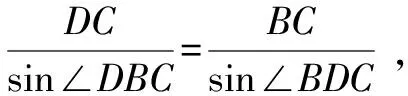
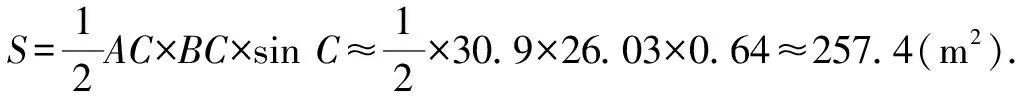
5 活用正、余弦定理求解高度与追击问题
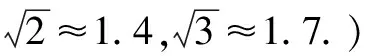
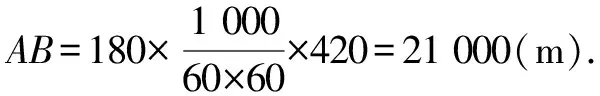
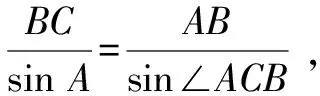
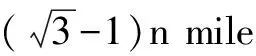
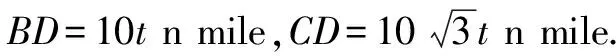
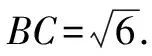

6 结论
