函数与导数问题的转化
——探析2022年浙江高考数学第22题的多种解法
2022-12-19杭州第七中学王浩宇
⦿杭州第七中学 王浩宇
1 试题呈现
(1)求f(x)的单调区间.
(2)已知a,b∈R,曲线f(x)上不同的三点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b).证明:
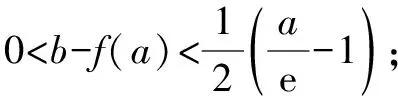
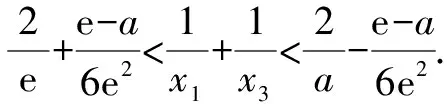
(注:e=2.71828……是自然对数的底数.)
2 思路分析
本题第(1)小题求导即可,较为简单.下面主要对第(2)小题进行思路分析.
2.1 第(2)小题第(ⅰ)问思路分析
分析题干,发现命题者在题干中给出了曲线过点(a,b)的三条切线,题干中的信息可转化为方程b=f′(x)(a-x)+f(x)有三个正根.
思路一:函数零点个数.
由于方程b=f′(x)(a-x)+f(x)无法直接求解,故将其等价转化为函数零点个数问题,画出函数的草图,数形结合分析,可知a,b需满足的条件.此时不等式左侧已经得证,而右侧不等式的证明则可通过分析法,放缩b的范围得证,此为方法1.
思路二:两个函数图象交点个数.
进一步研究发现,可将b单独分离,减少函数中参数的数量,便于计算.将问题转化为两个函数图象交点个数的问题,该方法与方法1类似,在计算上略有简化,此为方法2.
思路三:换元法简化计算过程.
方法2中函数有较多分式,在求导时计算量较大,故对该函数使用换元法(取倒数),将分式转化为整式简化计算,其余做法与方法2类似,此为方法3.
第(ⅰ)问具体思维导图如图1所示.
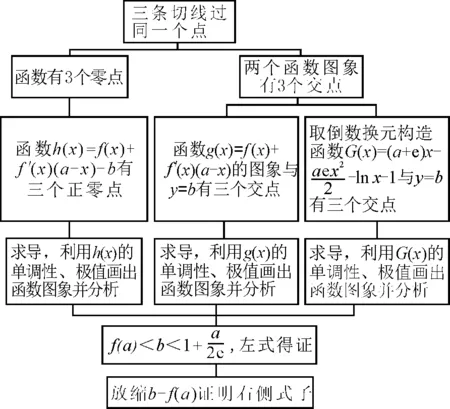
图1
2.2 第(2)小题第(ⅱ)问思路分析
分析题干,由思路分析可知h(x)的单调性,可得条件1.由于所证结论中存在x1,x3,因此大胆进行尝试,写出h(x1)和h(x3)的具体表达式;由于所证结论中未出现参数b,故将h(x1)与h(x3)两式相减消去参数b,可得条件2.此处是该题的一个难点,在没有思路时,可大胆猜测,小心求证.
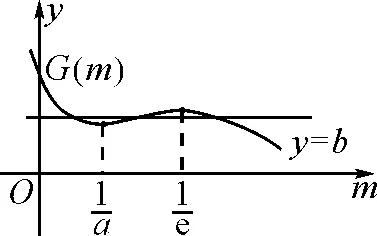
为了缩小已知和求证之间的差距,尝试对所证的结论进行转化.参考a 思路一:单向放缩化简. 思路二:双向放缩化简. 思路三:函数单调性证明. 在方法3构造函数的过程中,发现可以利用函数p(x)的单调性证明,此为方法5.该过程可以避免构造函数和对不等式进行放缩,只需利用p(x)的单调性.在具体计算过程中发现该方法计算量非常大且非常繁琐,构造的函数也较难想到,故并不推荐. 思路四:极限法消参. 对要证结论消参,将x1,x3中的一个用e和a表示,之后证明极端情况成立.所得式子与一元二次不等式有非常类似的结构,故考虑以求解一元二次不等式方式进行证明,该过程需要使用泰勒公式将对数函数进行转化,此为方法6. 第(ⅱ)问思维导图如图2所示: 图2 分析题干: f(x)上不同的三点处的切线为 y=f′(xi)(x-xi)+f(xi)(i=1,2,3) 由于点(a,b)满足上面三个方程,因此b=f′(x)·(a-x)+f(x)有三个正实根x1,x2,x3. 方法1:函数的零点个数. 构造函数h(x)=f(x)-b-f′(x)(x-a),要满足题目条件,需要h(x)有三个正零点.画出h(x)的草图,如图3所示. 图3 方法2:两个函数图象的交点. 设g(x)=f(x)+f′(x)(a-x),则g(x)的图象与y=b有三个交点.g(x)草图,如图4所示. 图4 方法2是方法1的变式,计算量与方法1接近,分别从两函数图象的交点和函数的零点角度分析问题.但以上两种解法均有分式出现,可否一开始就进行换元达到化简运算的目的?由此得出方法3,主要考查学生直观想象的数学核心素养. 图5 方法3:换元法化简计算. 方法1:不等式转化与放缩. 条件1:若0 代入t1+t3的值并化简, ① 方法1最后的求导计算量非常大,主要考查学生数学运算的核心素养.在该方法的研究过程中,因为q(x)的式子结构较为复杂,考虑到x=1既是q(x)的零点,也是q(x)的拐点,故大胆尝试将n-1看成一个整体对q(n)进行化简,构建高阶无穷小量,该方法能够大幅度减少运算量,但是较难想到.虽然该方法的思路高于学生现有的认知,但是教师可以将此作为学生思维的最近发展区,引导成绩优秀的学生进行研究. 方法2:双向放缩不等式. 笔者尝试对方法2中的计算步骤进行化简,尽可能构建已知和未知的相同部分,最终得到更简单的方法3.教师在讲解的过程中,也要做到“优术”,层层递进简化计算. 方法3:对比消元. 和第(ⅰ)问一样,由于证明过程中需要多次用到换元法化简,故笔者尝试在证明开始就使用换元法,得到方法4.方法4的证明思路与方法1类似. 方法4:倒数换元. 放缩不等式除了求导、舍去较小值以外,还能利用函数单调性,方法4就是利用特殊函数p(t)的单调性解决问题.该方法思维含量较少,但是计算量非常大,会消耗学生大量时间,不划算. 方法5:特殊函数法. 笔者继续寻找计算量更小的方法,通过对p(t)的分析,发现p(t)非常接近二次不等式,仅多出一个对数结构的式子.回顾高中数学知识,泰勒公式展开能将对数转化为整式,故尝试使用泰勒公式展开化简问题,方法如下. 方法6:泰勒公式展开. 2022年的浙江高考数学压轴题继承了浙江卷命题简捷明了的风格,并未出现大段文字,为了与明年的全国卷衔接,压轴题还出现了需要转换的内容,学生需要将“三条切线过同一个点”这个条件进行转化,以此获得解题所需的不等式. 该题为双变量含参不等式的证明,属于难题,主要难点在计算和等价转化上.该题不仅考查学生对数学解题“术”的应用,还考查学生对数学解题“道”的理解.对于这类含有参数的不等式,通过构造不同函数,利用函数图象不断等价转化,类比讨论,采用极端位置分析等方法,考查学生数学建模、数学运算、直观想象、逻辑推理等数学核心素养. 解题过程中的感悟如下: 多参函数设主元,整体代换简运算; 泰勒展开来帮忙,适当放缩繁变简.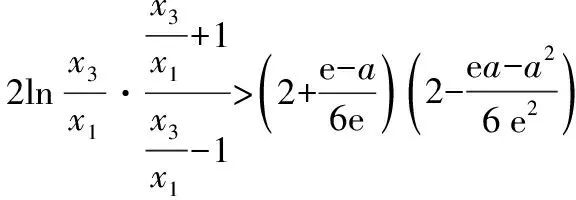
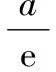

3 具体解答方法
3.1 第(1)小题解答方法
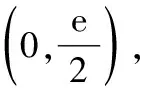
3.2 第(2)小题第(ⅰ)问的解答方法
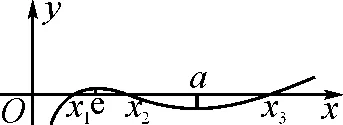
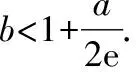

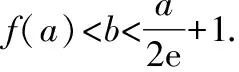
3.3 第(2)小题第(ⅱ)问的解答方法
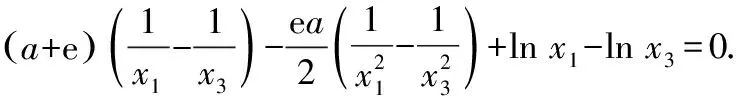

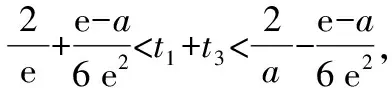
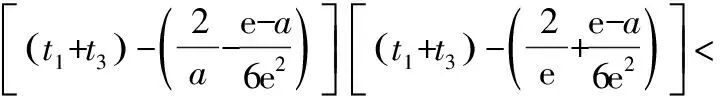
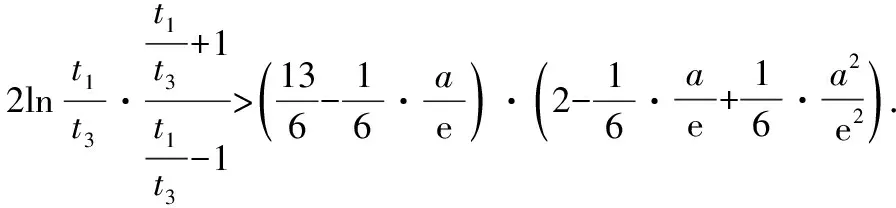
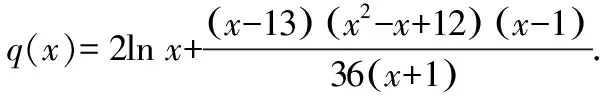

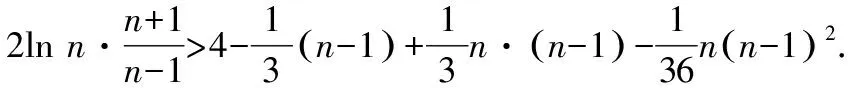
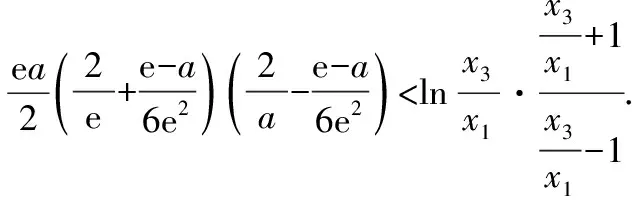


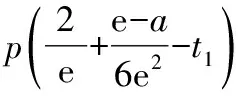
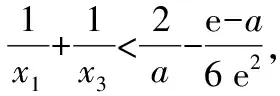
4 总结
