广东省中山市溪角初级中学(528471)谢卫华

1 课前准备,相关历史素材介绍

1.1 古巴比伦泥版上的三角形分割问题

在古代两河流域,中位线知识来源于现实生活中的土地或财产分割.古巴比伦时期的数学泥版MLC1950(图1)上载有以下问题:三角形的高为50,用平行于底边的直线将其分割成高分别为30 和20 的小三角形和梯形,小梯形的面积为320,求原来的三角形以及分割得到的小三角形的底边.这其实是现代的“平行线分线段成比例定理”的应用,用中位线来分割三角形,不过是其中特殊的问题而已.

而在同时期的数学泥版YBC4608(图2)上,记载着六兄弟分割三角形土地的问题,三角形的面积和高已知,三角形是用平行于底边且间距相等的直线来分割的.古人已经知道,分割三角形的这些平行线段的长度是按照等差数列递增的.三角形中位线等于底边的一半,这一性质已经为古人所熟知.

图1

图2

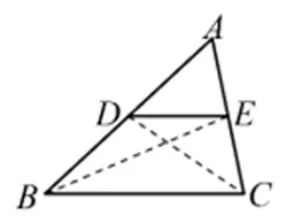
图3

1.2 《几何原本》中的有关命题

公元前3 世纪,古希腊数学家欧几里得在《几何原本》中并没有直接讨论中位线的性质,但卷六给出了更一般的命题(命题VⅠ.2):“将三角形两腰分割成成比例的线段,则分点连线段平行于三角形的底边.”欧几里得证明该定理的方法是:将线段之间的关系转化为三角形面积之间的关系,再将三角形面积之间的关系转化为直线的位置关系.这种方法同样适用于三角形中位线定理.如图3,在ΔABC中,AD=DB,AE=EC.连结BE和DC,因AD=DB,AE=EC,故SΔEAD=SΔEDB,SΔEAD=SΔCED.于是得SΔCED=SΔEDB,故知DE//BC.另一方面,因为SΔEBC=SΔABE=2SΔBDE,而ΔEBC和ΔBDE是等高的,所以BC=2DE.

1.3 刘徽对三角形面积公式的推导

中国汉代数学典籍《九章算术》方田章载有如下问题:“今有圭田广十步,正从二十一步.问:为田几何? ”“又有圭田广五步二分步之一,从八步三分步之二.问:为田几何? ”书中给出的三角形面积公式是:“术曰:半广以乘正从.”这里,“广”就是三角形的底边,“正从”就是三角形的高.术文说的就是:三角形的面积等于底边的一半乘以高.

图4

图5

刘徽(3 世纪)注释说:“半广知,以盈补虚为直田也.亦可半正从以乘广.按半广乘从,以取中平之数,故广从相乘为积步.”这里,刘徽是通过割补的方法来推导三角形面积公式的:取三角形两腰的中点,过中点作底边的垂线,将垂线外侧的小三角形补到上方的相应位置(图4),得到一个矩形,该矩形的面积等于原来的三角形的面积,它的长等于原三角形的高,它的宽等于原三角形底边的一半,即三角形面积等于半底乘以高.刘徽的第二种方法是:连结两腰中点(中位线),过顶点作中位线的垂线,将中位线上方的小三角形分割成两个小直角三角形,分别将它们补到相应位置(图5),得到一个矩形,矩形的长为原三角形的底边长,宽为原三角形高的一半,故三角形的面积等于底乘以半高.

从三角形面积公式的推导过程可以看出,中国古代数学家知道中位线与底边的位置关系和大小关系.事实上,在图5中,将中位线上方的两个小直角三角形分别补到相应位置时,所得到的四边形是矩形(因为一组对边平行且相等),故中位线与底边平行,且等于底边之半.

设计意图通过相关历史知识的介绍,让学生感知中位线定理的历史文化内涵.同时提前掌握一些知识为本节课作铺垫.由于这个知识内容比较多,对于学生来说也有一定的难度,所以把知识的阅读放在课前,给学生充足的时间,让学生思考、消化.

2 教学目标的设定

(1)使学生理解三角形中位线的概念,经历三角形中位线概念形成和性质发现的过程.明确三角形中位线与三角形中线的不同.

(2)使学生掌握三角形中位线定理.在经历探索三角形中位线定理的过程中,学会辅助线的添加方法,同时体会转化的数学思想.

(3)使学生会用三角形中位线定理进行有关的证明和计算,培养和发展学生的创造性思维能力和逻辑推理论证的表达能力.

(4)通过相关知识的介绍,感知数学定理的历史文化内涵.同时体验知识来源于实践、应用于生活.

3 改编历史问题,引出中位线概念

在一块由考古学家发现的古巴比伦泥版记载着这样一个有趣的故事:在巴比伦两河流域,有四位兄弟本来相安无事的生活着,直到一天他们父亲的去世打破了这一平静,大家为了分割父亲留下的一块土地而争论不休,谁都不肯吃亏.土地为三角形形状,请同学们利用所学的数学知识设计方法帮助这四位兄弟解决矛盾,回归平静的生活,同时也要对自己设计的方法有所说明,来说服四兄弟停止争论.

学生活动学生思考,动手操作,比较容易得出图6、图7两种情况.在老师的追问下也一定会出现图8 的情况.

图6

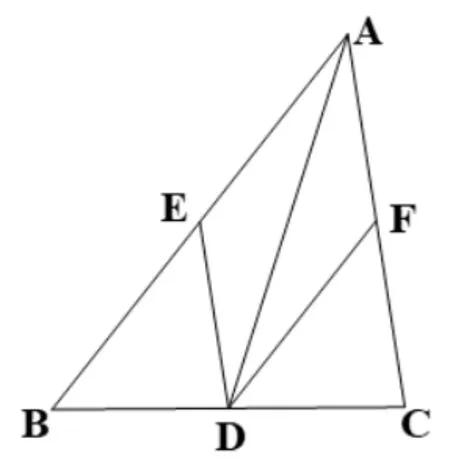
图7

图8

设计意图让学生感知“三角形中线均分三角形面积”这一性质在解决实际问题中的作用,感知数学来源于生活,为中位线概念的引出和区分中线和中位线作铺垫.

当学生无法用逻辑推理的方法证明图8 中4 个三角形面积相等时,老师追问还可以用什么方法来说明?

学生:度量法、叠合法.(此时可让学生动手操作来验证)

师:让我们再来观察第三种设计方案,DE这条线段实质是连结三角形两边中点的线段,我们把这样的线段称为三角形的中位线.它也是三角形中重要的线段,也是我们今天所学的主要内容.

从而引出三角形中位线的定义:连接三角形两边中点的线段.

提出思考一个三角形有几条中位线? 三角形中位线与中线有什么区别?

三角形有三条中位线.

不同点:中线是顶点到对边中点的线段;中位线是相邻两边中点构成的线段.

共同点:它们都是一条线段,分别有三条.

师:上面我们是经过度量、叠合得出图8 中四个三角形的面积相等的.实际测量和叠合法也是研究数学问题的一种方法,而且有理论依据,是可行的,但操作和测量毕竟会产生一定的误差,所以还是要通过严密的逻辑论证来进行证明.

4 探索新知,大胆猜想

拿出叠合法验证时剪下的4 个三角形纸片,让学生拼图得到一个平行四边形,引导学生相互讨论,发现DE与BC的数量和位置关系.

得出猜想:DE//BC,DE=BC.(学生口述,教师板书)

引导学生用语言描述,得出三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

设计意图培养学生观察、猜想及语言表达能力.

5 合作交流,证明新定理

思考如何证明这个猜想?

已知:ΔABC中,D、E分别是AB、AC的中点(如图9).

求证:DE//BC,DE=

从拼图可得证明方法1:延长DE至F,使DE=EF,连结CF,用边角边公理证得ΔADE∽=ΔCFE,可推出AD//CF,AD=FC.又AD=DB,推出DB//FC,DB=FC.推出四边形DBCF是平行四边形.推出DF//BC,DF=BC,又DE=EF,推出DE//BC,DE=

巡堂观察看学生中有没有不同的证明方法,如果有就展示,没有就引导学生思考:利用平行四边形的判定和性质得出第二(图10-1)、第三种(图10-2)证明方法.

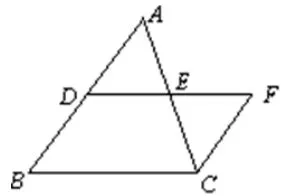
图9

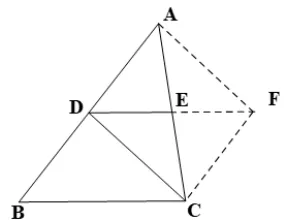
图10-1

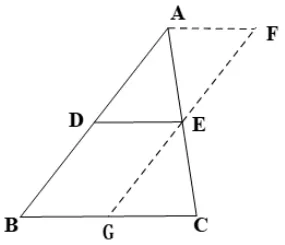
图10-2

师:课前我们学习了三角形中位线有关的历史知识,你们能有什么启发,能想到不同的证明方法吗? 从刘徽得出三角形面积公式中,学生不难得出第4 种(图11)证明方法.

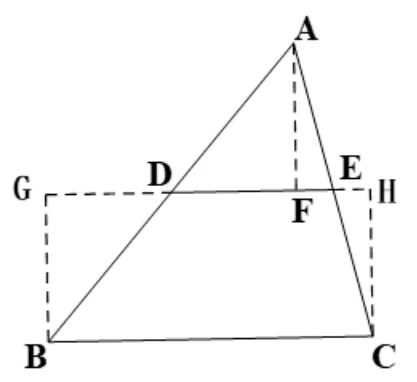
图11

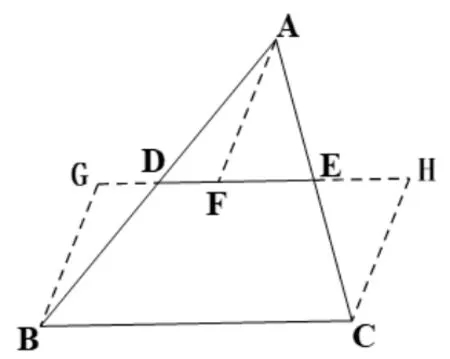
图12

师:如果点F是线段上任意一点,能得出相应的结论吗?

设计意图证明方法的拓展有利于发散学生的思维,也能让学生深刻理解到三角形问题与平行四边形问题中相互的转化思想.

方法点拨:

要证明一条线段的长等于另一条线段长度的一半,方法通常有两种:

(1)将较短的线段延长一倍;

(2)截取较长线段的一半进行转化.

要证明两线段平行,方法通常有两种:利用三线八角或者平行四边形.

设计意图方法的总结有利于学生形成自己的经验.

6 知识运用,形成经验

图13

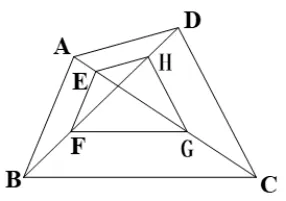
图14

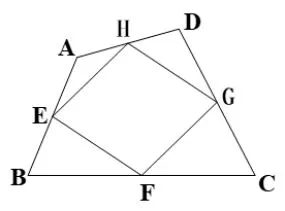
图15

(1)如图13,已知D、E、F分别是ΔABC的三边的中点,试说明:SΔAEF=SΔEBD=SΔDFE=SΔFDC.

(2)如图14,四边形ABCD中,对角线AC与BD相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,四边形EFGH的周长是26cm,则四边形EFGH的周长是____.

(3)如图15,在四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,求证:四边形EFGH是平行四边形.

设计意图第1 题重回引例让学生体会到数学知识的发展起源于人们在现实生活中的实际需求,从得到的新知识解决之前无法解决的问题让学生获得成功感.再增加2 道题让学生形成解决问题的经验.

7 知识小结,经验提升

通过今天的学习你对三角形的中位线是否有了深刻的认识,能谈谈你的想法吗?

要解决几何问题,要审好题,明白什么是已知条件,什么是要求的,能联系到已学什么知识.

今天所学:中点+中点=联想中位线,中点+一半=联想中位线;证明一条线段是另一条线段两倍时辅助线的作法.

8 布置作业,巩固经验

课本第50 页的第5 题.

自己查找有关三角形中位线定理证明的历史资料.

设计意图知识的小结、作业的布置有利于经验的提升与巩固.相关历史资料的查找有利于学生了解到更多历史文化,从而实现数学课的德育价值.

9 教学设计的思考

没有学生参与的教学活动是低效的教学活动.为了调动学生学习的积极性和主动性,本节课结合八年级学生具有好奇、好动的年龄特点.融入数学史从解决历史问题分田地引入,第一时间吸引学生的注意力,激发学生的好奇心和求知欲.本节课改变了以往只重视定理的运用的作法.本节课重点在于中位线定理的探索和证明.设计四兄弟分田地,让学生在解决问题情境中发现中位线,在度量、叠合、拼图中猜想得出中位线定理.从拼图和历史阅读材料中得到证明的思路.证明方法的拓展,解题方法的总结,开阔了学生的视野,积累了经验.也让学生体会到了从特殊到一般的研究方法和三角形、四边形之间进行转化的转化思想.数学史融入课堂能激发学生学习的兴趣,能为新课提供知识的铺垫,也能让学生感受到数学家们为了追求知识的不懈努力和奉献精神,从而激发学生热爱科学,敢于创新的精神,增强学生学习的信心和自豪感.对于八年级的学生来说,对相关的数学史阅读起来还是有一定的困难,因此本节课的设计是,课前给学生阅读三个有关中位线的数学历史,课后安排学生查找三角形中位线证明的有关方法,这样设计可以减轻学生课堂上阅读的困难,也能给足够的时间让学生思考、消化.