SUN Xue-chun,YE Guo-ju,LIU Wei,ZHAO Da-fang

(1.College of Science,Hohai University,Nanjing 210098,China)

(2.School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China)

Abstract:In this paper,we are concerned with a kind of problem of deviation in the process of Analytic Network Process that there is a row or column with a zero vector in the decision matrix.A method to this question is got by improving the super-matrix.Furthermore,we obtain the optimization ranking vector of criterions through calculation and then give a case application.The results enrich and extend the theory of Analytic Network Process.

Keywords:ANP;the super-matrix;relative priority

1 Introduction

Analytic network process(ANP)was put forward by Saaty[1]in order to solve Multiple Criteria Decision Making(MCDM)problems.From then on,there are a large number of literatures concerning the theory and application of the ANP.In[2],the author developed a classification of methods based on criteria interaction phenomenon and discussed the Decision-Making Trial and Evaluation Laboratory Model(DEMATEL)and ANP hybridization which was one of the most promising approaches to handle criteria interactions in a Multiple-Attribute Decision Making.In[3],the author applied a model by combining the graph-theory based on DEMATEL method with an ANP to solve performance evaluation problems for hot spring hotels.In[4],the author suggested an improved information system(IS)project by using ANP and a zero-one goal programming model to solve information system project selection problems.In[5],the author proposed an application of the ANP for the selection of product mix for efficiency manufacturing in a semiconductor fabricator and generated a performance ranking of product mixes.Results of the study provided guidance for orders considering all aspects of the product.In[6],The author processed parametric study and performance-based multi-criteria optimization of the indirect-expansion solar-assisted heat pump through the integration of ANP decision-making with multi-objective particle swarm optimization(MOPSO)algorithm.

Since a lot of subjective information may skew the final result.In order to get a better result,many studies have made some improvements on the ANP method[7–12].One of those,the super-matrix improvements of the ANP have been developed for getting more scientific outcome in[7],Wang studied several main structures of ANP super-matrices.In[8],He Chunchun and Wang researched on ANP form the perspective of algorithm improvements and model combinations.But a row or column in a super-matrix is not noticed as a zero vector.Therefore,in this study,the problem that risk indicators cannot be ranked is solved from the perspective of matrix.

As a common method based on multi-objective decision analysis,ANP aims to compare and sort evaluation criteria by establishing pair comparison matrices among criteria,so as to make the optimal choice.In other words,the higher the relative weight,the larger proportion of the evaluation criterion,and the more attention should be paid to it.However,there may be some deviations in the traditional ANP method,which makes it impossible to sort the evaluation criteria.A row or column in a super-matrix is not noticed as a zero vector.Therefore,in this study,the problem that risk indicators can not be ranked is solved from the perspective of matrix.The improvement of ANP super-matrix is helpful to correct this deviation.Therefore,we transform the judgment matrix and get the relative impact ranking of the evaluation criterion.

The purpose of this paper is to address a particular situation in which risk indicators cannot be ranked,we make some improvements to ANP.The rest of the paper is set out as follows.In Section 2,we present the basics of the ANP.In Section 3,we investigate the existence of a row or column of zero in a super-matrix.Constructing the super-matrix is the core of ANP,when the super-matrix satisfies Theorem 2.5.1,the weight of risk indicators can be obtained through calculation.But it cannot be used in a specific instance when a row or column in a super-matrix is a zero vector.In response to this situation,we apply a method to improve the super-matrix on the basis of ANP as shown in Step 4.Section 4 gives an example.

2 The Basics of ANP Method

2.1 Network Construction

In the ANP method,the decision problem is formulated into a network structure.A general structure of ANP is shown in Figure 1.

Figure 1:General structure of ANP

ANP divides system elements into two major parts:control layer and network layer.The elements of these two parts relate to each other.As shown in Figure 1,the direction of the arrows in the network structure plays an important role of representing the right relationship between two parts[8].

The control layer includes the goal of the evaluation program and decision criteria.All decision criteria are considered independent of each other and governed only by objective factors.The control layer can have no decision criteria,but at least one goal should be presented.The network layer is composed of factors that is dominated by the control layer.As shown in Figure 1,risk factor groups{R1,R2,R3,···,Rn},and there are risk indicators under each risk indicator group,for example:factor groupRiincludes risk factors{ei1,ei2,···,eini},an arc with an arrow represents an inner dependence relation in a cluster and an arrow represents a dependence among clusters and factors across different clusters.And there is a case where there is no connection between the elements of two sets.

2.2 Pair-Wise Comparisons

After determining the network structure,pair-wise comparisons between different clusters and facts are given by the risk assessment experts.The comparison of dominance is as follows:give a criterion and compare the importance of two elements under this criterion.A scale of 1-9 is used to indicate how important the two elements relative to the criterion.The 1-9 scale is displayed in Table 1.

Table 1 1-9 scale[13]

Experts put forward the degree of influence that each criterioneif(f=1,2,···,ni)toepq(p,q=1,2,···,ni),which was denoted byaif,using the 1-9 scale.Then the normalized vector is derived though

Therefore pair-wise comparisons are expressed in Table 2.

Table 2 pair-wise comparison of risk factors[7]

2.3 The Establishment of the Super-Matrix

After passing the consistency test,the normalized eigenvectors of each pair-wise comparison matrix can be combined into a super-matrix.LetWijbe the influence degree of indicator setRion indicator setRj.

Due to the number of risk fact sets in the network layer aren,so the number ofWijisn×n.If the indexenihas no influence on the indexenj,the corresponding element inWijis 0.LetWijbe a element of the super-matrixW:

In the super-matrixW,eachWijis a matrix whose column is normalized or equal to 0.But the super-matrixWis not a column normalized matrix.

2.4 Constructing of the Weighted Super-Matrix

In order to let the super-matrix be a column normalized matrix,we need to construct the weighted matrix.Rise the pair-wise comparison between factors to the pair-wise comparison between factor groups{Ri}(i=1,2,3,···,n).Let control layer elementsPas guidelines to search the influence degree of the factor groups{Ri}.In a similar way,if the factor groupRihas no influence on factor groupRj(j=1,2,3,···,n),the corresponding element in normalized vector is 0.Experts are asked to reach the degree of direct influence that each indicatorRjexerts on each indicatorRi,which is denoted bybmi(m=1,2,3,···,n),using the 1-9 scale.A normalized vector is then derived byand shown in Table 3.

Table 3 pair-wise comparison of risk groups

So,all normalized vectors form the weighted matrixU:

Finally,the weighted super-matrixW*is obtained by combining the super-matrixWand the weighted matrixU:W*=U⊙W,(⊙:w*=uijWij)[7].

2.5 Determination of Indexed Weight

After getting the weighted super-matrix,we can not determine the weight.The weighted super-matrixW*needs a stable tackle thatW*is constantly multiplied and normalized to form matrix convergence.

Theorem 2.5.1[7]If the weighted super-matrixW*satisfies

(1)the maximum eigenvalue ofW*is 1;

(2)the maximum eigenvalue 1 is a single;

(3)modulus of other eigenvalues are all less than 1.

Then,

(i)there is the limited matrix ofW*,letW∞=limn→∞(W*)n;

(ii)each column ofW∞is identical and is the normalized eigenvector ofW*belonging to the maximum eigenvalue 1;

(iii)the weighted of indexed is obtained,each column ofW∞is the relative weighted of indexes.

3 A New Approach to Improve the Weighted Hyper-Matrix of ANP Method

3.1 The Problem Formulation

In the process of solving the weighted super-matrix,there might be a situation:there is no influence between factor groupRiand factor groupRj,as in this case,the weighted super-matrixW*must be a column(or a row)where all elements of them are zero.It can be seen that the magnitude of all eigenvalue ofW*is less than 1 and 1 is not eigenvalue ofW*.In this study,we will solve the problem that risk indicators cannot be ranked from the perspective of matrix.

3.2 The Methods for the Improved ANP

In this case,if there is a column(or a row)where all of them are zero in the weighted super-matrixW*.On the basis of the obtained weighted super-matrix,we improve it for further calculation.Thus,we can get improved calculation steps of the weighted supermatrix of ANP method:

Step 1 According to Section 2.2,the pair-wise comparisons by decision-makers are obtained.

Step 2 According to Section 2.3,based on Step 1,the super-matrix is obtained.

Step 3 According to Section 2.4,we compute the weighted super-matrixW*.

Step 4 We improve the weighted super-matrixW*.

∃j,∀i(i=1,···,n),defining the column(or the row)of the weighted supermatrixW*are.nis the size of the weighted super-matrixW*.

Step 5 By calculating the dominance degree of risk indicators,risk indicators are sorted by the dominance degree.

This approach is based directly on conventional operation of ANP.It is shown that the use of known methods may lead to nothing when using the basic ANP method.It is seen that our method provides a feasible solution under the premise of ensuring the subjectivity of decision makers.The main advantage of the proposed method is that it provides a simple way of solving about a complex situation.

Using numerical examples,it is shown that the proposed improved ANP method may provide the final ranking of risk indicators.

4 Case Study

The objective of this case is to solve the complex decision problem by using ANP with LPT(live,play,transportation).We attempt to develop an ANP model about the travel problem.Now,we have four destinations:Chengdu,Gansu,Sanya,Xinjiang.The first includes a control hierarchy or network of criteria that control the interactions:liveP1,playP2,transportationP3.The second consists of three kinds of subnetworks:benefitsR1,costsR2,risksR3.So,ANP with LPT model about travel problem is shown in figure 2.

figure 2:the ANP structure of the play place

Two types of connections between nodes contained in groups are represented infigure 2 as one-way influence and two-way influence.If there is one-way influence between the two groups are represented with directed arrows.The two-way influence is represented by bi-directed arrows.GroupR1includes two risk factors:convenienceR11and experienceR12.GroupR2includes two risk factors:trafficR21and residenceR22.And groupR3includes two risk factors:epidemicR31and surroundingsR32.

Step 1The pair-wise comparisons by the decision-maker are shown in Table 4 and Table 5.

Table 4 pair-wise comparison of R1j(j=1,2)to R11

Table 5 pair-wise comparison of R1j(j=1,2)to R12

We can obtain the comparison matrixw11for the factors inR1to the factors inR1through Table 4 and Table 5.

In the similar way,

Step 2According to step 1 result,the super-matrix is

Step 3The decision-maker givesRj(j=1,2,3)to aRi(i=1,2,3)level of direct impact on 1-9 scale.

We can get the weighted matrixUthrough Table 6,Table 7 and Table 8.

Table 6 pair-wise comparison of{Ri}(i=1,2,3)to R1

Table 7 pair-wise comparison of{Ri}(i=1,2,3)to R2

Table 8 pair-wise comparison of{Ri}(i=1,2,3)to R3

Thus,the weighted super-matrixW*:

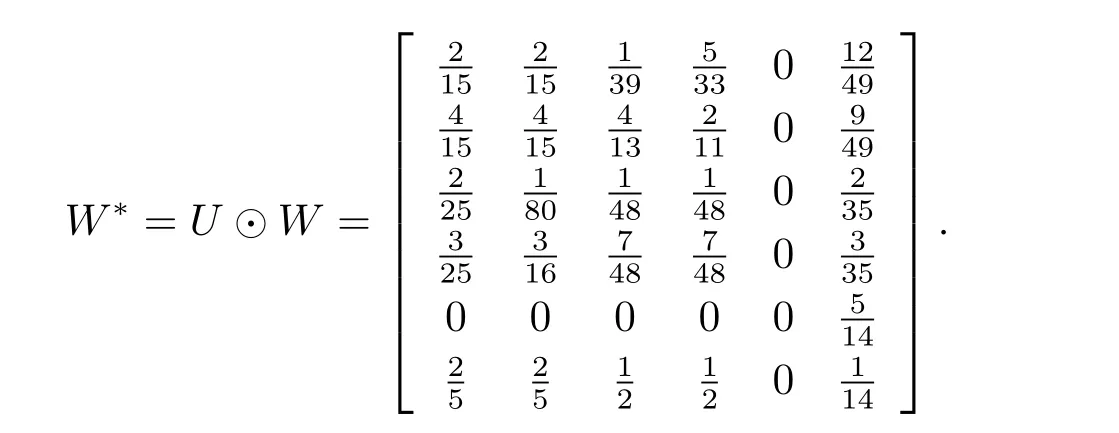
By computation to find the eigenvalue of the weighted super-matrixW*.

It can be found that the six output eigenvalues are all less than 1,and 1 is not the eigenvalue of the weighted super-matrixW*.

Step 4We improve the weighted super-matrixW*,as follows:

The eigenvaluesEand corresponding eigenvectorsVof the improved super-matrix can be obtained by calculation.

Step 5It can be obtained that the maximum eigenvalue ofW*is 1,and the only normalized eigenvector that corresponds to 1 is

Now,Let us do a consistency check.According to the mean random consistency index(RI)of order 1-15 in table 9,we can obtain that the consistency test for the super-matrix

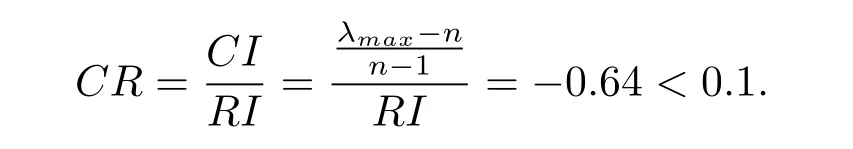
Therefore,we consider the consistency of the matrix to be acceptable.

Table 9 1-15 order average random consistency indicator(RI)[14]

Based on the results from the only normalized eigenvector,the priority of the risk factors in this case is

Thus,we can solve such situations by the improved Analytic Network Process.

5 Conclusions

In this study,in order to solve the problem that the ANP of risk factors cannot be ranked,the weight of risk factors can be obtained by transforming the weighted super-matrix and then the influence degree of risk factors of policymaker’subjective can be obtained under a certain criterion.A case is used to validate the applicability and efficacy of the proposed approach.The results show that the proposed method can be an effective method for ANP risk ranking.

Although the proposed method is an effective improvement strategy for ANP,it still has some limitations,because calculations against large amounts of data can be relatively cumbersome.