质数、积数及“哥德巴赫猜想”

2022-11-03冯浚

数理化解题研究 2022年30期

关键词：算数哥德巴赫猜想总和

冯浚

(甘肃省兰州市税务局 730070)

在数学领域，对数的基础研究始终都没有停止.对于质数，目前尚无较为简明的类似偶数,奇数的数学表达式.鉴于此，可以从数最初的状态入手，发现新的特性.

1 质数、积数

1.1 定义

1.1.1 质数的定义：正整数中，只能被1和自己整除的数为质数.

为了便于研究，用q表示质数.

故，在正整数中，按由小到大顺序排列的质数是：1,2,3,5,7,11,…，对应表示为：q1,q2,q3,q4,q5,q6,….

1.1.2 积数的定义：正整数中，质数以外的数为积数.同理，用p表示积数.则p=m1×m2.

(1)

p称为积数，m1,m2称为因数(m1>1,m2>1)；m1,m2若为质数，则称为质因数；上式中最小的因数一定是质数，可称其为最小质因数.如16=4×4=2×8.

则其因数为4,或2,8；最小因数为2，也为16的最小质因数.

1.2 表达式

1.2.1 积数的表达

根据质数,积数的特性，经逻辑推导，对最小质因数为qn的所有积数及qn，可用下列式子表示：

(2-1)

式(2-1)中，n=0，±1，±2，±3，…， 1≤n2≤(q2-1)，1≤n3≤(q3-1)，…，1≤nn-1≤(qn-1-1).

由于q2=2，q3=3，q4=5，q5=7，q6=11，…，qn,则n2=1，n3=1，2，n4=1，2，3，4，n5=1，2，3，4，5，6，n6=1，2，3，4，5，6，7，8，9，10，…nn-1=1，2，3，…，qn-1-1.

1.2.2 质数的表达

与(2-1)式同理，对1和所有大于qn的质数，以及最小质因数大于qn的所有积数，可用下式表示：

(2-2)

式(2-2)中，n=0,±1,±2,±3,… ，1≤n2≤(q2-1),1≤n3≤(q3-1),…,1≤nn≤(qn-1).

由于：q2=2,q3=3,q4=5,q5=7,q6=11,…,qn,则n2=1，n3=1,2，n4=1,2,3,4，n5=1,2,3,4,5,6，n6=1,2,3,4,5,6,7,8,9,10，…nn=1,2,3,…,qn-1.

1.3 负积数,负质数

根据正,负数的特点，为了便于研究,计算等，引入负积数,负质数概念.

A,则式(2-1)积数的表达为

(2-3)

式(2-3)中，n=0,±1,±2,±3,…，1≤n2≤(q2-1),1≤n3≤(q3-1),…，1≤nn-1≤(qn-1-1).

由于q2=2,q3=3,q4=5,q5=7,q6=11,…,qn,则n2=1，n3=1,2，n4=1,2,3,4，n5=1,2,3,4,5,6，n6=1,2,3,4,5,6,7,8,9,10，…nn-1=1,2,3,…,qn-1-1.

举例如下：

(1)当最小质因数为2时，即qn=q2=2 ，n1=q1-1=1-1=0 ；则：P2=q2!n

n=0,±1,±2,±3,…，

n=0,±1,±2,±3,…，n2=1.

n=0,±1,±2,±3,…，n2=1，n3=1,2.

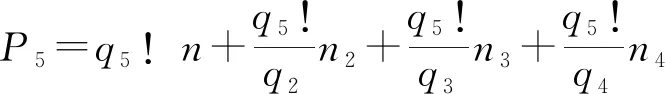
n=0,±1,±2,±3,…，n2=1，n3=1,2，n4=1,2,3,4.

n=0,±1,±2,±3,…，n2=1，n3=1,2，n4=1,2,3,4，n5=1,2,3,4,5,6，B,则式(2-2)质数的表达为

(2-4)

式(2-4)中，n=0,±1,±2,±3,…

1≤n2≤(q2-1),1≤n3≤(q3-1),…,1≤nn≤(qn-1).

由于：q2=2,q3=3,q4=5,q5=7,q6=11,…,qn

则：n2=1，n3=1,2，n4=1,2,3,4，n5=1,2,3,4,5,6，n6=1,2,3,4,5,6,7,8,9,10，…nn=1,2,3,…,qn-1.

举例如下：

n=0,±1,±2,±3,…，n2=1.

n=0,±1,±2,±3,…，n2=1，n3=1,2.

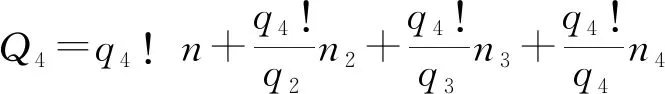
n=0,±1,±2,±3,…，n2=1，n3=1,2，n4=1,2,3,4.

n=0,±1,±2,±3,…，n2=1，n3=1,2，n4=1,2,3,4，

n5=1,2,3,4,5,6.

n=0,±1,±2,±3,…，n2=1，n3=1,2，n4=1,2,3,4，n5=1,2,3,4,5,6，n6=1,2,3,4,5,6,7,8,9,10.

1.4 首数集

1.4.1 积数首数集

分析式(2-3)可得，PN是由若干个等差数列组成.而最小质因数的不同，则等差数列的数量也不相同.

在式(2-3)中，所有大于0并且小于qn!(即：0∠PN∠qn!)的数称之为首数，并且所有的首数组成首数集，用Bn表示.

则式(2-3)可用下式表示：

PN=qn!n+Bn

(3-1)

式(3-1)中，n=0,±1,±2,±3,….

由此可以得出结论一：qn及最小质因数为qn的所有积数，可组成若干个公差为qn!的等差级数.即其可用若干个公差为qn!的等差级数表示.

其中，最小数为qn，次之为(qn)2.

举例如下：

(1)最小质因数由2开始，当最小质因数为2时，qn=q2=2 ，qn!=q2!=1*2=2，n1=q1-1=1-1=0 ；则：B2=0；P2=q2!+B2=1*2n+0=2n.故q2时，q2!=2，B2=0，P2=2n.即偶数表达式P2=2n，可表述为：其为2及最小质因数为2的所有积数.

P3=q3!n+B3=1*2*3*n+3=6n+3故q3时，q3!=6，B3为：3，P3=6n+3

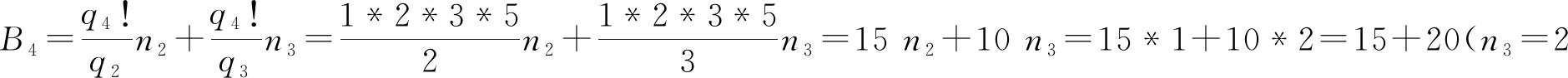
由于q4!为30，即公差为30；故调整后B4为：5,25,故q4时，q4!= 30，B4为：5, 25 (即B4=5,25)

P4=30n+5,30n+25

由于q5!为210，即公差为210；故调整后B4为：203,161,119,77,133,91,49,7，即7,49,77,91,119,133,161,203.故q5时，q5!= 210，B5为：7,49,77,91,119,133,161,203，P5=210n+7,210n+49,210n+77,210n+91,210n+119,210n+133,210n+161,210n+203，即P5=210n+{7,49,77,91,119,133,161,203}.

1.4.2 质数首数集

同理，在式(2-4)中，所有大于0并且小于qn!(即：0∠QN∠qn!)的数称之为首数，并且所有的首数组成首数集，用An表示.

则式(2-4)可用下式表示：

QN=qn!n+An

(3-2)

式(3-2)中，n=0,±1,±2,±3,….

由此可以得出结论二：1和所有大于qn的质数，以及最小质因数大于qn的所有积数，可组成若干个公差为qn!的等差级数.即其可用若干个公差为qn!的等差级数表示.

其中，最小数为1，次之为qn+1；最小积数p为(qn+1)2.

举例如下：

(1)当q2时，即qn=q2=2时，

对1和所有大于2的质数，以及最小质因数大于2的所有积数如下：

qn=q2=2，qn!=q2!=1*2=2，n2=q2-1=2-1=1；

Q2=q2!n+A2=1*2n+1=2n+1

故q2时，q2!=2，A2=1，Q2=2n+1.

即奇数表达式Q2=2n+1，可表述为：其为1和大于2的所有质数，以及最小质因数大于2的所有积数的总和.

(2)q3时，即qn=q3=3时，

对1和所有大于3的质数，以及最小质因数大于3的所有积数如下：

qn=q3=3，qn!=q3!=1*2*3=6，n2=1，n3=1,2；

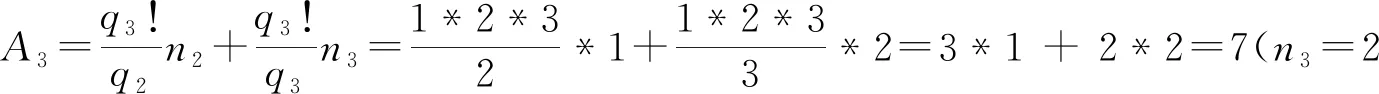
由于q3!为6，即公差为6；故调整后A3为：1, 5；故：q3时，q3!=1*2*3=6，A3为：1, 5(即A3=1, 5)Q3=6n+1,6n+5

(3)q4时，即qn=q4=5时，对1和所有大于5的质数，以及最小质因数大于5的所有积数如下：

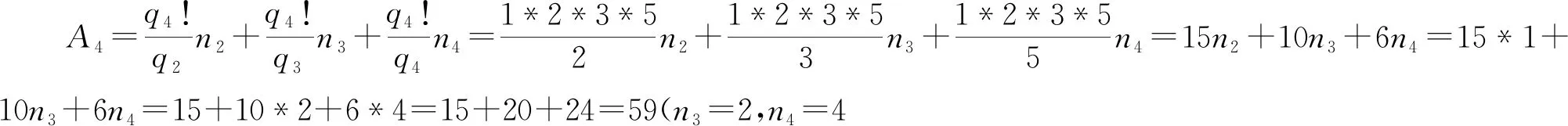
及：15+10*2+6*3

=53(n3=2,n4=3时)

=47(n3=2,n4=3时)

=41(n3=2,n4=1时)

=49(n3=1,n4=4时)

=43(n3=1,n4=3时)

=37(n3=1,n4=2时)

=31(n3=1,n4=1时)

由于q4!为30，即公差为30；

故调整后A4为：1,7,11,13,17,19,23,29

故：q4时，q4！=1*2*3*5=30，

A4为：1,7,11,13,17,19,23,29

Q4=30n+1,30n+7,30n+11,30n+13,30n+17,30n+19,30n+23,30n+29

即Q4=30n+{1,7,11,13,17,19,23,29}

(4)q5时，即qn=q5=7时，

对1和所有大于7的质数，以及最小质因数大于7的所有积数如下：

qn=q5=7，qn!=q5！=1*2*3*5*7=210，

n2=1，n3=1,2，n4=1,2,3,4，n5=1,2,3,4,5,6；

=105n2+70n3+42n4+30n5=105*1+70*2+42*4+30*6=105+140+168+180

=593(n3=2,n4=4,n5=6时)

及.….…(分别带入具体数值，此处略)

由于q5!为210，即公差为210；

故调整后A5为1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.

故q5时，q5！=1*2*3*5*7=210，

A5为：1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.

Q5=q5！n+A5=210n+{1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.}

1.4.3 质数首数集与积数首数集之间的逻辑关系

在QN中，对于An，其开始连续qn+1级的等差数列，为An+1和Bn+1.

举例如下：

q3时，即qn=q3=3，qn+1=q4=5，q3!=6；B3为：3；P3=6n+3；A3为：1,5；

Q3=6n+1,6n+5

A3开始连续q4级(即5级)的等差数列具体为：

1,7,11,13,19,25

5,11,17,23,25,29，

则A4为：1,7,11,13,17,19,23,29；

B4为：5,25.

2 质数、积数的有关特性和规律

之前，对于质数做了基本的分类.即：在正整数中，按由小到大顺序排列的质数是：1,2,3,5,7,11,…，对应表示为：q1,q2,q3,q4,q5,q6,…qn….

将具体相关数值带入各表达式中，分析研究可初步得到一些规律和特性，即积数表达式与质数表达式的逻辑关系等等.特别是首数集非常重要，其为质数,积数的重要基础和内容，其特性和规律在某种意义上也是质数,积数的特性和规律.

在此，可将质数等做进一步分类.

2.1 初步分类及基本特性

2.1.1 常质数：数值1存在于任意An中，可将1称为常质数.

2.1.2 基楚质数：分析表达式(3-2)等，可将q1,q2,q3,q4,q5,q6,…qn称为基楚质数.

并且，通过已知的基楚质数，应用式(3-2)等可以求出更大更多的基楚质数.

结论三：通过已得出的基楚质数，可求出小于任意一个数的所有质数.即：可以求出任意大的所有质数.

2.1.3 对称分布情况：

(1),Pn,Bn,Qn,An相对于0对称分布.

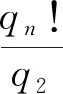
2.2 质数,积数的有关特性和规律

2.2.1 以上表达式带入具体数值后如下：

(1)q1时，即qn=q1=1时，为常质数.Pn及Qn相同，为：n.

(2)q2时，即qn=q2=2时，q2!=2，

B2为0，P2=2n；其为偶数表达式.

A2为1，Q2=2n+1；其为奇数表达式.

则此时，基楚质数为2，

(3)q3时，即qn=q3=3时，q3!=6，B3为：3，

P3=6n+3

A3为1,5

Q3=6n+1,6n+5

具体为1,7,11,13,19,25,︱31,…6n+1

5,11,17,23,25,29,︱35,…6n+5

则此时，基楚质数为2,3，

(4)q4时，即qn=q4=5时，q4!=30，B4为：5,25

P4=30n+5,30n+25

具体为5,35,65,95,125,…30n+5

25,55,85,115,145,…30n+25

A4为：1,7,11,13,17,19,23,29

Q4=30n+{1,7,11,13,17,19,23,29}

具体为：

则此时，基楚质数为2,3,5，(qn+1)2=(q5)2=49

故：7,11,13,17,19,23,29,31,37,41,43,47均为质数(结论二).

(5)q5时，即qn=q5=7时，q5!=210，

B5为：7,49,77,91,119,133,161,203，

P5=210n+{7,49,77,91,119,133,161,203}

具体为：

A5为：1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.

Q5=q5！n+A5=210n+{1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,121,127,131,137,139,143,149,151,157,163,167,169,173,179,181,187,191,193,197,199,209.}

具体为：

则此时，基楚质数为2,3,5,7，(qn+1)2=(q6)2=121

故：11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113均为质数(结论二).

2.2.2 有关特性和规律

(1)在QN中，设任意一个数Qm；则Qm=qn!nm+Am,若Qm为因数是qm的积数，则Qm一定能被qm整除；并且，在QN中，存在Qm+n，nm+n=(nm+nn).即Qm+n=qn!nm+n+Am=qn!(nm+nn)+Am=qn!nm+Am+qn!nn

当nn是qm的倍数时，Qm+n也一定是因数为qm的积数.

结论四：在QN中，对于任意一个因数为qm的积数Qm，在其所在的等差数列中，相对于Qm其等差数是其qm的整数倍时，其一定是因数为qm的积数，并且只有其是因数为qm的积数.当qm为qn+1时，其一定是最小质因数为qn+1的积数.

由于在QN中，所有积数的最小质因数是qn+1，故：在QN中，任一公差为qn！的等差数列，在连续qn+1项中只有一个最小质因数为qn+1的积数.

(2),对于QN，可进一步分为QN+1和PN+1.

即：对1和所有大于qn的质数，以及最小质因数大于qn的所有积数，可进一步分为：1和所有大于qn+1的质数，以及最小质因数大于qn+1的所有积数，即：QN+1；和最小质因数为qn+1的所有积数(含qn+1)，及PN+1.即：QN=QN+1+PN+1

(3),在QN中，最小质因数为qn+1的所有积数在QN中占比最大，占QN全体的qn+1分之一；所占比例递减的积数分别是最小质因数为qn+2,qn+3,qn+4,…的积数.

并且，在QN中，

…

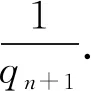
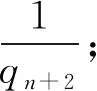
结论五：qn越大，其积数在QN中所占比例越小.

3 关于“哥德巴赫猜想”

哥德巴赫1742年给欧拉的信中哥德巴赫提出了以下猜想:任一大于2的偶数都可写成两个质数之和.但是一直无法证明.

现就质数,积数和偶数等进一步分析研究如下.

3.1 偶数与两个质数之差

由以上可得：

3.1.1 在QN中，对于任意两个数Ax,Ay；此两数之差为Xn，在其所在的等差数列中，此两数同时加,减相同数量的公差，其相对应的两数之差均满足此条件，即两数之差同样为Xn；所以在QN中有无数组数满足此条件.

即Xn=Ax-Ay=qn!nAx-qn!nAy

举例如下：

(1),q3时，即qn=q3=3时，q3!=6，基楚质数为2,3；

B3为：3，P3=6n+3

A3为：1,5

Q3=6n+1,6n+5

具体为：1,7,11,13,19,25,︱31,…6n+1

5,11,17,23,25,29,︱35,…6n+5

设：Ax=23，Ay=7；

则：X3=23-7=16

X3=16=qn!nAx-qn!nAy=n6*23-n6*7

即：Q3中，17-1,及23-13,35-19,41-25…均为16.

(2)q4时，即qn=q4=5时，q4!=30，基楚质数为2,3,5，

B4为：5,25

P4=30n+5,30n+25

A4为：1,7,11,13,17,19,23,29

Q4=30n+{1,7,11,13,17,19,23,29}

具体为：

设Ax=23，Ay=11；

则X4=23-11=12

X4=12=qn!nAx-qn!nAy=n30*23-n30*11

即Q4中，23-11,53-41,83-71,113-101…均为12.

3.1.2 在QN中，对于任意两个数Ax,Ay；此两数之差为Xn，在其同时连续qn+1级的等差数列中，其相对应的在QN+1中，有(qn+1-2)组满足此条件，另外2组分别是：Ax为最小质因数是qn+1的积数和Ay为最小质因数是qn+1的积数的一组.

举例如下：

q3时，即qn=q3=3时，q3!=6，基楚质数为2,3；qn+1=q4=5；B3为：3，P3=6n+3

A3为：1,5

Q3=6n+1,6n+5

设：Ax=23，Ay=7；

则：X3=23-7=16

X3=16=qn!nAx-qn!nAy=n6*23-n6*7

即：Q3中，其同时连续5级的等差数列为：(23,7),(29,13),(35,19),(41,25),(47,31).

其相对应的在Q4中，有3组满足此条件，分别是(23,7),(29,13),(47,31).另外两组不在Q4中的是Ax为最小质因数是5的积数，即积数为35的一组(35,19)和Ay最小质因数是5的积数，即积数为25的一组(41,25).

3.1.3 在QN中，对于任意两个数Ax,Ay；此两数之差为Xn.

(1),当QN大于等于Q2时，由于其中所有的数均为奇数，故Xn一定是偶数.

(2),当：q3时，即qn=q3=3时，q3!=6，基楚质数为2,3；B3为：3，P3=6n+3

A3为：1,5

Q3=6n+1,6n+5

具体为：1,7,11,13,19,25,︱31,…6n+1

5,11,17,23,25,29,︱35,…6n+5

在Q3中，对于任意两个数Ax,Ay；此两数之差为偶数X3，在其同时连续q4级(即5级)的等差数列中，对于Ax-Ay(即X3大于0小于等于6，即0

满足X3为2的有5组.

即X3=Ax-Ay=2时，有5组，

如(5,7),(11,13),(17,19),(23,25),(29,31)；

满足X3为4的有5组.

即X3=Ax-Ay=4时，有5组，

如(1,5),(7,11),(13,17),(19,23),(25,29)；

满足X3为6的有10组.

即X3=Ax-Ay=6时，有10组，

如(1,7),(7,13),(13,19),(19,25),(25,31),(5,11),(11,17),(17,23),(23,29),(29,35)；

对于Ax-Ay(即X3)大于6，即6

由于任意一个大于6的偶数，均可用：6n+2,6n+4,6n，这三种情况之一表示；

故在Q3中，对于两个数Ax,Ay；此两数之差可为任意一个偶数X3，同理，在其同时连续q4级(即5级)的等差数列中，至少有5组满足此条件.当X3为6n+2或6n+4时，有5组；当X3为6n时，有10组.

例如：满足X3为8的有5组.

即X3=Ax-Ay=8=6+2时，有5组，

为(5,13),(11,19),(17,25),(23,31),(29,37)；

满足X3为10的有5组.

即X3=Ax-Ay=10=6+4时，有5组，

为(1,11),(7,17),(13,23),(19,29),(25,35)；

满足X3为12的有10组.

即X3=Ax-Ay=12=6+6=2*6时，有10组，

为(1,13),(7,19),(13,25),(19,31),(25,37),(5,17),(11,23),(17,29),(23,35),(29,41)；

(3),q4时，即qn=q4=5时，q4!=30，基楚质数为2,3,5，

B4为：5,25；P4=30n+5,30n+25

A4为：1,7,11,13,17,19,23,29

Q4=30n+{1,7,11,13,17,19,23,29}

由于在Q3中，对于任意两个数Ax,Ay；此两数之差X3可以是任意一个偶数.同时，由于在Q3中，在其同时连续q4级(即5级)的等差数列中，其相对应的在Q4中，至少有3组满足此条件.

故在Q4中，对于两个数Ax,Ay；此两数之差同样可以是任意一个偶数.同时，在其同时连续q5级(即7级)的等差数列中，至少有7组满足此条件.其相对应的在Q5中，至少有5组满足此条件.

以此类推，可以得出结论六：在QN中，对于两个数Ax,Ay；此两数之差Xn可以是任意一个偶数.即：对于任意一个偶数，可以由无数组QN中的两数之差表示.

3.1.4 对于任意一个偶数，在QN中，有无数组两个数之差满足此条件(结论六).而QN越大，

在QN中，质数占比越小(结论五).则在QN中无数组两个数之差满足此条件的，并且同为质数的比例越大.

所以可以得出结论七：对于任意一个偶数，可以由无数组两个质数相减表示.

3.2 偶数与两个质数之和

3.2.1 在QN及An中，质数和积数的有关情况一

(1)对于Qx，Ax的前qx+1项的总和为Ax+1+Bx+1.

例如，对于Q5，A5的前q6项的总和为A6+B6.

(2)对于Qx中，所有积数的最小质因数为qx+1.

…

举例如下：

对于Q5中，所有积数的最小质因数为q6.

…

(3)在Qx中，由于在以上积数占比的计算中都包含最小质因数，并且各积数均大于或等于其最小质因数的平方.所以，在Qx中，Ax的前qx+1项的总和中，同一最小质因数的积数在其中的实际占比小于或等于其算数平均占比.

对于Qx，在Ax的前qx+1项的总和中，

…

3.2.2 在QN及An中，质数和积数的有关情况二

(1)对于式(3-2)，即QN=qn!n+An；具体为：Q3=q3!n+A3，即Q3=6n+A3

Q4=q4!n+A4，即Q4=30n+A4

Q5=q5!n+A5，即Q5=210n+A5

Q6=q6!n+A6，即Q6=2310n+A6

Q7=q7!n+A7，即Q7=30030n+A7

Q8=q8!n+A8，即Q8=510510n+A8

对于式(3-1)，即PN=qn!n+Bn；具体为：P3=q3!n+B3，即P3=6n+B3

P4=q4!n+B4，即P5=30n+B4

P5=q5!n+B5，即P5=210n+B5

P6=q6!n+B6，即P6=2310n+B6

P7=q7!n+B7，即P7=30030n+B7

P8=q8!n+B8，即P8=510510n+B8

…

(2)按照以上算式进行计算得出如下：

对于Q3，Q3=q3!n+A3，即Q3=6n+A3；在A3的前q4项的总和中，积数只有最小质因数为q4的积数.其占比用Z3表示为：0.2.

对于Q4，Q4=q4!n+A4，即Q4=30n+A4；在A4的前q5项的总和中，积数为最小质因数为q5到q7的积数.积数算数平均占比(总和)用Z4表示约为：0.23836.

对于Q5，Q4=q5!n+A5，即Q5=210n+A5；在A5的前q6项的总和中，积数为最小质因数为q6到q16的积数.积数算数平均占比(总和)用Z5表示约为：0.27186.

对于Q6，Q6=q6!n+A6，即Q6=2310n+A6；在A6的前q7项的总和中，积数为最小质因数为q7到q41的积数.积数算数平均占比(总和)用Z6表示约为：0.25060.

对于Q7，Q7=q7!n+A7，即Q7=30030n+A7；在A7的前q8项的总和中，积数为最小质因数为q8到q128的积数.积数算数平均占比(总和)用Z7表示约为：0.24440.

对于Qn，在An的前qn+1项的总和中，积数算数平均占比(总和)用Zn表示；若以Y轴为Zn，X轴为Qn，则其关系如下：

由此具体分析如下：

对于Q3和Q4，其属于开始阶段，在Ax的前qx+1项的总和中，由于部分因素未出现，其不能完全吻合总体特性和规律.但自Q5后，各种因素的出现，故其可显示总体特性和规律.即：对于Qx，在Ax的前qx+1项的总和中，所有积数算数平均占比(总和)在出现峰值0.27186后，其趋势为逐渐缓慢下降.

并且，由此可得推断一：对于Qx，在Ax的前qx+1项的总和中，所有积数算数平均占比(总和)均处于较低的占比，且远低于50%.

3.2.3 证明

由结论七可得：任意一偶数Xn，则在QN中，存在Ax,Ay，满足：Xn=Ax-Ay(0

当qn！

对于Xn,Ax,Ay，也满足：Xn=(Ax-mqn-1！)-(Ay-mqn-1！)；(m=1,2,3,…)

当m1qn-1！开始大于Ay起，(Ay-m1qn-1！)<0，此时，Xn实际为两数相加.并且自此起到(m2+1)qn-1！开始大于Ax起的前1级，即0<(Ax-m2qn-1！),{Ax-(m2+1)qn-1！}<0时，至少有qn组满足此(由于qn！

例如：Xn=104，则q4！

m1=4,m2=21，

即Xn=(127-4*6)-(23-4*6)=103+1

Xn=(127-5*6)-(23-5*6)=97+7

Xn=(127-6*6)-(23-6*6)=91+13

…

Xn=(127-20*6)-(23-20*6)=7+97

Xn=(127-21*6)-(23-21*6)=1+103 共18组.

(1)当Xn≤q4！，即Xn≤30时，

可代入具体数值计算证明：Xn均可由一组以上两个质数相加表示.

即：Xn=qx+qy

(2)当q4！

存在Xn=(Ax-mq3！)-(Ay-mq3！)=(Ax-m*6)-(Ay-m*6)(m=1,2,3,…)

即Xn=(Ax-m1*6)-(Ay-m1*6)=(Ax-m1*6)+(m1*6-Ay)

Xn={Ax-(m1+1)6}+{(m1+1)6-Ay}

Xn={Ax-(m1+2)6}+{(m1+2)6-Ay}

…

Xn=(Ax-m2*6)+(m2*6-Ay)

满足等式，并且等式右边两数均大于0的至少有q4组，即至少有5组.

而在这些组中，包含q4分之一的为最小质因数是q4的积数；故在这些组中，即：在此至少5组中，包含5分之一的为最小质因数是5的积数；所以在这些组中，至少有3组为：“在A4的前7项的总和”中的数.由于其积数算数平均占比(总和)小于50%(Z4约为：0.23836)；所以其中至少有一组两数均为质数.并且具体计算也可证明.

例如，例如Xn=32，则q4！

也满足：Xn=(Ax-mq3)-(Ay-mq3)=(43-m*6)-(11-m*6)

m1=2,m2=7，

即Xn=(43-2*6)-(11-2*6)=31+1

Xn=(43-3*6)-(11-3*6)=25+7

Xn=(43-4*6)-(11-4*6)=19+13

Xn=(43-5*6)-(11-5*6)=13+19

Xn=(43-6*6)-(11-6*6)=7+25

Xn=(43-7*6)-(11-7*6)=1+31 共6组.

最小质因数是5的积数的组为：(25,7)和(7,25)；在A4的前7项的总和中的数有4组，为(31,1),(19,13),(13,19),(1,31)；并且均为质数.

(3)当q5！

存在Xn=(Ax-mq4！)-(Ay-mq4！)=(Ax-m*30)-(Ay-m*30)(m=1,2,3,…)