黄联辉

(福建省德化第三中学，362500)

一、从初中的视角证明“三点共线”

方法1利用平角的定义证三点共线

例1如图1,在∆ABC中,延长两边的中线BD，CE到点F，G,使DF=BD,EG=CE,求证:G，A，F三点共线.

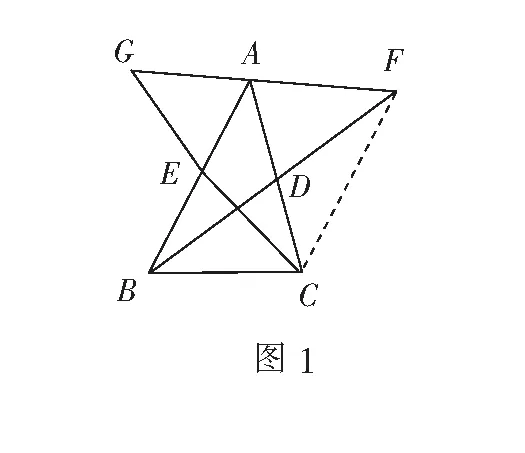
分析要证明G，A，F三点共线,可证明∠FAC+∠BAC+∠GAB=180°.

由于BD=DF,AD=CD,连结CF,则四边形ABCF为平行四边形,AF∥BC,∠FAC=∠ACB.

同理∠GAB=∠ABC.

∴∠FAC+∠BAC+∠GAB=∠ACB+∠ABC+∠BAC=180°.

说明用平角的定义是证明“三点共线”使用频率最高的、最大众、最主流的方法.

方法2先求其中两点所在直线的解析式,再验证第三点也在该直线上,证明三点共线.

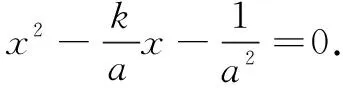
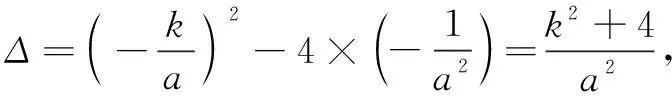
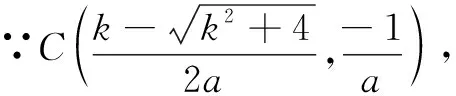
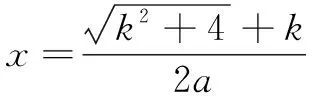
所以,点B在直线CO上,即C，O，B三点共线.

说明此方法比较适用于带参数的函数,但此法对学生运算能力的要求较高,关键是“消参”.

方法3利用“过直线外一点有且仅有1条直线与已知直线平行(或垂直)”证三点共线

例3如图3,在∆ABC中,M为BC的中点,AD为∠BAC的平分线,CD⊥AD于点D,AE是∠BAC的外角∠CAK的平分线,CE⊥AE于点E,CD和CE的延长线分别交射线BA于点H，K.求证:M，D，E三点共线.

证明∵AD为∠BAC的平分线,CD⊥AD.

∴CD=DH.

∵M为BC的中点, ∴DM∥AB,

同理可证DE∥AB,M，D，E三点共线.

说明要证D，E，M三点共线,AD为∠BAC的平分线,CD⊥AD,可证D是CH的中点,M为BC的中点,所以DM∥AB,同理DE∥AB,所以D，E，M三点共线,其依据是“过直线外一点有且仅有1条直线与已知直线平行”这一基本事实.

方法4利用“较短两边之和等于最长边”证三点共线

例4如图4,在等腰∆ABC和等腰∆ADE中,AB=AC,AD=AE,∠BAC=∠DAE,过点A作线段AM⊥DE于点M,连结CM.若BD+DM=CM,求证:C，E，D三点共线.

证明∵∆ADE为等腰三角形,AM⊥DE,DM=ME,

∴AB=AC,AD=AE,∠BAC=∠DAE,∠CAE=∠BAD,

∴∆BAD≌∆CAE,∴BD=CE,

∴BD+DM=CM.

∵CE+DM=CE+ME=CM,

∴C，E，D三点共线.

说明此方法比较适用于研究三条线段之间的大小关系的题型.

方法5用“同一法”证三点共线

例如图5,⊙O1与⊙O2相交于A，B两点,公切线切两圆于C，D两点,M为CD的中点,求证:A，B，M三点共线.

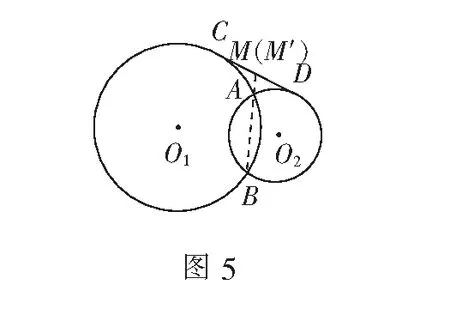
分析可连结AB并延长交CD于M′,再利用切割线定理证明M′与M重合,则点M在AB的延长线上,即A，B，M三点共线.

证明连结BA,并延长交CD于点M′.

∵CD是⊙O1与⊙O2的公切线,

∴CM′2=AM′·BM′,M′D2=AM′·BM′.CM′=DM′.

即M′是CD的中点, 又M是CD的中点,

∵M′与M重合,即M在BA延长线上,

∴A，B，M三点共线.

说明同一法最显著的特点是——先假设一个新的点,再证明新的点与原有的点重合(系同一点).

方法6利用“共边同侧等角线”证三点共线

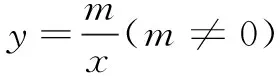
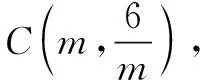
∴tan∠BOM=tan∠DOH,∠BOM=∠DOH,

∴O,B,D三点共线.

说明此方法涉及到角,因此经常借助内(外)角和定理或圆周角定理或三角函数的方法加以证明.

二、从高中的视角证明“三点共线”

方法7利用“点到直线的距离为零”证三点共线

例7平面直角坐标系中,已知点A(-1,0),B(0,1),C(1,2),试证:A，B，C三点共线.

说明此方法要求熟记“点到直线的距离公式”,且通常在已知条件中有出现许多点的坐标.

方法8利用“两直线的夹角为零度”证三点共线

例8平面直角坐标系中,已知点A(-1,0),B(0,1),C(1,2),试证:A，B，C三点共线.

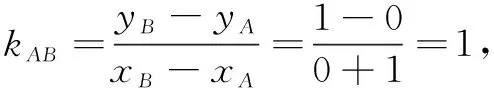
说明“有公共点的两直线夹角为零度时则它们重合”是此证法的依据所在.

方法9利用向量平行的充要条件证三点共线

例9平面直角坐标系中,已知点A(-1,0),B(0,1),C(2,3),试证:A，B，C三点共线.

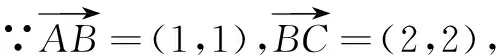
又线段AB和线段BC有公共点B,故有A，B，C三点共线.

说明此法主要是用向量的充要条件加以证明.

方法10用梅涅劳斯定理的逆定理证三点共线

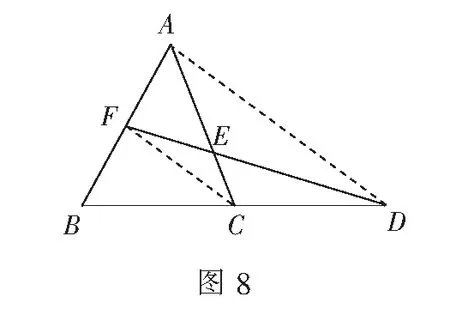
值得一提的是,该方法对于解初中数学的竞赛题较为适用,但中考或其他考试一般较少用得到.

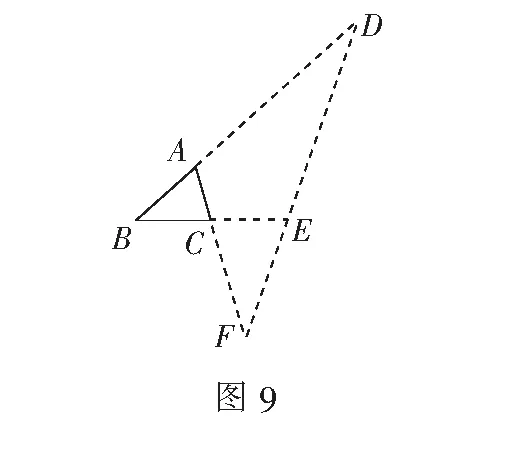
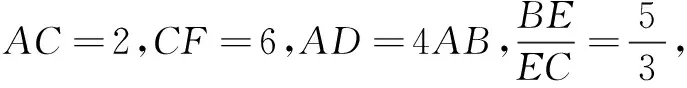
说明该方法对于解初中数学的竞赛题较为适用,一般中考题比较少用.

方法11利用线段的定比分点坐标公式证明三点共线

例11平面直角坐标系中,已知点A(1,2),B(2,4),C(3,6),试证:A，B，C三点共线.

说明运用此证明方法时,务必要牢记线段的定比分点坐标公式,否则不可轻易使用.

值得一提的是,“三点共线”证明并不局限于以上的11种方法,还有许多其他的证法,比如,可以借助四点共圆、借助帕普斯定理、通过证三角形的面积为零等方式证明三点共线,限于篇幅,这里不一一列举．