江苏省金湖县第二中学 (211600) 尤文君

考察近几年高考数学把关题，多以导数为工具来求解函数中的相关问题的，此类试题具有结构独特、技巧性高、综合性强等特点，而通过构造函数是解导数问题的最基本方法，如果能够根据问题特征，挖掘隐含信息，对所给的表达式进行有目的的代数变形，然后以此同构式构造出新函数，再利用此函数的性质求解问题，往往能使复杂题目的解决变成一路坦途．本文以近几年的高考题和模考题为例，对在处理导数问题时使用同构函数法的几个思考途径进行归类和总结，供读者朋友参考．

一、挖掘隐含关系

例1 已知不等式ex-x-1>m[x-ln(x+1)]对一切正数x都成立，求实数m的取值范围．

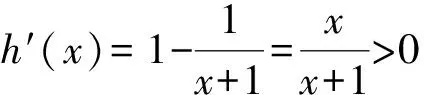
点评：通过所给不等式的分析、变形，挖掘了题设中f(x)>f[ln(x+1)]的隐含关系，通过构造函数f(x)=ex-mx后，条件式就是说明此原题函数是一个单调递增函数，这是成功解题的关键．

二、理顺特殊元素

点评：本题在挖出同构关系中颇费了一番功夫，而对照几个常见的同构式，理顺ex与lnx的关系是重要的思维走向．

三、注重结论分析

例3 已知f(x)=(a+1)lnx+ax2+1，当a≤-2时，求证∀x1,x2∈(0,+∞)，使得|f(x1)-f(x2)|≥4|x1-x2|成立．

点评：通过对所需证明的结论进行分析、变形，找到了要证明题中的结论，即需证明f(x1)+4x1≥f(x2)+4x2，成功地转化了解题方向，分析转化是重要的解题思想．

四、构造相关函数

例4 已知f(x)=xex+1，g(x)=lnx+x+1，(1)求f(x)单调区间；(2)设h(x)=f(x)-kg(x)(k>0)，若h(x)≥0恒成立，求实数k的取值范围．

解析：(1)由f(x)=xex+1，则f′(x)=(x+1)ex+1，当x∈(-∞,-1)时，f′(x)<0，当x∈(-1,+∞)时，f′(x)>0，所以f(x)的单调减区间为(-∞,-1)，增区间为(-1,+∞)．

(2)由h(x)≥0恒成立，即xex+1≥k(lnx+x+1)恒成立，也就是elnx+x+1≥k(lnx+x+1)恒成立．构造函数h(x)=ex-ex，则h′(x)=ex-e，当x≥1时，h′(x)≥0，所以h(x)在[1,+∞)单调递增，于是h(x)≥h(1)=0，所以ex≥ex，当x=1时取等号，所以elnx+x+1≥e(lnx+x+1)，结合所给条件，可得e(lnx+x+1)≥k(lnx+x+1)，当x∈[1,+∞)时，lnx+x+1>0，所以k≤e，当且仅当x=1时取等号，实数k的取值范围是(0,e]．

点评：此题为了顺利求出参数范围，构造了一个与条件相关的函数，通过探求新函数的性质帮助解决问题，此手法在许多不等关系中经常被采用，所起到的效果也是非常好的．

五、及时换元处理

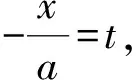
点评：由于待证的不等式比较复杂，在分析、化简、变形的基础上，再经过换元处理，成功找到同构关系，这样问题的解决就是希望在眼前了．

六、利用参数放缩

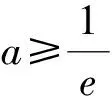
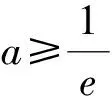
点评：本题中利用给出的条件，及时的将函数式中的参数进行放缩处理，构造了一个新的待证不等关系，优化了问题的结构，为发现同构式、建立新函数解题奠定了坚实基础．

一般来说，同构式需要构造一个母函数，而这个母函数又需要满足指数与对数跨阶，单调性和最值易求等特征，因此常见的同构形式大多以自然对数的底数e的指数函数或对数函数及其同族函数作为母函数，如y=x+lnx，y=xex等．经过同构变形，再结合复合函数的单调性，可以快速解决求参数的取值范围、确定函数值域、证明不等式等问题．