王兴锋，张氢，秦仙蓉，孙远韬

（同济大学机械与能源工程学院，上海 201804）

在钢框架结构的设计中，结构的杆件一般从标准型钢库中选取，通过组合得到满足性能要求的最佳设计方案，因此，钢框架结构的优化设计是一个典型的离散优化问题.

当前对钢框架结构离散优化问题的研究，几乎都侧重于提出新的优化方法，以期获得满足工程精度要求的近似最优解.这些优化方法覆盖了元启发式算法［1-5］、优化准则法［6-7］、基于梯度的数学规划方法［8-9］，但几乎没有研究能够针对特定类型的钢框架结构离散优化问题，明确指出优化方法的求解结果与全局最优解的距离.为确定优化算法的求解精度，一般做法是通过与多种优化方法的结果进行对比.这种论证方法只能粗略地说明优化算法的求解精度，而且需要广泛地、有代表性地选取作为对比的优化算法.为证明某种优化算法的求解精度，一种更直接的方法是，获取优化问题的全局最优解，或者优化问题的理论下限（假设优化问题为最小化问题）.尽管在工程实际问题中，由于约束的复杂性，几乎不可能得到优化问题的全局最优解，但针对特定类型的钢框架结构离散优化问题，还是有可能获得全局最优解或理论下界.

在这方面，已经有少数学者展开了研究.针对含应力和位移约束、以体积最小为目标的钢框架结构离散优化问题，Van 等［10］提出了一种优化方法，通过将原优化问题建模为混合整数优化问题，从而得到离散优化问题的全局最优解.针对含体积约束、以柔度最小为目标的钢框架结构离散拓扑-尺寸优化问题，Kanno［11］提出了一种混合整数二阶锥规划的建模方法，将原优化问题转化为一个凸规划问题，从而也得到了原问题的全局最优.kureta 等［12］针对负泊松比的周期性框架结构的离散优化问题，提出了一种混合整数的线性规划方法.Hirota等［13］将混合整数的线性规划建模方法，进一步推广到具有负热膨胀能力的周期性框架结构的离散拓扑优化中.

在钢框架结构中，杆件的截面参数包括截面宽度、高度、板厚，以及截面面积、强弱轴惯性矩等.对于标准型钢截面，这些截面参数是相互关联的，选定某一个截面参数则意味着同一截面的其他参数也被选中，故称为关联离散变量［14-15］.在以上研究中［10-13］，关联离散变量是通过0-1 变量进行定义，以此来表征是否选择了某个标准截面，对应的优化问题都是含0-1 变量的凸规划问题.对于此类优化问题，一般采用隐枚举法（如分支定界法）进行求解，计算效率非常低，若结构中的杆件数量或可选的标准截面增多，计算效率会大幅下降.

有鉴于此，本文提出了一种新的离散变量处理方法，即基于凸组合的线性松弛方法.该方法将关联离散变量进行线性松弛，从而将结构的刚度矩阵转化为设计变量的线性函数，根据这一优势，可以将钢框架结构离散优化中的多种非线性优化问题进一步建模为凸规划问题.本文重点分析了两类非线性优化问题：柔度约束的最小体积问题和体积约束的最小柔度问题.根据刚度矩阵与设计变量的线性关系，将柔度约束的最小体积问题转化为半定规划问题，将体积约束的最小柔度问题转化为二阶锥规划问题.采用现成的优化求解器，直接求解这两类凸规划问题，快速得到松弛问题的全局最优解，也就是离散优化问题的理论下界.

1 离散变量的定义方法

在钢框架结构的离散优化设计中，杆件截面从标准型钢库中选取：

式中：S为标准截面构成的集合；为标准型钢的截面参数；p为标准型钢的个数.

对于关联离散变量，一种常见的处理方法为采用0-1变量：

式中：ti为0-1 变量，用于表征某一标准截面是否被选中.这种定义方法的本质，是在p维的0-1 离散空间与标准截面集S之间定义了一种映射关系.

若优化数学模型中包含0-1 变量，则求解特别耗时，为此，本文提出了一种新的离散变量定义方法，即基于凸组合的线性松弛方法.

对于平面钢框架结构的优化问题，若只考虑结构的轴向变形和弯曲变形，则结构的刚度矩阵仅仅与杆件的截面面积和惯性矩有关.因此，在作者前期的研究［16］中，提出了以截面面积和惯性矩为设计变量的定义方法：

式中：A、I分别为杆件的截面面积和惯性矩.考虑到标准型钢的A和I是关联离散变量，优化过程中需要同时选取某一标准截面的A和I，故在每一次优化迭代后将设计变量圆整到标准截面.根据式（5），标准型钢可视为二维空间中的一个离散点（见图1）.

图1 基于凸组合的线性松弛Fig.1 Linear relaxation based on convex combination

对于空间中的任意多个点，总是存在一个包含所有点的最小凸多边形（即凸包），使得凸多边形内的任意一点，都可以用凸多边形顶点的凸组合进行描述.因此，提出一种基于凸组合的线性松弛方法，将式（5）表示的变量定义方法推广到连续空间：

在式（6）～（9）中，将基于凸多边形的线性松弛方法应用于二维空间，若将这一方法应用于一维空间时，就退化为一种常见的松弛方法.以桁架结构的离散优化问题为例，假设杆件的可选截面集为：

式中：c1、c2为凸组合系数.显然，式（12）～（14）就是式（6）～（9）的一维形式.

根据式（6）～（9），离散优化问题的设计变量变成连续松弛变量（即凸组合系数），而标准截面的截面面积和惯性矩成为设计变量的线性函数.由此，钢框架结构的刚度矩阵成为凸组合系数的线性函数.根据这一特性，可以将两类典型的钢框架结构离散优化问题，即柔度约束的最小体积问题、体积约束的最小柔度问题，分别转化为松弛的凸规划问题.

2 凸规划建模

2.1 柔度约束的最小体积问题

在钢框架结构的离散优化中，柔度约束的最小体积问题可表达如下：

式中：Li、Ai分别为第i个杆件的长度和截面面积；n为杆件的总数；K为结构的刚度矩阵；U为节点位移列阵；F为载荷列阵；为柔度上限.

根据桁架结构的研究［17-18］，桁架结构的柔度约束和力平衡约束可等效于矩阵的半正定约束：

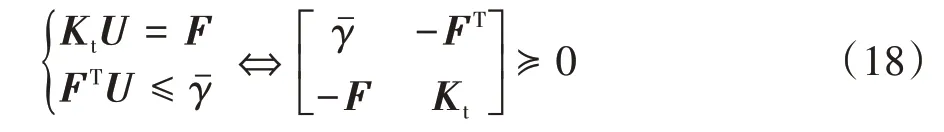
式中：Kt为桁架结构的刚度矩阵.

式（18）成立的一个重要前提条件，就是Kt为杆件截面面积的线性函数.根据本文提出的线性松弛方法，钢框架结构的刚度矩阵也成为设计变量的线性函数，故同样可以将钢框架结构的柔度约束最小体积问题转化为半定规划问题：

式中：K(C)为钢框架结构的刚度矩阵；C为凸组合系数矩阵.

针对半定规划问题，当前已经有多个成熟的优化求解器，如MOSEK［19］、SeDuMi［20］.应用这些求解器，可以快速得到半定规划问题的全局最优解，也就是离散优化问题的理论下界.

2.2 体积约束的最小柔度问题

在钢框架结构的离散优化中，体积约束的最小柔度问题可表达如下：

根据Kanno［11］，体积约束的最小柔度问题可转化为混合整数的二阶锥规划问题：

式中：wil(l=1，2，3)是杆件i的应变余能；sil(l=1，2，3)是杆件i的内力；bil(l=1，2，3)为杆件i的方向列阵，具体计算方法可参照文献［11］的附录A.

其中，Ai、Ii属于关联离散变量，Kanno［11］采用0-1变量的定义方法进行处理.为提高问题的求解效率，快速得到离散优化问题的理论下界，本文采用基于凸组合的线性松弛方法来重新定义离散变量：

式（33）～（36）仅包含线性约束，不改变优化问题的数学特性，故所得到的优化问题仍然属于二阶锥规划问题.二阶锥规划问题可以用成熟的优化求解器（如MOSEK、CPLEX［21］、Gurobi［22］或SeDuMi）进行快速求解，进而得到原离散优化问题的理论下界.

3 数值算例

通过求解一跨四层钢框架结构的离散优化问题，对所提出的方法进行验证.钢框架结构的尺寸、杆件分组和加载情况如图2所示.杆件的弹性模量为2.1×105MPa，体积上限为0.18 m3，柔度上限为25.结构中的杆件从标准规格中的H 型钢［23］中选取（见表1），H型钢在二维空间中的分布如图1所示.

图2 一跨四层钢框架Fig.2 One-bay-four-story steel frame

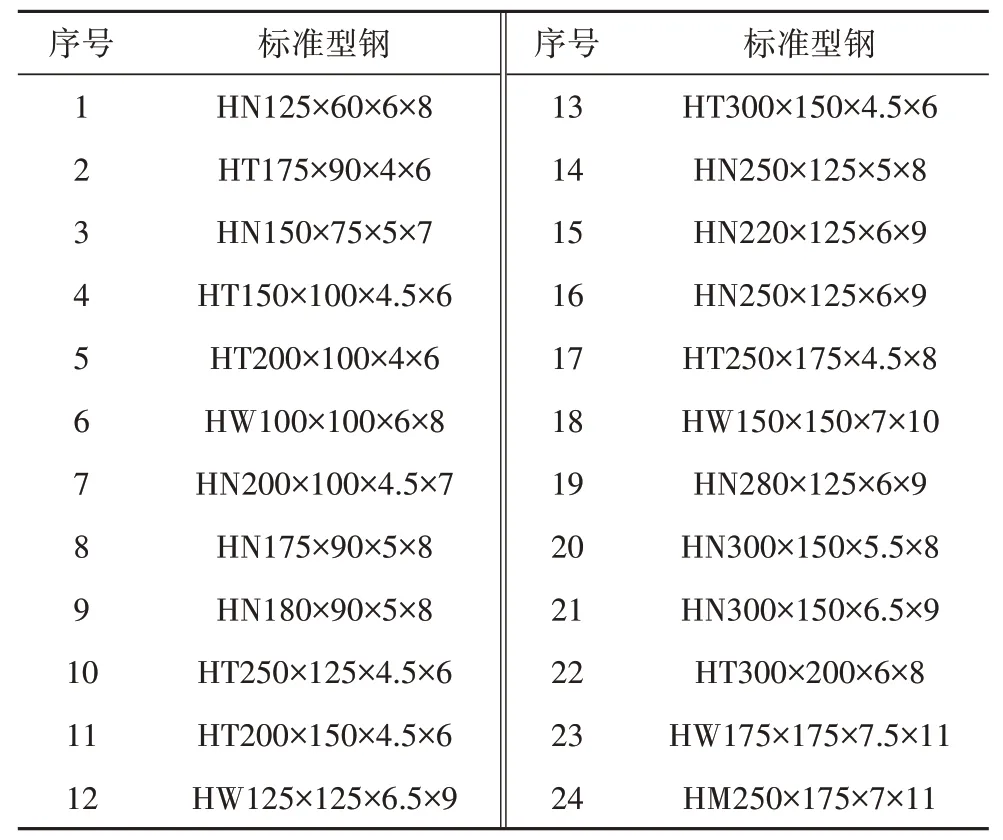
表1 H型钢Tab.1 H-shaped standard sections

采用枚举法计算离散优化问题的全局最优解，并验证所提出方法求解优化问题的理论下界的能力.为判断所提出方法的计算效率，再用遗传算法（Genetic Algorithm，GA）求解当前优化问题.GA是一种经典的智能优化算法，可依概率收敛到优化问题的全局最优解，因此采用GA 与所提出方法进行对比.采用MATLAB 平台自带的ga 求解器作为GA 的实现，其中：种群大小为30，最大迭代次数为500，其余参数都采用默认值.将GA 独立运行30 次，得到最佳的优化结果.

为了对关联离散变量进行线性松弛，需要定义包含离散点集的凸包.对于平面内的离散点集，可采用经典的Graham扫描算法［24］获得对应的凸包.

所有的优化计算都在MATLAB 平台中编码，并在一台工作站中执行.该工作站含双核2.2.GHz Xeon处理器，运行内存为32 GB.

3.1 柔度约束的最小体积问题

采用MOSEK 求解松弛的半定规划问题，得到松弛最优解.采用枚举法求解该离散优化问题，得到离散的全局最优解，并采用GA 得到近似最优解.松弛最优解对应的结构体积为0.137 8 m3，结构柔度为25.00；离散全局最优解对应的结构体积为0.141 4 m3，结构柔度为24.96；GA 得到的近似最优解对应的结构体积为0.142 0 m3，结构柔度为24.75.显然，松弛最优解比离散全局最优解略小，松弛最优解成为了离散优化问题的理论下界.同时，根据松弛最优解进行邻域搜索，可以快速得到高质量的离散可行解，甚至是离散的全局最优解.

基于半定规划的方法仅需要采用调用一次优化求解器、耗时0.51 s，就可以得到优化问题的理论下界，而枚举法需要求解524（≈5.96×1016）个子问题、耗时1 724.21 s，才能得到离散的全局最优解.为了得到近似最优解，GA 需要独立运行多次，而每一次运行的计算时间都超过1 s（介于1.10 s到2.00 s之间），所以，GA 的计算效率也远不如所提出的半定规划方法.显然，当需要判断某种算法的优化结果是否为全局最优时，半规划方法可以是一种高效的验证方法，尤其是对于规模稍大一些的同类优化问题.

松弛最优解和离散最优解在空间中的分布情况如图3所示，离散最优解如表2所示.

图3 柔度约束问题最优解的分布情况Fig.3 Distribution of optimum solution for compliance-constrained problem

表2 柔度约束问题的离散最优解Tab.2 Optimum solution for compliance-constrained problem

3.2 体积约束的最小柔度问题

采用MOSEK 求解松弛的二阶锥规划问题，同时采用枚举法求解离散优化问题的全局最优解，并采用GA 得到近似最优解.优化结果如下：松弛最优解的最小柔度为17.74，结构体积为0.180 0 m3；离散全局最优解的最小柔度为18.09，结构体积为0.179 0 m3；GA 得到的近似最优解对应的结构柔度为18.00，结构体积为0.180 1 m3，略大于体积上限.因此，对于体积约束的最小柔度离散优化问题，采用二阶锥规划的方法也可以得到离散问题的理论下界.可以根据松弛最优解进行邻域搜索，得到离散优化问题的可行解.

同样的，基于二阶锥规划方法仅调用一次优化求解器、耗时0.67 s，就能够得到离散优化问题的理论下界，而采用枚举法需要计算524（≈5.96×1016）个子问题、耗时1 605.13 s，才能得到离散的全局最优解.为了得到近似最优解，GA 需要运行多次，而每一次运行的计算时间都超过0.70 s（介于0.70 s 到1.50 s之间），所以，二阶锥规划方法的计算效率远高于枚举法和GA.

松弛最优解和离散全局最优解在空间中的分布情况如图4所示，离散最优解如表3所示.

表3 体积约束问题的离散最优解Tab.3 Optimum solution for volume-constrained problem

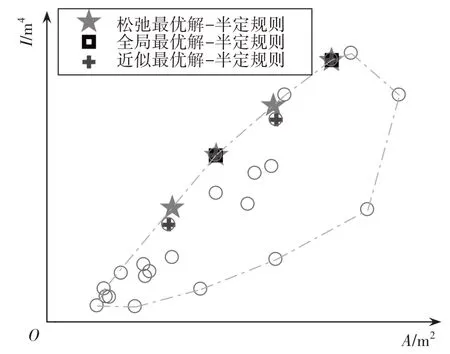
图4 体积约束问题最优解的分布情况Fig.4 Distribution of optimum solution for volume-constrained problem

4 结论

针对两类典型的钢框架结构离散优化问题，即柔度约束的最小体积问题、体积约束的最小柔度问题，进行了研究并得到如下结论：

1）基于凸组合的线性松弛方法，可以实现离散设计变量的线性松弛，使结构的刚度矩阵成为设计变量的线性函数，从而可将柔度约束的最小体积问题转化为松弛的半定规划问题，将体积约束的最小柔度问题转化为松弛的二阶锥规划问题.对这两类松弛的凸规划问题，可以快速得到全局最优解，即离散优化问题的理论下界.

2）基于松弛的半定规划方法和二阶锥规划方法，可以高效求解柔度约束的最小体积问题、体积约束的最小柔度问题，且求解效率远高于枚举法.因此，采用松弛的半定规划方法和二阶锥规划方法，可以快速验证某种优化方法是否得到全局最优解.

需要说明的是，基于凸组合的线性松弛方法实现了杆件的截面面积和惯性矩的线性化描述，但未能对其他截面属性进行线性化描述.因此，本文的优化方法适用于仅考虑杆件的拉压变形和弯曲变形的平面钢框架结构.