邓洪高，程 归，纪元法，孙希延

(桂林电子科技大学，广西 桂林 541004)

1 引言

随着北斗全球组网的成功，中国的卫星导航定位技术进一步提升。然而，在利用卫星通过载波相位实现高精度定位时，载波相位的整数部分是一个未知的随机整数，称为整周模糊度，需要在计算载波相位之前进行固定[1]。根据国际大地测量协会的统计，早在20世纪80年代初，整周模糊度的解算方法就已经被提出[2]。在1981年，Counselman提出了模糊度函数法(Ambiguity Function Method，AFM)，该方法具有对周跳不敏感的优点，但是计算效率有待提升[3]；静态模糊度快速解法(Fast Ambiguity Resolution Approach，FARA)是E.Frei和G.Beutler提出的，采用数理统计代进行数据预处理，在静态处理上有着显著效果，但是该方法在动态处理中并不适用[4]。LAMBDA(Least-Square Ambiguity Decorrelation Adjustment)算法是由Teunissen提出的经典算法[5，6]，LAMBDA算法具有良好的解算能力，但是算法中的搜索部分属于遍历搜索，搜索效率可以进一步提高；在Teunissen的基础上，后人针对搜索效率问题提出MLAMBDA-LAMBDA算法[7]，有效提高了整周模糊度的解算效率。由于整数模糊度的解决方案是从实数区域到整数区域的非线性映射，所以可以围绕浮点解设置一个整数解决方案集合，使用全局搜索来固定整周模糊度。本文基于标准差分进化算法(Differential Evolution Algorithm，DE)的强大全局搜索能力和快速收敛能力，对差分算子进行了自适应调整，避免了早熟，中断等问题，并通过ratio值对搜索完成的固定解进行质量检验。

2 载波相位双差模型

2.1 构建载波相位双差模型

在GNSS精密定位中，假设有卫星信号接收机r，b，在某时刻同时观测到i，j两颗卫星，则双差观测方程如下

(1)

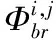
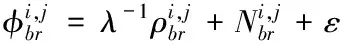
(2)

通过双差观测模型可知，一个双差载波相位观测方程有3个未知数，而每多一个共视卫星将会多一个双差整周模糊度，所以，在可用共视卫星较多的情况下，会导致多维整周模糊度，而多维整周模糊度的解算也是一个难点。

2.2 浮点解求解与处理

同时，对于短基线的实时定位来说，事先利用精密测量取得基线向量的精确值，可以有效地缩小搜索空间范围[10]。在基线长度为l对应的双差整周模糊度的取值范围如下

(3)

(4)

(5)

图1 定位流程简图

3 自适应加权的DE算法

3.1 标准DE算法

DE算法是由Kenneth Price和Rainer Storn最先提出的，其本身是一种随机模型，通过反复迭代以保存适应环境的个体。同时，DE特殊的记忆能力使其可以动态跟踪当前的搜索情况调整其搜索策略，具有较强的全局收敛能力和鲁棒性[11]。标准DE算法的主要流程如下：

1) 初始化

首先确定差分算法的控制参数，包括种群大小Popsize，最大迭代数Max＿generation，加权因子F和交叉概率CR。

2) 编码

实数编码是DE算法的特点所在，相较于二进制编码，两者均能够有效的搜索的双差整周模糊度固定值，但二进制编码无法反映问题本身的固有结构特点，个体长度较大，稳定性低于实数编码，也无法避免hamming悬崖问题。

3) 适应度函数

适应度函数是利用最小二乘准则，用模糊度浮点解去拟合固定解，使得浮点解达到在最小二乘准则下整数最优。在最小二乘准则下，代价函数为

(6)

适应度函数为

f(N)=b-lg(J(N))

(7)

4) 变异

一个变异个体的产生是根据变异公式vi，g=xr1，g+Fi，g*(xr2，g-xr3g)，其中i≠r1≠r2≠r3，F是控制差异变化的整数常量，通常取值为[0，2]；

5) 交叉

6) 选择

7) 更新

将更新之后的个体作为新的种群，重新迭代，重复4-7，直到满足终止条件或者最大迭代数。

3.2 标准DE算法中存在的问题

DE算法是根据父代个体间的差分矢量进行变异、交叉和选择操作，尽管在非线性优化问题上有强稳健性，但是同样容易由于本身的最优聚集性质而陷入早熟。当算法控制参数F，CR等设置不当的时候，一旦将其应用于整周模糊度解算中，即便是单频单模情况下，即模糊度维数较低的情况下，也会陷入早熟或者停滞问题。而在实际情况中，卫星数目的更迭导致模糊度维数的变化对于标准DE算法而言，更是无法适用。针对以上问题，提出了一种新的AWDE算法。

3.3 AWDE算法

新的AWDE算法，在进行固定模糊度之前，先对浮点解与协方差矩阵进行降相关处理，以增加算法的搜索效率；在DE算法之中，对迭代情况进行实时的评估，变异算子，交叉算子，种群大小均是随着种群适应度进行自适应调整。在搜索开始，变异和交叉算子较大，较大交叉算子和种群能够使得全局搜索的范围更大，较大的变异算子能够丰富种群多样性；而在迭代后期，种群所有个体的适应度都较高，此时，较小的交叉算子变异算子能够使迭代更快收敛，较小种群数量能够使得种群迭代的速度更快。在算法搜索完成之时，对此时的搜索值进行ratio值检验，用于判断算法是否陷入局部最优解。具体改进如下：

1)降相关

采用DE算法的实质是从搜索近似全局最优解来代替最优解，所以浮点解之间的强相关性将使搜索过程变得复杂。本文采用逆整数Cholesky变换对协方差矩阵进行降相关处理，在进行降相关处理后，适应度函数分布由原本的非单调函数变成了只有一个极值的单调函数[12]，从而降低了算法陷入局部最优的可能性。

2)变异

变异式vi，g=xr1，g+Fi，g*(xr2，g-xr3g)，更一般的可以写成如下形式

vi，g=Ai，g*xr1，g+Fi，g*(xr2，g-xr3g)

(8)

式中，i和r代表种群中的个体，g是迭代次数；Ai，g是对个体xr1，g的加权因子；于是针对于加权因子Ai，g和Fi，g提出的自适应改进为

(9)

Fi，g=0.5*(1.5-pi，g)

(10)

其中，i=[1，2，…，Popsize]，Popsize是种群大小，g是迭代数，ni是第i个个体未更新的次数，max是个体允许的最大未更新次数。其中pi，g的值为

(11)

其中，maxF(xg)代表在第g代中，最优个体的适应度函数值。通过pi，g来对种群适应度情况进行判断。对加权因子Fi，g的变化可以使得算法在种群整体适应度较差时，将变异个体迅速重新迭代得到更好的变异个体；而在种群适应度好的时候，可以使得变异个体与原个体差别减小，从而使得算法快速收敛。

3)交叉

标准DE算法采用的是贪婪策略。贪婪策略虽然有利于加快算法的收敛速度，但是其本质是逐渐向某最优值靠拢，导致了种群多样性的减小，即导致了早熟收敛的风险。好的搜索策略应该是在搜索初期保持着搜索空间的完整性，以确保包含最优解，而在搜索阶段的后期，应当加快搜索能力，增加搜索效率。新的交叉策略如下：

CR=CRmin+time(CRmax-CRmin)/Max＿generation

(12)

式子中CRmin为最大交叉率，CRmax为最小交叉率，time为当前迭代次数，Max＿generation为最大迭代次数。

4)种群大小变化

由于在解算整周模糊度固定解时，每个历元所观测到的卫星数是变化的，而可用共视卫星数目越多，所形成的双差载波相位方程也就越多，浮点解的维数也就越多。在模糊度搜索过程中，高维问题一直是难点。在DE算法中，不确定的浮点解意味着不确定的个体维数，当种群数量较小，浮点解维数较高时，极易陷入局部最优解；虽然可以通过增大种群数量解决这一问题，但是种群数量过大时，又会导致搜索效率降低。在本文中，初始种群数量的大小由个体维数确定，即popsize = 4*Dim，同时初始种群的分布采用均匀设计，后续种群数量将随着种群适应度的提高而缩小。

5)质量控制

由于智能优化算法本身是通过交叉，变异等方法去用全局近似最优解去拟合全局最优解，这就导致了算法本身具有一定的不确定性。而在实际情况下，由于可用共视卫星变动导致双差整周模糊度维数的频繁变化在一定程度上增大了这种不确定性。所以，解算之后的质量检测尤为重要。Ratio值检验法是以固定解中次优解和最优解的残差平方和的比值作为检验值，将其与设定的阈值比较，阈值通常取2或3，当ratio值大于阈值时，判定模糊度固定解正确[13]。

图2 AWDE算法流程图

4 算例与分析

4.1 算例1(3维情况下六种算法对比试验)

本例将对上述六种模糊度固定方法进行仿真，比较相互的解算性能。选取3维的双差载波相位方程的模糊度浮点解和协方差矩阵为

通过高斯整数变换进行降相关之后，浮点解和协方差矩阵为：

初始种群大小为Popsize=4*3=12，DE算法终止迭代数为50，基线长度为1米，遗传算法终止迭代数为100，利用简单遗传算法GA，自适应遗传算法AGA，LAMBDA算法MLAMBDA-LAMBDA算法，标准DE算法和AWDE算法对整周模糊度进行搜索和比较。仿真结果如下图所示。

图3 简单GA算法 图4 AGA算法注：图中红色表示最大适应度，绿色表示平均适应度，蓝色表示最小适应度，下图一致

简单遗传算法的参数需要在解算整周模糊度之前需要根据模糊度浮点解和协方差矩阵进行适应性调整，当参数不合适时，算法效果十分差。而且由于其遗传算子的值是固定值，没有办法随着迭代而更新，导致算法容易陷入停滞与早熟；在算法迭代至最优值解时，又无法及时降低交叉变异概率，增加了解算时间。经过对遗传算子进行自适应调整之后，算法能够准确的迭代出全局最优解，但是搜索效率和成功率还有提升空间。

图5 DE算法(未降相关) 图6 DE算法(降相关)

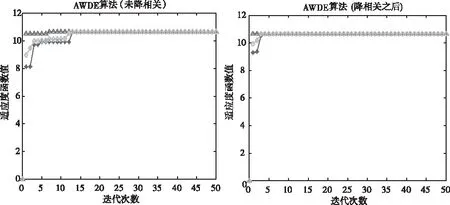
图7 AWDE(未降相关) 图8 AWDE(降相关)

通过对标准DE算法和AWDE算法分别进行了降相关和未降相关的比较，如图5，6，7，8所示。在经过降相关之后，标准DE算法的收敛代数由23代左右升级到了17代左右，AWDE算法由12代升级到了7代左右。从图中可以明显看出，在经过降相关之后，AWDE算法的最小适应度并未陷入局部最优，减少了解算时间，提高了搜索效率。

在采用自适应加权的DE算法之后，对于3维双差整周模糊度，在10次迭代以内就能准确解算出全局最优解，算法具有良好的全局搜索能力和较快的收敛速度。即使在未降相关的情况下，也不会陷入局部最优解。

为了准确统计算法的准确性和可靠性，对3维双差整周模糊度用以上六种算法进行100次的重复试验，最大迭代次数为50代。对比各算法的解算时间与解算成功率，统计结果如表1所示。

表1 六种算法对比情况

为了更加直观的展示每一次试验的解算时间，将DE，AWDE，AGA算法的运算时间用柱状图显示如图9所示。

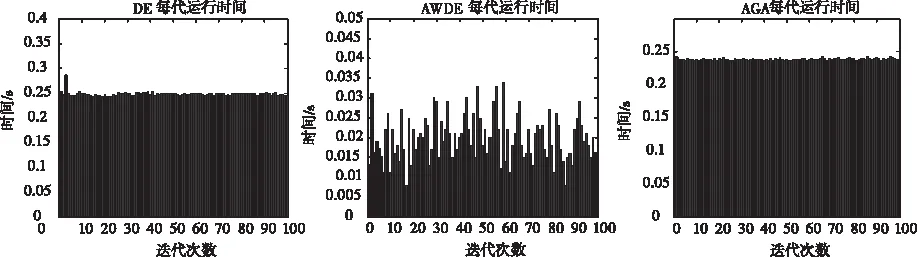
图9 各算法运行时间比较图

从上面的图表可知，在六种算法中，AWDE算法有着99%的解算成功率和0.0142秒的解算时间。而GA算法由于本身的不稳定，统计结果无效，DE算法的成功率只有86%，AGA算法的成功率达到了96%，但是平均解算时间到了0.2459秒。AWDE相对于LAMBDA算法和MLABDA-LAMBDA算法，解算成功率相差无几，但是解算时间比LAMBDA和MLABDA-LAMBDA算法分别快了0.0479秒和0.0083秒。

同时，在AWDE算法中加入了ratio值检验，检验阈值为2，当每次检验的ratio值大于或等于阈值时，代表固定解可用。在本次的100次重复实验中，检验结果如图所示，在100次的迭代试验中，只有刚开始的第一次ratio值小于检验阈值，解算成功率达到了99%。

图10 3维下的AWDE算法100代ratio检验

4.2 算例2(多维解算实验)

对于目前最常用的单频接收机ublox接收机来说，为保证低成本与高精度，通常采用单频双模工作模式，理论上最大卫星数为59颗(北斗35颗，GPS24颗)，而在实际观测中，单频双模接收机能够获得20颗左右的可用共视卫星。

图7 一天内观测到的卫星数

而随着可用共视卫星的增多，意味着浮点解维数的增加，对固定模糊度的难度增加。所以在此算例中选取了3维，6维，12维的双差模糊度进行解算速度和可靠性的比较，其中3维浮点解与算例1一致。6维浮点解和12维浮点解分别为：

9.9955 -43.0015]T

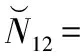
-297.6589 -22201 51236 30258 3899.4

-22749 -159.2788]T

解算结果如下所示：

图12 6维AWDE 图13 12维AWDE

表2 AWED算法在不同维数下的比较

通过上述图表可以看出，随着维数的增长，双差整周模糊度的解算难度增加。6维，12维的平均收敛代数变成了11代和20代，解算时间也由3维的0.0142秒增长到0.0352秒和0.1659秒，解算成功率有稍微下降，但是解算速度和精度依旧能够满足解算的实时性。

5 结语

DE算法具有很强的全局搜索能力和极快收敛速度，但是由于本身的贪婪算法和差分加权本质上属于寻优迭代，且本身的变异，交叉因子，种群数量均是定值，无法满足实际解算中的变化情况，更无法适应双模甚至三模情况下的多维模糊度情况。本文针对整周模糊度解算问题对迭代算子进行自适应优化，并通过ratio值进行解算质量控制。实验结果表明，改进后的AWDE算法在有效性和稳定性方面均有不错的表现。