邓天舒

(清华大学高等研究院,北京 100084)

非厄米趋肤效应是近几年非厄米物理研究领域中的热点问题,它揭示了非厄米系统中体态波函数和能谱计算会敏感依赖于边界条件的新奇现象.人们提出广义布里渊区的概念用以刻画非厄米系统中的体态波函数和能带性质.基于广义布里渊区计算的非布洛赫拓扑数可以重新构建非厄米拓扑体边对应关系.然而,过去关于非厄米趋肤效应的讨论主要针对开放边界条件,如果采用畴壁边界条件,广义布里渊区和非布洛赫拓扑数的计算都需要重新考虑.本文综述了近几年关于畴壁边界条件下非厄米趋肤效应的若干研究工作,首先从一般的一维非厄米单带模型出发,推导广义布里渊区方程的一般形式;然后回顾了非厄米SSH (Su-Schieffer-Heeger)模型中广义布里渊区和非布洛赫拓扑数的计算;最后在一维光量子行走的系统中,介绍了实验上非厄米趋肤效应的实现和非厄米拓扑边缘态的探测.

1 引言

在孤立的量子系统中利用厄米型的哈密顿量来研究物相的基本性质是量子物理研究的基本范式.然而实际上,绝对孤立的系统是不存在的,因此人们发展了一系列理论用于描述与环境有相互作用的系统的演化,其中一个最为经典的描述就是在马尔科夫近似下得到的Lindblad 量子主方程[1,2].量子主方程的研究常常需要涉及到非厄米的哈密顿量: 一方面,在忽略量子跃迁效应时,Lindblad型主方程可以直接近似为非厄米哈密顿量下的薛定谔方程[3,4];另一方面,如果把密度矩阵映射为双希尔伯特空间的波函数,那么其在主方程下的演化可以严格映射为双空间波函数在非厄米哈密顿量下的演化[5—7].相较于量子主方程,非厄米哈密顿量的描述在形式上显得更为简洁,将之与传统厄米哈密顿量中的各种经典理论结合,就有可能建立新的理论框架,做出新的理论预言.如非厄米拓扑能带理论的发展就是将非厄米哈密顿量与传统拓扑能带结合的典型范例[8—12].此外,近年来随着实验技术的发展,人们有能力在越来越多的物理系统中模拟非厄米哈密顿量[13—19],这进一步促使人们探索非厄米系统中的种种新奇现象.其中广受关注的一个成果就是关于非厄米趋肤效应的研究[20—25].

非厄米趋肤效应指的是在非厄米系统中,体态波函数局域在边界附近的现象.为了刻画这种效应,需要将传统的布洛赫能带理论修正为非布洛赫能带理论.以一维系统为例,在传统的布洛赫能带理论中,无论是开边界条件还是周期边界条件,体态波函数都满足布洛赫波的形式ψ(x)=eikx.然而在非厄米系统中,周期边界条件下的体态波函数依然是布洛赫波;但是对于存在边界的系统,波函数有可能会局域在边界附近,其体态波函数会满足ψ(x)=βx的形式,其中β=reik,r和k都是实数.这里的β会在复平面内形成一条封闭曲线,被称为广义布里渊区.在不同的系统中,不同边界条件下求解这条封闭曲线的方程被称为广义布里渊区方程.基于广义布里渊区可以正确地计算不同边界下的实空间连续谱,即非布洛赫能带.非布洛赫能带理论最初的一个成功应用就是在非厄米拓扑问题中.在广义布里渊区上做积分得到的非布洛赫拓扑数,可以正确地预测系统中拓扑边缘态的产生与消失,而布洛赫拓扑数做不到这一点[21].这一案例表明,广义布里渊区和非布洛赫能带理论对理解和描述非厄米系统有着重要的意义.

非厄米趋肤效应被提出以来就吸引了凝聚态理论各界的广泛关注,非布洛赫能带理论取得了蓬勃发展,出现了很多重要成果[26—43],如开边界条件下一维系统中广义布里渊区方程的一般形式[26]量子主方程中的非厄米趋肤效应[32,34,37,38]、非厄米趋肤效应的拓扑起源[29,30]等.以上绝大多数的讨论都是针对开边界条件,而广义布里渊区方程对边界条件的依赖非常敏感,所以此时研究多种不同边界条件下的广义布里渊区是十分重要且必要的.本文重点关注畴壁边界条件下的非厄米趋肤效应[17,44].畴壁边界条件指的是把两块不同参数的材料拼接在一起形成的一种空间结构,在拓扑能带理论研究中有着广泛的应用[45—47].一方面,在该系统中研究广义布里渊区可以帮助构建畴壁边界条件下的非厄米体边对应关系;另一方面,在很多量子模拟的实验系统中,畴壁边界条件比开边界条件更容易实现(如光量子行走系统),因此对畴壁边界条件下非厄米系统的深入研究也为实验实现非厄米趋肤效应提供了更多的可能.

本文分为以下几个部分对畴壁边界条件下非厄米趋肤效应的相关研究展开综述: 第2 节介绍在一般的一维单带紧束缚模型中,广义布里渊区方程的推导;第3 节以非厄米SSH (Su-Schieffer-Heeger)模型为例,介绍畴壁边界条件下非布洛赫能带理论的应用,以及非厄米拓扑体边对应关系的构建;第4 节探讨非厄米趋肤效应在一维量子行走体系中的实现方案,并再次应用非布洛赫能带理构建非厄米拓扑体边对应关系,最后讨论实验上对拓扑边缘态的探测.

2 畴壁边界条件下广义布里渊区的计算

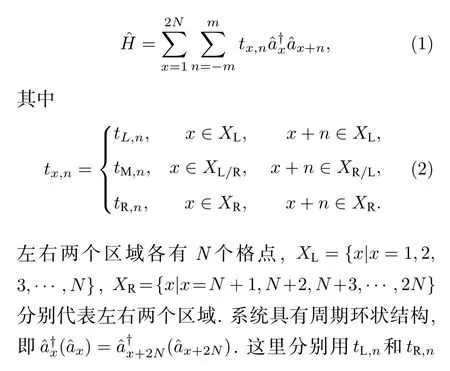
本节从一维单带模型出发,推导畴壁边界条件下的广义布里渊区方程.考虑由两个区域组成的一维单带模型,两个区域在边界拼接到一起,形成畴壁边界条件.如图1 所示,其哈密顿量可写作代表左右两个区域内部相差n个格点的跃迁,m代表最大跃迁幅度.而tM,n代表所有跨越边界的跃迁.图2 给出了该模型中哈密顿量的所有本征波函数分布图,可以看到,当,哈密顿量是非厄米的,波函数局域在了两个畴壁附近,即非厄米趋肤效应.在远离边界的左边(右边)区域内部,系统具有平移对称性,实空间波函数可分别表示为这里的βx可视作厄米哈密顿量中布洛赫波形式 eikx的推广.对于给定的能量E,通过分析实空间的薛定谔方程可以得到特征方程hα(βα)=E,其中

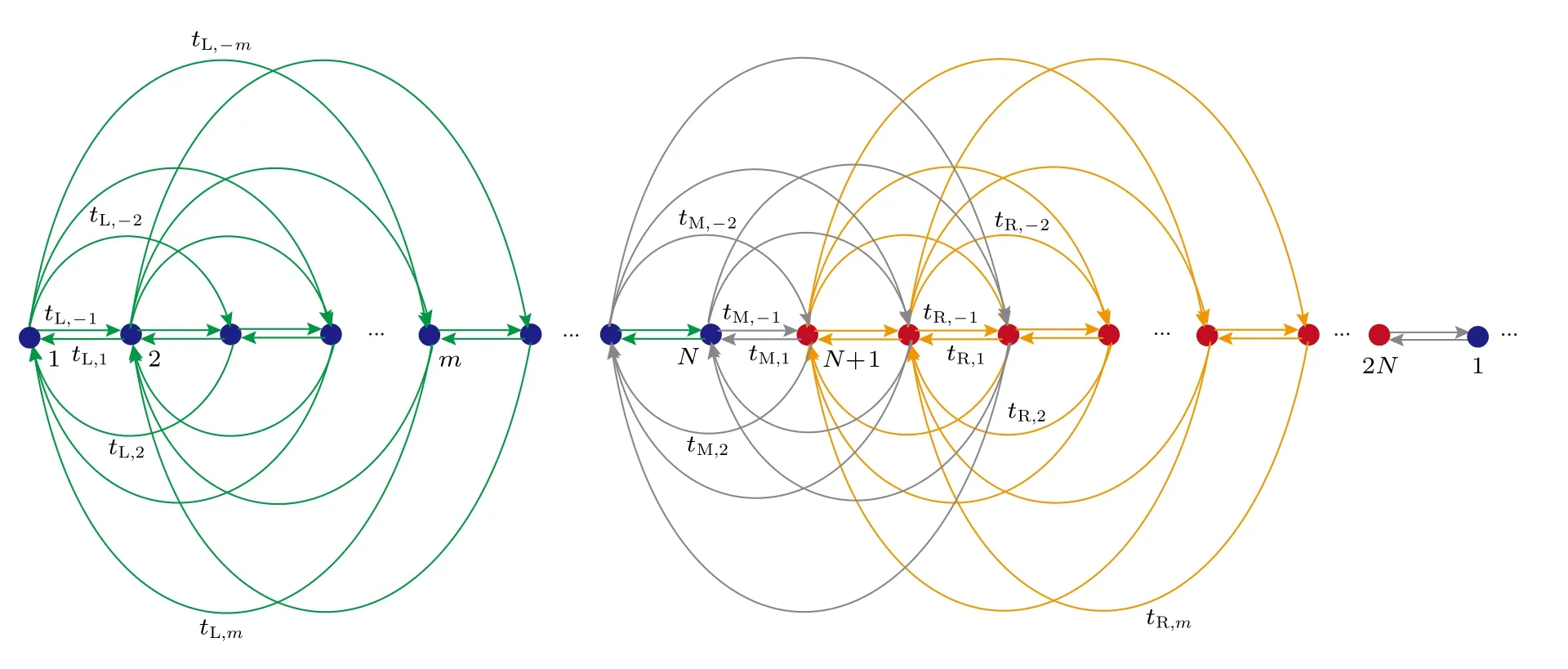
图1 畴壁边界条件下的一维单带模型示意图,格点首尾相连形成环状结构.跃迁距离最远为mFig.1.Illustration of single-band lattice model under domain-wall configuration.The hopping distance is m at most.

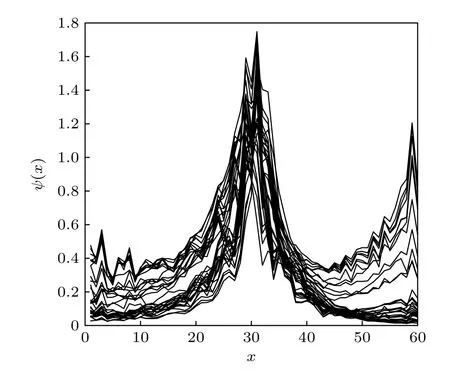
图2 波函数在实空间的分布图.其中 m =2,tM,1=tM,2=tM,-1=tM,-2=1,t L,-2=4,t L,-1=-1,t L,1=3,tL,2=2,t R,-2=2,t R,-1=1,t R,1=3,t R,2=-2,N=30Fig.2.Wave-function distribution in real space.Here,m=2,t M,1=tM,2=tM,-1=tM,-2=1,t L,-2=4,tL,-1=-1,t L,1=3,t L,2=2,t R,-2=2,t R,-1=1,tR,1=3,t R,2=-2,N =30 .

其中,Cn(Dn)是通解中的待定系数.需要注意的是此时得到的通解形式只考虑了哈密顿量左右区域内部的跃迁tL,n和tR,n,而没有考虑跨越边界的跃迁tM,n.这是因为tM,n作用在了边界附近的 4m个格点,只有当讨论边界条件时才会引入tM,n的影响.

接下来把通解波函数代入到畴壁边界条件下的哈密顿量中,得到 4m个边界方程:

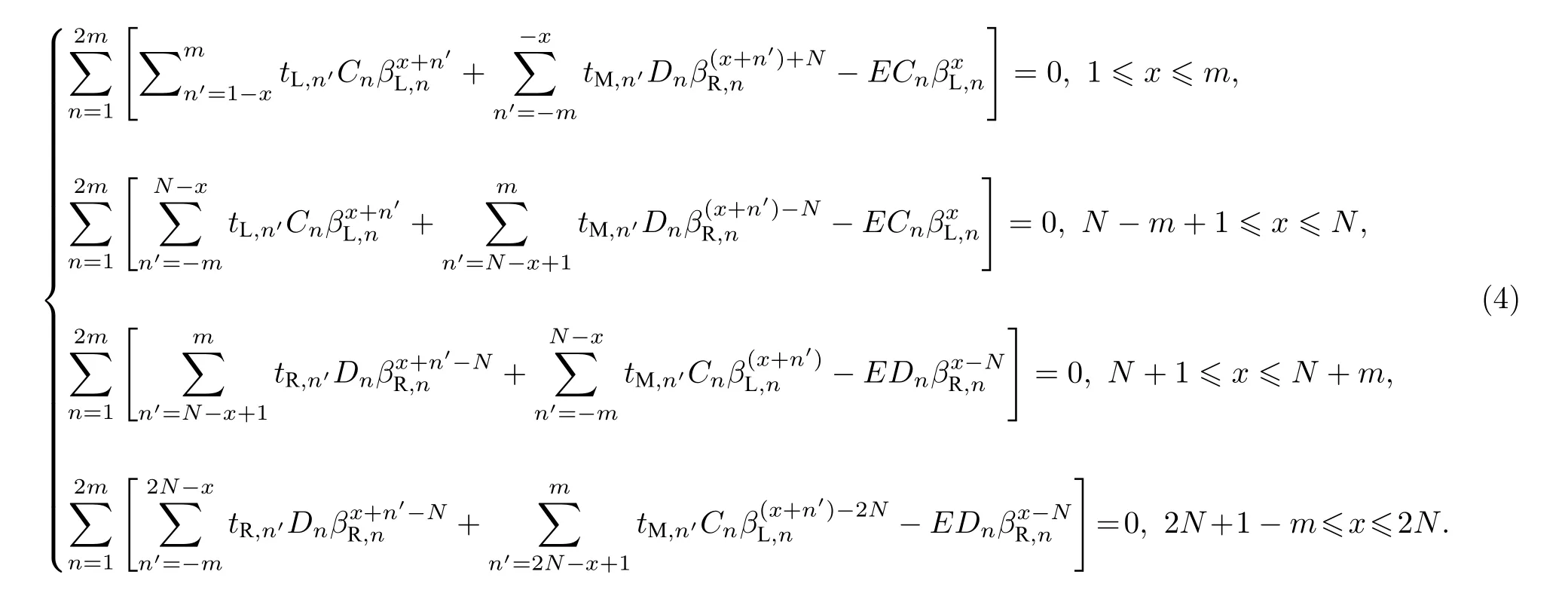
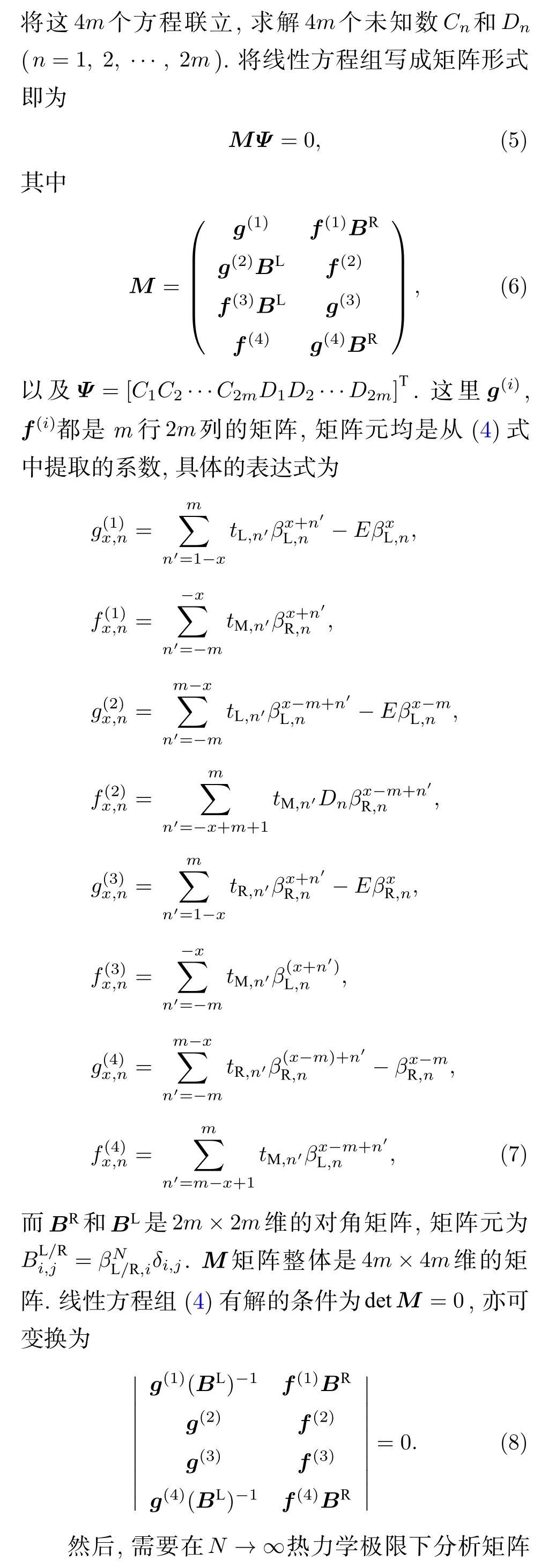
这里n=1,2,3,···,N,因此(12)式在热力学极限下可求得无穷多个解[21].综上,|η2m|=|η2m+1|即为广义布里渊区方程,据此可以求出畴壁边界条件下的广义布里渊区和非布洛赫能带的能量.值得注意的一点是,广义布里渊区的计算与tM,n参数的具体取值无关.这体现出广义布里渊区方程具有抗干扰性,只要两块材料在边界上相连,相连处跃迁参数的扰动并不会影响两块体材内部广义布里渊区的计算结果.

3 非厄米SSH 模型

本节将回顾畴壁边界条件下的非厄米SSH 模型[44].以此模型为例,具体阐释广义布里渊区的计算,并将之应用到非厄米能带理论中,计算非布洛赫能量和非布洛赫拓扑数,验证畴壁边界条件下非厄米系统中的体边对应关系.

3.1 模 型

如图3 所示,考虑畴壁边界条件下的非厄米SSH 模型.开边界条件下的非厄米SSH 模型过去有过许多讨论[48,49],而在文献[21]中首次利用广义布里渊区概念解释了该模型中反常的体边对应现象.而畴壁边界条件下非厄米SSH 模型的哈密顿量可写作

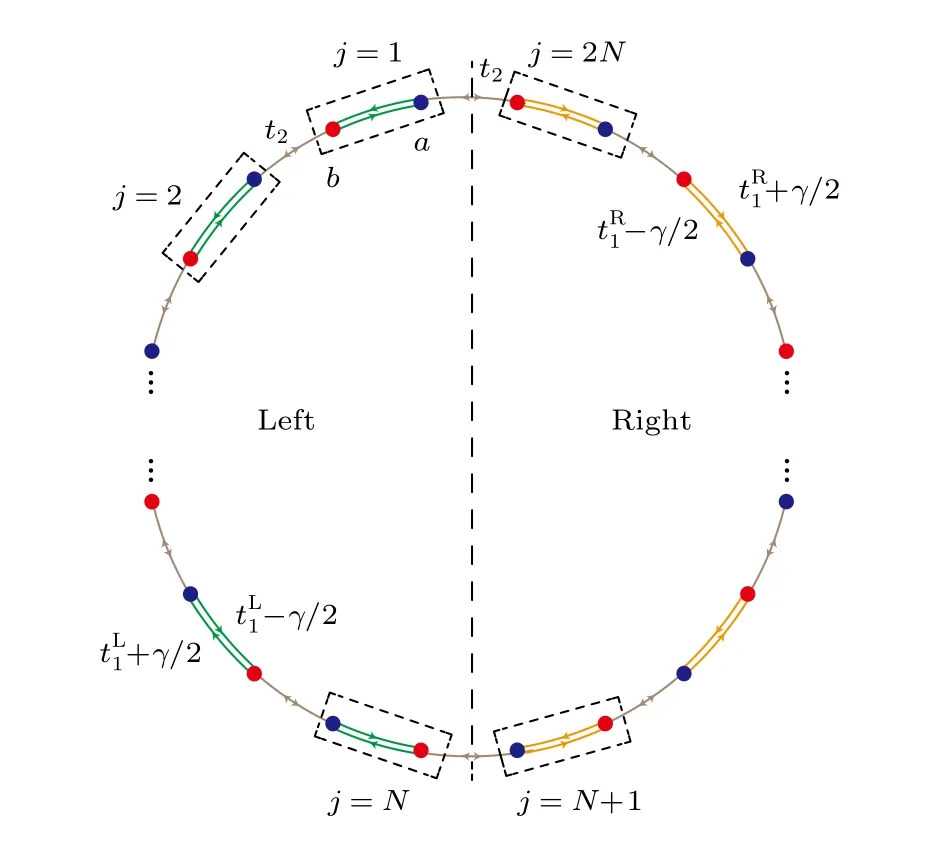
图3 畴壁边 界条件 下的非厄米SSH 模 型.在左边(右边)区域元胞内部a 子格到b 子格的跃迁是-γ/2,而元胞内部b 子格到a 子格的是 t L1(R)+γ/2 .此外,畴壁两边不同区域具有相同的 t2 和 γ [44]Fig.3.A non-Hermitian SSH model with two bulks.For left(right) bulk,the intra-cell hopping from a-site to b-site is-γ/2while the intra-cell hopping from b-site to asite is +γ/2 .Also,different bulks holds same t2 and γ[44].

该模型具有手征对称性σzh(k)σz=-h(k) 和非厄米趋肤效应,是一个探讨非厄米趋肤效应和非厄米拓扑能带理论的经典模型.开边界条件下的非厄米SSH 模型已经有过详细的讨论[21],在本节后面的部分,将集中讨论畴壁边界条件下非厄米SSH 模型中广义布里渊区的计算方法,并基于此构建非厄米拓扑体边对应关系.

3.2 广义布里渊区

本节采用第2 节中的方法,具体探讨广义布里渊区的计算.首先可以将实空间哈密顿量中特定能量的本征态写作

(18)式可化作一个关于β的一元二次方程,方程有两个根,所以(16)式中的nmax取 2 .

将(15)式,(19)式和(20)式代入边界条件:

由第2 节中相似的逻辑便可判断,体态的波函数解的数目一定正比于N,为了满足这一点,集合{ηi|i=1,2,3,4}中的元素一定满足

这就是畴壁边界条件下非厄米SSH 模型的广义布里渊区方程.(29)式与文献[44]中所给的广义布里渊区方程完全一致,是一个更为简洁的形式.

接下来详细阐述如何由广义布里渊区方程计算得到广义布里渊区和非布洛赫能带.形式上,(29)式是关于4 个变量βL,1,βL,2,βR,1,βR,2的方程.但是从(18)式可以看到,所有的ηi都由能量E决定,所以方程(29)中只有一个独立的复变量(在非厄米系统中E和β一般都是复数).因此在方程(29) 的约束下,便可确定任意一个βα,n在复平面内形成的封闭曲线.具体来讲,可以从βL,1=reip出发,先将完整的复变量βL,1=reip形式代入(18)式中,计算能量E,再通过能量计算βL,2,βR,1,βR,2.然后把求得的所有{1/βL,1,1/βL,2,βR,1,βR,2}进行排序,代入方程(29)中.于是方程(29)将变成一个关于r和p方程,遍历p∈[0,2π),便可得到r关于p的函数,由此便可绘制左边区域的广义布里渊区的其中一支解.依照此法可求得所有的βα,n.

图4(c)和图4(d)分别给出了左边区域和右边区域的广义布里渊区.在开边界条件下的非厄米SSH 模型中,广义布里渊区的方程写作|β1|=|β2|,因此β的两支解会在复平面内重合.仅将边界条件改为畴壁边界条件后,就会得到完全不同的广义布里渊区,这也印证了非厄米趋肤效应对边界条件变化的敏感性.

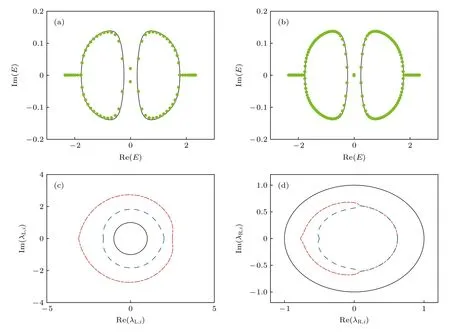
图4 (a),(b)体态波函数的理论(黑线)和数值(绿点)结果,(a)图的链长为 N =20,(b) 图的链长为 N =40 .(c) 复平面内βL,1(红色点划线)和 β L,2 (蓝色虚线)表示的左链的非布洛赫布里渊区.(d) 复平面内 β R,1 (红色点划线)和 β R,2 (蓝色虚线)表示的右链的非布洛赫布里渊区.在图(c)和图(d)中,取热力学极限 N →∞ 并且用黑色实线画出了布洛赫布里渊区作为对比.在所有的子图中,选取的参数为=-t2,=1.5t2,γ =1.33t2 [44]Fig.4.(a),(b) Theoretical (black lines) and numerical (green dots) results of bulk-state energy spectrum.The length of chain is N=20 for panel (a) and N =40 for panel (b).(c) Non-Bloch Brillouin zones of the left bulk,represented by β L,1 (red dash-dotted line) and β L,2 (blue dashed line) on the complex plane.(d) Non-Bloch Brillouin zones of the right bulk,represented byβR,1(red dash-dotted line) and β R,2 (blue dashed line) on the complex plane.In panels (c) and (d),we take the thermodynamic limit N →∞,and we also plot the Bloch Brillouin zones with black solid lines for comparison.For all subplots,we take =-t2,=1.5t2,γ =1.33t2 [44].

我们又将广义布里渊区与布里渊区 eik在复平面上形成的单位圆做对比.需要注意的是,在两种情况下,广义布里渊区会退化为单位圆.一种情况是当哈密顿量为厄米的γ=0,另一种情况是系统具有周期边界条件=.这表明非厄米趋肤效应是系统非厄米性与边界条件共同作用的结果.

此外,本文还基于广义布里渊区和特征方程,绘制了非布洛赫能带(见图4(a)和图4(b)),并将之与实空间严格对角化哈密顿量的能谱作对比.可以看到在N=20 和N=40 的情况下,数值计算的能谱和广义布里渊区的理论得到的非布洛赫能带符合得很好,并且随着N的增大,两者的差距变得更小.这充分说明本文计算得到的广义布里渊区在畴壁边界条件下可以精确刻画热力学极限下实空间的本征能谱.

3.3 非布洛赫拓扑数与拓扑体边对应关系

本节基于3.2 节得到的广义布里渊区,计算畴壁边界条件下的非布洛赫拓扑不变量,构建非厄米系统中的拓扑体边对应关系.由系统的布洛赫哈密顿量(14)可知,系统具有手征对称性,其拓扑不变量可以由Zak 相定义:

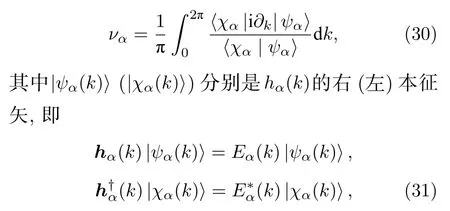
这里νL和νR分别代表左边区域和右边区域的拓扑数,两者之差如果非0,畴壁上就会出现边缘态,这就是传统意义上畴壁边界条件下的体边对应关系.但是对于非厄米系统来说,需采用非布洛赫能带理论,将积分区间从布里渊区修正为广义布里渊区.因此将β=r(p)eip和h(β) 代入(30)式便可得到非布洛赫拓扑数的计算公式:

需要注意的是,从图4(c)和图4(d)可以看出,广义布里渊区方程一般会求得r(p) 的两支解,也就是说(32)式中有两个可以选择的积分区间分别对应βα,1和βα,2在复平面上形成的封闭曲线.在非厄米SSH 模型中可以证明,同一个参数下求得的两个广义布里渊区上积分得到的非布洛赫拓扑数是一致的[44].

图5(d)—(f)分别把布洛赫和非布洛赫拓扑数和数值计算的能谱做对比,确认了非布洛赫体边对应性.在厄米的情况下γ=0,非布洛赫和布洛赫拓扑数的结果一致,即当时系统存在零模.随着γ增加,布洛赫和非布洛赫拓扑数之间的区别便显现出来,左右区域非布洛赫拓扑数的差值可以正确地预测边缘零模的出现与消失,而布洛赫拓扑数无法做到这一点.这进一步说明,相比于布洛赫拓扑数,基于广义布里渊区的非布洛赫拓扑数更能正确地判断系统拓扑性质的变化.

图5 (a)—(c)颜色栏在 - 平面能谱绝对值的最小值.这里选取 N =40 .图(a)中 γ =0,图(b)中 γ =0.67 t2,图(c)中γ=1.33 t2 .黑色线对应参数=,此时畴壁构型会退化回周期边界条件的均匀格点模型.玫红色的虚线对应的参数为=-.图(a)—(c)里的红色点划线给出了用在图(d)—(f)里的参数,即=1.5 t2 .(d)—(f)能谱绝对值(上部)和拓扑数(下部).图中下部给出了左链的布洛赫拓扑数 νL (玫红虚线) 和右链的非布洛赫拓扑数 ν R (黑色虚线),以及左链的非布洛赫拓扑数 (红色实线)和右链的非布洛赫拓扑数 (蓝色实线)[44]Fig.5.(a)—(c) Contour plots of absolute values of the energy-spectrum minimum on the -plane.Here,we take N =40 .We also take γ =0 for (a),γ =0.67 t2 for (b) and γ =1.33 t2 for (c).The black solid lines are given by =,where the domainwall configuration is reduced to single homogeneous bulk with a periodic boundary condition.The magenta dashed lines are given by =-.The red dashed-dotted line in panels (a)—(c) correspond to parameters we use in panels (d)—(f) with =1.5 t2 .(d)—(f) The absolute values of the energy spectrum (upper panels) and various winding numbers (lower panels).In the lower panel,we show the Bloch winding numbers for the left bulk νL (magenta dashed lines) and the right bulk ν R (black dashed lines),as well as non-Bloch winding numbers for the left bulk (red solid lines) and the right bulk (blue solid lines)[44].

此外,我们还发现,即使畴壁某一侧的参数不变化,其非布洛赫拓扑数的计算却依赖于广义布里渊区,进而会受到另一侧参数的影响.例如,图5(f)中右侧区域的非布洛赫拓扑数会在0.16 附近从 0 变化为 0.5,而此时右链的参数始终保持不变.这是畴壁边界条件下的非厄米系统又一个独特的性质.

4 一维量子行走体系中的非厄米趋肤效应

在第3 节讨论的非厄米SSH 模型中,已经从理论上推导了广义布里渊区和非布洛赫拓扑数,并基于此重新构建了非厄米系统中的拓扑体边对应关系.但是如何在实验系统中模拟非厄米趋肤效应并验证非厄米体边对应关系,依然是一个重要的问题.本节将介绍如何在一维光量子行走的实验平台中模拟具有非厄米趋肤效应的有效哈密顿量,并在该模型中讨论广义布里渊区和非布洛赫拓扑数的计算,再次验证非厄米体边对应关系[17].

4.1 模 型

量子行走是一类高度可控的周期驱动系统,被广泛应用于量子算法[50,51]和量子模拟[52—55]的研究.近些年来,人们开始致力于在离散量子行走平台中模拟和研究非厄米拓扑相[56—58],这为研究具有非厄米趋肤效应的拓扑非平庸模型提供了一个良好的基础.

在量子行走系统中,选定如下的非幺正时间演化算符:

通过对角化实空间的时间演化算符,得到了所有的本征态波函数,如图6(b)所示.可以看到,随着γ的增加,体态波函数会渐渐局域在畴壁边界附近.由此可以判断系统具有非厄米趋肤效应.该模型还具有手征对称性,σxUσx=U-1,所以也可以在其中探讨非厄米拓扑相变和体边对应关系.接下来将在第4.2 节讨论该模型中的广义布里渊区的计算,在第4.3 节讨论非布洛赫拓扑数的计算.

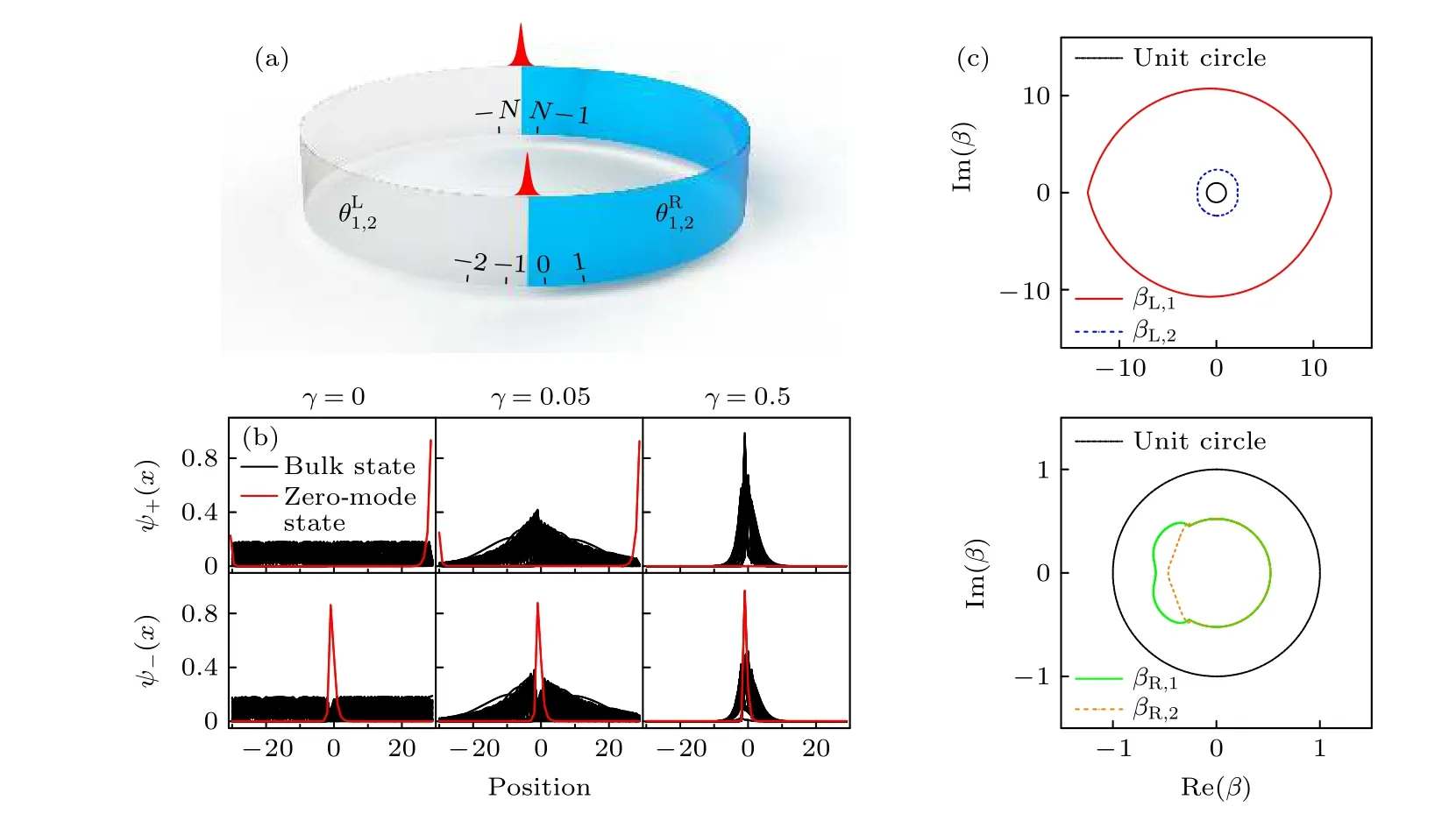
图6 具有非厄米趋肤效应的量子行走 (a) 畴壁边界条件示意图;(b) 体态波函数(黑色)和边缘态波函数(红色)的空间分布,其中是手征对称算符的本征态;(c) 左边(右边)区域的广义布里渊区 β L(R),i,i=1,2 代表 β 有两支解.标准的广义布里渊区是单位圆(黑色实 线).参数选取为 N =30 ,=0.1875π,=-0.3333π,=0.2π,=-0.6667π,以及 γ =0.5 [17]Fig.6.Quantum walks with non-Hermitian skin effect: (a) Schematic illustration of the domain-wall configuration.(b) Spatial distribution of the projected norms of bulk (black) and edge (red) states,withare eigenstates of the chiral-symmetry operator.(c) Generalized Brillouin zones for left (right) bulk β L(R),i,i =1,2 indicates two solutions of β .Whereas the standard Brillouin zones are indicated by unit circles (solid black line).Parameters: N =30,=0.1875π,=-0.3333π,=0.2π,=-0.6667π,γ=0.5 [17].

4.2 广义布里渊区的计算

为了计算广义布里渊区,先给出波函数本征态的通解形式:

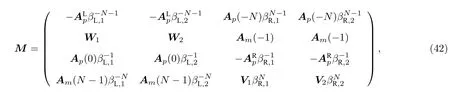
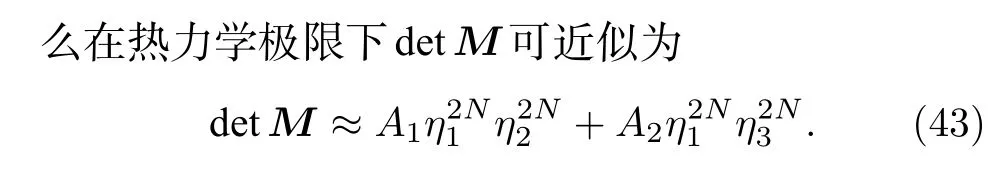
于是便可得到形式上与(29)式完全一样的广义布里渊区方程,并可按照3.2 节中的方法求解广义布里渊区.图6(c)给出了左右区域广义布里渊区的例子.

4.3 非布洛赫拓扑数与体边对应关系

接下来,基于广义布里渊区,计算量子行走模型中的非布洛赫拓扑数.需要注意的是,量子行走是周期驱动系统,即使是对于传统的幺正时间演化算符,其拓扑性质与静态哈密顿量的情况也有所区别.对于静态哈密顿量,如系统满足手征对称性,那么其能谱一定是关于E=0 对称分布,能隙也一定出现在零能处.但是对于周期驱动的系统来说,其准能量分布在 [-π,π) 区间,如果系统有手征对称性,那么准能量不仅关于E=0 对称,也关于E=π对称,所以拓扑绝缘体的能隙会出现在准能量ε=0 和ε=π 两个位置.因此当系统处于拓扑非平庸区时,其边缘态能量会有 0 和 π 两个模式,相应地,也需计算 0 模和 π 模两种拓扑数ν0和νπ.关于Floquet 系统中的拓扑理论,在过往的文章中有过很多讨论[59—63].这里先对布洛赫拓扑数ν0和νπ的计算方法做简单介绍.首先可以定义另一个时间框架下的时间演化算符:

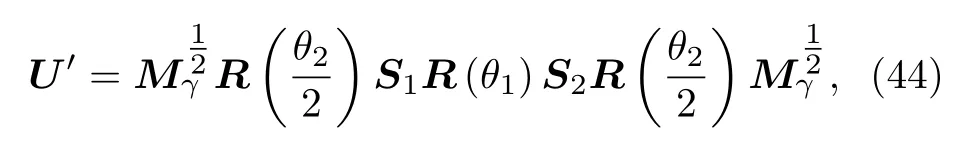
U′和U相当于选取了不同的时间起始点,他们具有相同的准能量能谱,都满足手征对称性,对称性算符均为σx.然后参照(30)式中的方法,分别计算不同时间框架下的布洛赫拓扑数ν和ν′.注意(30)式中的χk和ψk分别是时间演化算符的左右本征矢,定义为

对于传统的幺正量子行走系统,ν0(π)即可预测系统0(π)模的拓扑边缘态,但是在本文讨论的非幺正量子行走系统中,布洛赫拓扑数并不能正确地刻画非厄米系统中的拓扑性质,因此,还需根据广义布里渊区的计算结果和拓扑数的计算公式(32),计算不同框架下的非布洛赫拓扑数和,进而得到0(π)模的非布洛赫拓扑数:

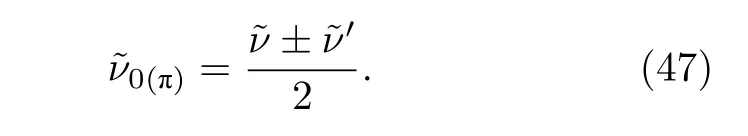
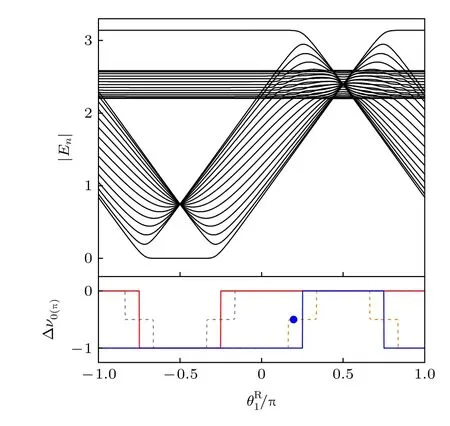
图7 黑色实线为准能量能谱,红色实线和蓝色实线分别代表零模拓扑不变量的差值和 π 模拓扑不变量的差值;灰色虚线和橙色虚线分别代表左右两边零模拓扑不变量的差值和 π 模拓扑不变量的差值;蓝色点代表图8 选取的参数.参数选 择: =9π/16,=π/4,=3π/4,以 及γ=0.2746[17]Fig.7.Black solid line represents quasienergy spectrum.Red solid line and blue solid line represents zero-mode and π-mode topological invariant difference,respectively.Grey dashed line and orange dashed line represents zero-mode and π -mode topological invariant difference,respectively.The blue dot indicates the parameter for Fig.8.Parameters:=9π/16,=π/4,=3π/4,and γ =0.2746 [17].

4.4 实验探测边缘态

前面几节已经在理论上验证了非布洛赫拓扑数与非厄米系统中边缘态的对应关系,但是如何在实验上探测非厄米系统中的边缘态依然是一个具有挑战性的问题.由于非厄米趋肤效应的存在,边缘态的波函数分布和体态波函数一样,都是局域在边界上,因此很难通过直接测量波函数在实空间分布的方法识别出拓扑边缘态.为了克服这一困难,我们通过对每一步时间演化的波函数加权求和的方法直接将边缘态模式提取出来.具体方法如下.首先定义

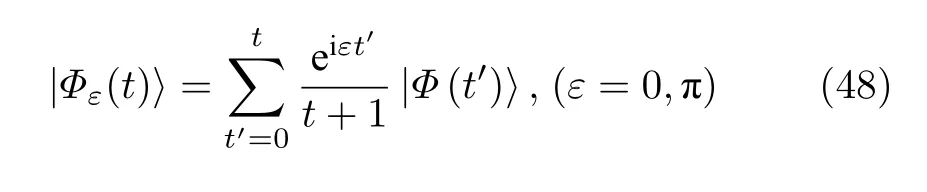
然后,把含时演化的波函数在本征态上做展开,得到

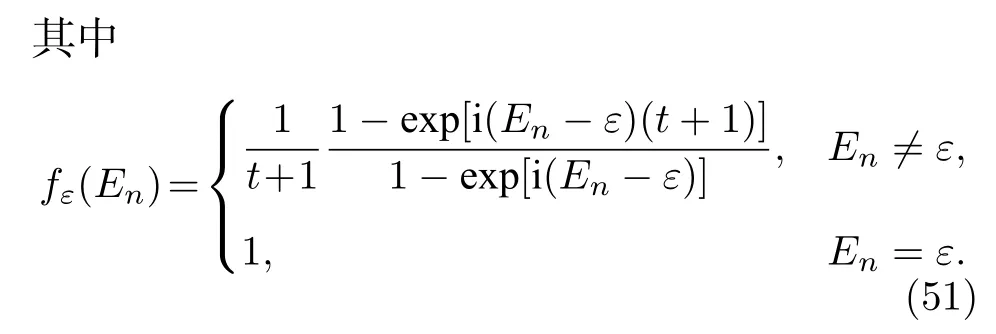
如果准能量能谱为纯实数时,那么对于Enε的本征态,其加权系数也就是说只要时间演化足够长,加权求和的波函数|Φ0,π(t)〉中只会留下能量为En=0,π 的本征态,也就是0 模和 π 模的拓扑边缘态.需要注意的是,在非幺正量子行走系统中,准能量能谱不一定总是纯实数,所以需要选取准能量为纯实数的参数区间进行探测.

图8 给出了将该方法应用到实验上得到的观测结果.在拓扑不变量满足=(0,-1) 的参数点,对于不同的初态选取,实验上都探测到了Φπ,+(x)的模式,并且其他模式占据很小.图8(d)—(f)中也将观测所得到的Φπ,+(x) 与实空间数值对角化得到的边缘态模式波函数做了对比.由两者相符可以看出Φπ,+(x) 的确提取到了ε=π 的本征边缘态模式.在实验上观测得到的拓扑边缘态与非布洛赫拓扑不变量一致,这也再一次印证了基于广义布里渊区构建的非厄米拓扑体边对应关系.

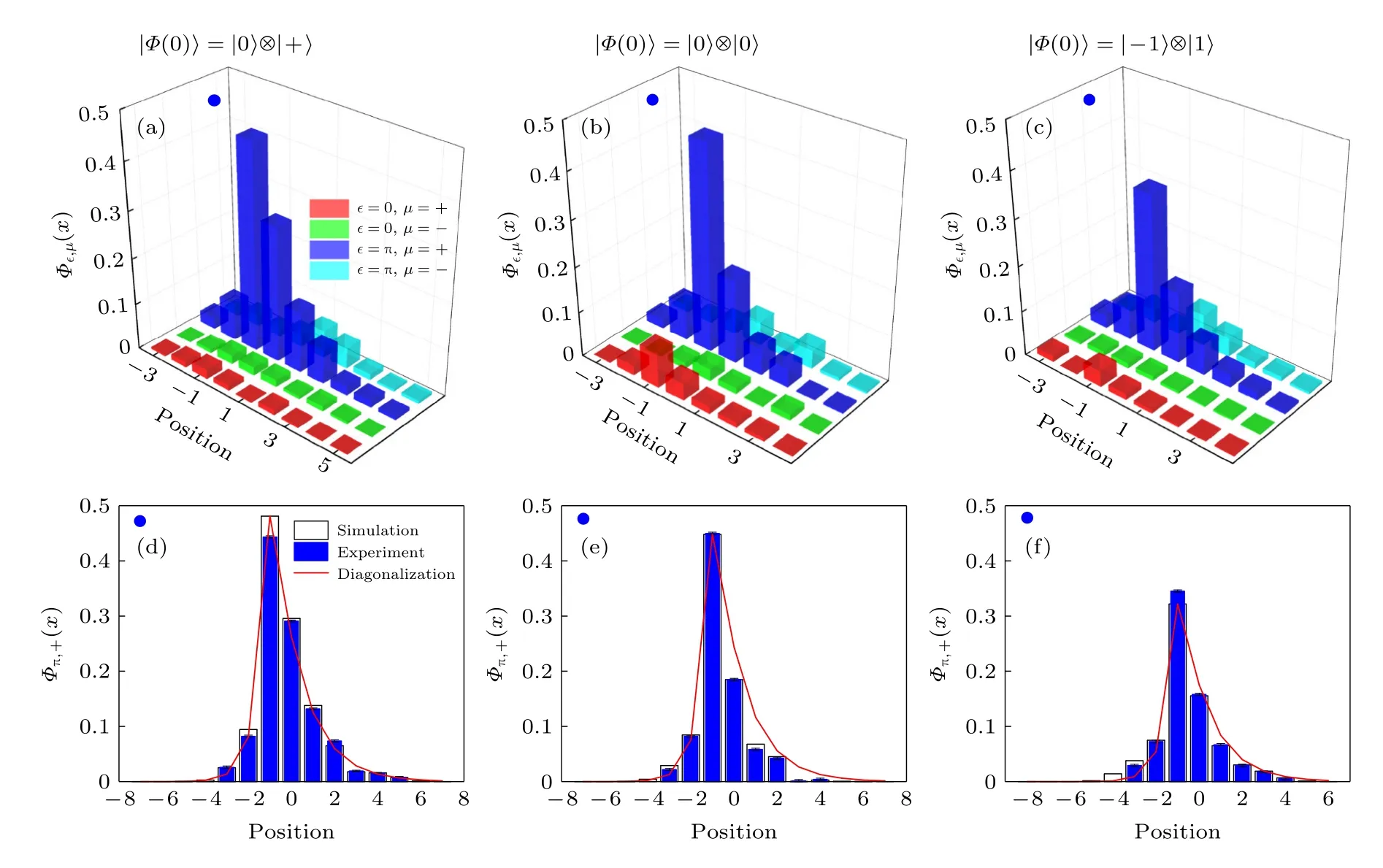
图8 (a)—(c) 不同初态选择下,7 步演化之后实验测量得到的 Φ ε,µ(x) ; (d)—(f) 数值模拟得到 Φ π,+(x) 和实验结果的对比.图中还给出了数值对角化 N =15 的畴壁系统对峰值进行缩放之后的结果.对角化得到的边缘态进行缩放的比例通过拟合Φπ,+(x)的中心峰值得到.其他参数与图7 相同[17]Fig.8.(a)—(c) Experimentally measured Φ ε,µ(x) after the seventh step with different initial states;(d)—(f) simulated Φ π,+(x) compared with experimental result.We also show the scaled norms of the edge state with ε =π by diagonalizing a domain-wall system with N =15 .Norms of the edge states from diagonalization are scaled to fit the central peak of the numerically-simulated Φ π,+(x) .Other parameters are as same as Fig.7[17].

5 总结与展望

本文主要介绍了畴壁边界条件下具有非厄米趋肤效应的系统中广义布里渊区方程的推导与求解,并由此出发讨论了非布洛赫能带理论在非厄米SSH 模型和非幺正一维量子行走实验模型中的应用.基于广义布里渊区计算的非布洛赫拓扑数可以正确预测畴壁系统中的拓扑边缘态,这印证了非布洛赫能带理论在不同边界条件下非厄米系统中的有效性.在不同模型中,畴壁边界条件下的广义布里渊区方程有一个统一的方程形式,对该方程背后物理内涵的充分理解,或许可以帮助我们找到一个对多种边界条件都普适的广义布里渊区方程.此外,不同边界条件下的高维系统中,广义布里渊区的计算分析也尚未被充分讨论,有待于日后进一步探索.