伸缩臂结构超级单元建模及失稳荷载快速搜索方法

2022-07-26卓英鹏，齐朝晖*，王刚，徐金帅，赵天骄

大连理工大学学报 2022年4期

卓英鹏，齐朝晖*，王刚，徐金帅，赵天骄

( 1.大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116024；2.大连理工大学海洋科学与技术学院，辽宁盘锦 124221 )

0 引言

流动式起重机因其灵活机动性强、伸展范围大，广泛应用在工程机械各领域，其中伸缩臂结构作为其主要的承载部件，起着不可替代的作用[1-3]．起重机实际工作时的荷载高度可达到几十米甚至上百米，伸缩臂展开后的结构通常都是细长形的，具有明显的几何非线性效应，此外，结构的稳定性也是限制起重性能的主要因素．

伸缩臂结构分析方面已经积累了大量的相关研究[4-7]，这些研究在一定程度上解决了很多理论和工程实际问题，其中相当部分的工作是直接采用商业软件中壳单元完成整个结构的有限元建模，而庞大的自由度和复杂的接触约束往往严重影响计算效率和收敛性．现有的很多文献、规范[8-13]中将伸缩臂视为变截面阶梯柱，采用能量法、瑞利-利兹法、精确有限元法等求解其变形、失稳等情况，实质上仍停留在截面变化的单个构件问题上，由多个截面厚度变化的空心单体组成的多结构复杂伸缩臂问题鲜有研究．而且，这种等效阶梯梁模型采用的是工程上常见的重叠部分抗弯抗扭模量叠加的方法，无疑会在重叠部分产生虚假的约束反力．

工程中承载后的细长结构整体表现为大变形，但局部区域内仍处于小变形范畴，结合这一特点，很多专家学者提出相应的几何非线性计算方法[14-15]，共旋坐标法[16]相对于早期参考初始构型的TL列式、参考当前构型的UL列式[17-19]等呈现出简单、高效的优势：可以应用现有的线性单元，省去复杂非线性单元的构造，深受工程设计人员的青睐[20-22]．

传统起重机臂架结构稳定性分析常采用的特征值屈曲分析方法适用于发生屈曲时仍处于线性变形状态的工况．对于重载条件下大变形失稳问题，追踪结构位移-荷载曲线平衡路径成为近代非线性稳定性理论发展的主要方向[23]，包括增量法、弧长法及改进的弧长法等各种方法[24-27]应运而生．这些方法在工程实践中被广泛应用，针对不同的具体问题，体现出不同的优缺点，但是均面临在保证精度前提下如何调整步长的困惑．

伸缩臂结构具有组合规则、计算工况多的特点，往往需要大批量性能计算，因此，很值得研究的问题是：能否在准确描述变形几何非线性效应及臂节间嵌套约束关系的前提下，尽可能减少自由度规模，快速地搜索结构的失稳荷载．鉴于此，本文提出一种可以满足上述要求的伸缩臂结构的超级单元建模及快速搜索失稳荷载的方法：采用梁单元对各臂节进行离散，以相邻臂节间接触截面节点、油缸铰接面节点作为边界点建立子结构；子结构内部节点自由度可通过内部平衡方程由边界节点自由度表示，进而转换为形式上两节点超级单元；以超级单元节点自由度作为系统变量，建立含荷载参数的结构非线性平衡方程及相应的切线刚度阵；最后采用平衡方程的微分形式快速求解结构的变形平衡路径及失稳荷载．

1 变截面臂节的梁单元拼接方法

组成伸缩臂结构的臂节长度尺寸远大于截面尺寸，是典型的空心细长结构，因此，臂节可采用常见的梁单元建模．梁单元的变形虚功率

(1)

其中，单元节点参数可表示为

(2)

(3)

图1 同一臂节中臂厚不同的截面Fig.1 The change of cross-section in the same boom segment with different thickness

(4)

其中

(5)

节点不在形心处梁单元变形虚功率和重力虚功率

(6)

其中

(7)

(8)

通过选择合适的截面特征点作为节点，建立截面形心和节点间的位移协调条件，实现变截面臂节各梁单元的拼接．

2 子结构单元位移分解及自由度凝聚

针对细长结构的几何非线性问题，最早由Wempner[28]和Belytschko等[29]分别提出的共旋坐标法将单元的位移场分解为随单元坐标系的刚体转动以及相对于单元的小位移．这类单元在具体应用中也体现出明显的优势[15]．但另一方面它与传统方法是一样的，如果要做非线性分析，结构中所有单元都要按非线性单元处理，最终导致结构平衡方程是一组维数很高的非线性方程．事实上，根据伸缩臂结构的特点，每个臂节可以合理地划分若干子结构，几何非线性效应主要体现在子结构连体坐标系大位移大转动上，子结构内部各节点相对于连体坐标系的位移转动可按小位移小转动处理．

图2所示的子结构由n个梁单元组成，将梁截面坐标系原点作为广义梁单元的节点，其相对于总体坐标系的矢径分别为r0，r1，…，rn，总体转动参数(卡尔丹角)为θ0，θ1，…，θn．R0，R1，…，Rn分别为截面瞬时方位矩阵，Ri(i=0，1，…，n)的列向量可由总体转动参数θi中各元素αi、βi、γi表示为

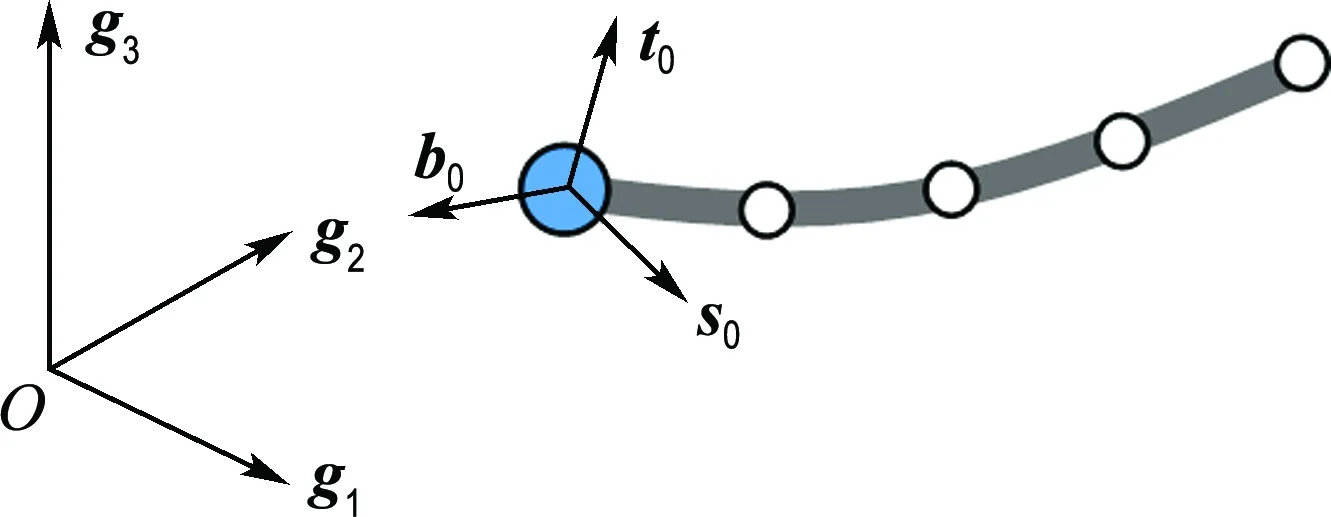
图2 子结构内梁单元Fig.2 Beam elements in the substructures

(9)

其中

(10)

定义子结构最左侧截面坐标系{t0，b0，s0}为子结构连体坐标系，子结构内任意一点的矢径

(11)

及其变化率

(12)

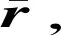
(13)

(14)

子结构内部任意一点的总体自由度虚速度分解为子结构连体坐标系的平动转动自由度和当前连体坐标系的局部自由度虚速度．由于连体坐标系中的局部自由度和总体坐标系下的总体自由度不一致，为将虚功率方程转化为代数方程，需要给出总体自由度和局部自由度之间的函数关系．梁单元节点在子结构连体坐标系下的位移可表示为

(15)

它的变化率

(16)

(17)

它的变化率

(18)

其中ωi是截面坐标系转动的角速度，它与总体转动参数θi中各元素αi、βi、γi转换关系为

(19)

最左侧截面节点位移转角相对于子结构连体坐标系为零，在子结构连体坐标系内描述的所有节点位移转角均为小位移小转角，满足线性梁单元的特征，且每个子结构中的节点可分为两类：(1)与其他子结构连接的边界节点集nb；(2)内部节点集ni．因此，可将子结构内部自由度凝聚到边界自由度上．

子结构坐标系下，对组成子结构的每个梁单元进行刚度阵组装并按内部节点自由度和边界节点自由度进行分块：

(20)

对应的变形虚功率

(21)

(22)

体力虚功率

(23)

式中：fg为子结构内任意一点的重力线密度；F0、T0是体力等效节点力相对于连体坐标系原点的合力和合力矩，表示为

(24)

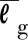
(25)

从中可得

(26)

臂节被划分为多个子结构后，臂节大位移大转动可以描述为子结构坐标系的大位移大转动，子结构内部的梁单元相对于子结构坐标系的变形属于小变形，因此可以认为单元节点在子结构坐标系下的位移和转动为小量．在此条件下，子结构刚度阵中元素为常量，因而

(27)

将式(26)、(27)代入式(21)中可得

(28)

体力虚功率

(29)

其中关联矩阵

(30)

等效刚度阵、等效重力影响系数分别表示为

(31)

这样，由n个梁单元拼接组装的子结构就缩减成了用两端节点位移和转角表示所有节点自由度的超级广义梁单元．

3 伸缩臂子结构划分及并联约束处理

常见多物体结构由受约束的典型的局部刚性区域依次串联而成，可称之为串联连接；伸缩臂结构是由多个空心结构通过层层环绕嵌套而成的系统，伸缩臂结构中臂节与臂节的连接方式区别于传统多物体结构，工作状态时臂节沿轴向的滑移运动被约束，整个臂节均为可发生大变形的柔体，这种连接可称为并联式连接．如图3所示，伸缩臂各臂节间通过销轴销孔连接，它们虽然存在缝隙，但与臂节的截面相比十分微小，且各臂节抗弯模量在同一数量级，接触区域都局限在内层臂左端和外层臂右端很窄的区域内；每个臂节最多有4个截面受其他臂节的作用：连接销轴的左端面、与其外层臂右端面接触的截面、与其内层臂销接的销孔所在截面、与内层梁接触的右端面，这4个特殊截面节点可分别称之为左端节点、外接触点、内接触点、右端节点．根据伸缩臂的这一特点，以这4个节点作为边界点对每个臂节划分子结构，每一个子结构内部可继续划分多个梁单元．这样，具有m个臂节的复杂伸缩臂结构可由共含有6(4m-2)个节点自由度的3m-2个子结构进行几何非线性分析．

图3 伸缩臂系统子结构划分Fig.3 Substructure division of the telescopic boom system

图4 伸缩臂结构臂节间的约束关系Fig.4 Constraints between boom segments of telescopic boom structure

(32)

第二类约束关系中截面②、④间的滑块限制二者沿截面内主轴方向的相对平移以及绕面外法向的相对转动，具有多体系统理论中棱柱铰的特点，对应的约束方程可写为

(33)

依据式(33)，选择r2、α2、β2、γ2、r4为独立变量，α4、β4、γ4为非独立变量．由此，式(32)、(33)共同组成伸缩臂结构两两相邻内外层臂间约束方程．

4 附加结构约束关系及等效节点力

传统结构问题的边界条件通常是直接约束位移，对这类约束的处理方法已经十分成熟．对于流动式起重机的伸缩臂结构，最外层臂(基本臂)与转台间为销轴铰接，存在一个机构自由度；该自由度则由臂节变形和工作状态下固定长度的变幅油缸支撑共同决定．此外，臂节所受到的外力不仅包括自重以及荷载，还包括臂头、起升绳施加的附加外力．这些附加结构向臂节施加的外力不仅与结构上的外力作用点位移相关，而且和约束结构本身的运动有关．

4.1 基本臂边界约束条件

转台与基本臂铰接部分如图5所示．由于销轴位置受到很大集中力，该处会进行加强处理，与臂节左端面焊接．

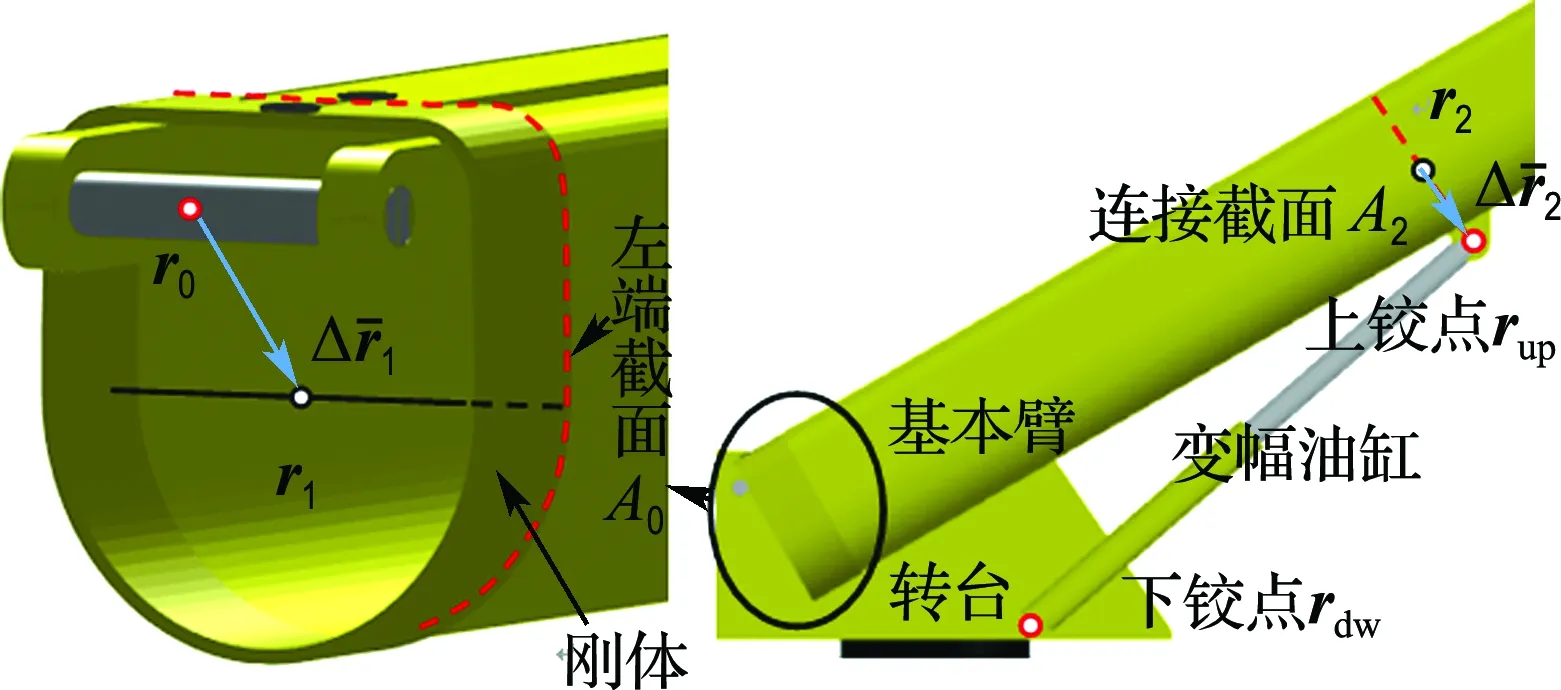
图5 基本臂与转台连接部分Fig.5 Connection between basic boom and turntable

左端截面A0的节点矢径r1与转动参数α1、β1、γ1存在约束关系：

(34)

其中r0为销轴中心点的矢径，选择初始状态转轴方向与销轴轴向重合的角度β1作为独立变量，剩余变量r1、α1、γ1为非独立变量，则R0可表示为

(35)

变幅油缸下铰点与转台铰接，上铰点与基本臂铰接．工作状态下，假设油缸长度保持恒定，本质上对上下铰点间形成固定距离约束．上铰点可由其所接触的截面A2的节点矢径r2和转动参数α2、β2、γ2表示为

(36)

其中R2为截面坐标系基矢量组成的矩阵．变幅油缸对基本臂的约束关系为

(37)

式中：d为油缸的长度，选择节点r2第一个分量作为独立变量，截面A2的其余描述参数为非独立变量．

4.2 臂头、荷载、起升绳附加节点力

流动式起重机伸缩臂臂头焊接安装在最内层臂的右端面上，如图6所示．起升绳一端连接于转台的卷扬上，另一端相切于导向轮表面．

图6 臂头与起升绳连接部分Fig.6 Connection between boom head and rope

臂头所连的最内层臂截面节点用D表示，将臂头视为质量为m的刚体，臂头的质心、起升绳作用点和荷载作用点在与臂头相连的截面坐标系Rn中的矢径分别为rm、rg、rp．则臂头质量和荷载对节点D处附加等效节点力可分别表示为

Tm=(mg(Rnrm)×mg)

(38)

(39)

起升绳绕过导向轮后，与n倍率起升滑轮组相连，绳索拉力大小为荷载G的1/n；工作状态下的方向与节点位移有关，可表示为

(40)

转换为节点D处附加等效节点力

Tn=(Gn/nRnrp×Gn/n)

(41)

5 结构平衡方程及切线刚度阵

以各臂节凝聚后的子结构边界节点自由度作为系统变量，将其按平动和转动划分，伸缩臂结构整体虚功率方程可以表达为

(42)

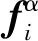
(43)

(44)

(45)

(46)

其中

(47)

(48)

子结构k的等效节点力和力矩对应的虚功率方程可改写为

(49)

定义系统描述变量q，结合式(42)和(49)，伸缩臂结构的整体虚功率方程可表示为

(50)

不失一般性，结构的约束方程可表示为

g(q)=0

(51)

根据相邻臂节间约束关系和边界条件，系统变量划分为非独立和独立两部分：

q=(qdpqip)

(52)

式(51)所派生的变分约束方程可表示为

(53)

非独立部分虚变分可由独立部分表示，存在关系

(54)

因而，由虚功率方程(50)可得用于求解的代数方程

(55)

此时，方程的个数与独立变量个数相同，需要添加与非独立变量相同个数的独立方程才可满足求解完备性，将平衡方程(55)与约束方程(51)相结合，可得到求解节点整体参数所需的方程：

(56)

这是一组高度非线性的方程，给出相应的切线刚度阵可大幅度提高求解效率．

为获得平衡方程的切线刚度阵，需要给出方程(55)的微分形式：

(57)

式子第1项中

Jfq=∂f/∂q

(58)

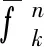
(59)

(60)

(61)

节点局部参数与总体参数的微分之间的关系可由式(45)、(46)得到，即

(62)

(63)

式子第2项需要将广义力f代入整体分析：

(64)

其中fdp为广义力阵f中独立自由度对应的子矩阵．补充的约束方程对应的微分形式可由式(53)得到，即

dg=Gdpdqdp+Gipdqip≜Gdq

(65)

将式(58)～(64)代入式(57)，结合式(65)，可得所需的切线刚度阵．

6 结构非线性平衡方程的微分形式

伸缩臂结构的变形求解方程是一组高度非线性方程，初值的选取严重影响迭代结果的收敛性．荷载是造成节点位移变化的主要参量，通过跟踪伸缩臂结构在不同荷载下的平衡路径可以快速求得任意荷载对应的变形以及最终的失稳荷载．整体伸缩臂结构的平衡方程可写作以下形式：

R(q)+λG0=0

(66)

式中：q是结构的节点位移和转角组成的列阵；荷载G按照某种比例施加在结构上，可表示为一个单位荷载增量G0和一个荷载控制参数λ的形式，即G=λG0．

传统荷载增量法将施加荷载分多个荷载步逐级增加，以前一步的计算结果作为当前步的方程初值，大大改善收敛程度，进而来追踪平衡路径．但是这种方法需要人为设置一个固定的荷载增量，该固定增量设置太小增加计算量，降低计算效率，太大又可能收敛失败，而且由于事先无法准确判断失稳荷载所在区间，太大的荷载增量很有可能直接越过极值点，导致搜索失稳荷载失败．

鉴于此，本文考虑将伸缩臂结构平衡方程对荷载控制参数求导，转化为微分方程，借助常规微分方程求解器中自动调节步长的优势，实现根据系统当前荷载状态对应的非线性程度自动调节荷载步大小的功能，在保证每一步求解收敛的前提下，快速追踪平衡路径和搜索失稳荷载．其主要操作如下：

(1)结构平衡方程(66)对荷载控制参数λ求导，得到微分方程

(67)

式中：(∂R/∂q)为平衡方程的切线刚度阵，∂q/∂λ反映当前荷载下位移-荷载曲线的非线性程度．

(2)依据平衡方程(66)，计算空载(λ=0)对应的位移转角q0，作为微分方程求解的初值．

(3)给定荷载控制系数上限λmax，在区间λ∈(0，λmax)积分微分方程(67)，积分过程中：(i)每一步用平衡方程(66)修正积分变量；(ii)时刻检查终止条件(5)．

(4)触发终止条件(5)，计算终止，得到失稳荷载以及加载至失稳荷载的平衡路径；没有触发终止条件(5)，计算至λmax，得到荷载上限Gmax=λmaxG0以及加载至荷载上限的平衡路径．

(5)如果系统遇到极值点失稳，求解微分方程的方法无法越过极值点，数值表现为位移对荷载系数的导数趋于无穷大，因此可设置

(68)

来判断结构是否失稳，其中ε为给定的阈值，代表位移-荷载控制参数值变化的倍数，可根据具体情况设定，当微分求解过程中位移对荷载控制参数的导数值变化倍数达到给定阈值时，此时对应的荷载就是结构的失稳荷载．

上述方法借助常规微分求解器自动调节步长的优势，可以在初始荷载增加阶段(线性变形阶段)以较大步长快速求解；同时在接近失稳阶段，迅速自动调节以较小步长逐步逼近失稳荷载．伸缩臂的综合性能由失稳荷载和强度破坏荷载共同决定，但失稳荷载的搜索为破坏荷载计算的前提，前者为后者提供了大量数据，因此在此基础上也可进一步完成对破坏荷载的计算搜索．

7 数值算例

图7所示为由弹性模量2.1×1011Pa、泊松比0.3、密度7 850 kg/m3的7节U形截面臂节相互嵌套组成的流动式起重机伸缩臂结构；臂节长度为L，每个臂节含1个销轴、4个销孔(从左至右，销孔号依次为1、2、3、4)，它们沿臂节长度位置分别记为L0、L1、L2、L3、L4；下盖板在长度位置为Ls处厚度发生变化，变化量为Δt；截面形式采用本文提到的由规则形状的圆弧组成的非规则复杂截面；各臂节具体相关尺寸见表1、2．基本臂左端面固连的转轴销接于回转平台，通过变幅油缸的支撑实现变幅．

图7 流动式起重机伸缩臂结构Fig.7 The telescopic boom structure for mobile crane

表1 臂节长度、销轴销孔位置、下盖板厚度变化位置和变化量(单位：mm)Tab.1 Boom segment length, position of pin shaft and hole, position and change of thickness of lower cover plate (units: mm)

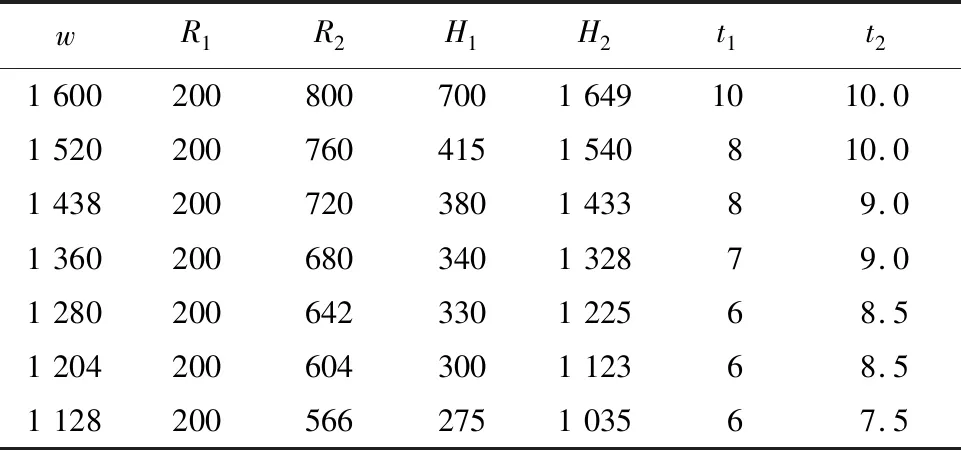
表2 臂节的截面尺寸(单位：mm)Tab.2 Cross-sectional size of boom segment (units: mm)

7.1 臂节子结构划分

以臂节间滑块相互接触截面节点、变幅油缸铰接截面节点作为边界点，沿长度方向将各臂节划分为如图8所示的子结构，其中3号节点为油缸连接截面节点，最内层臂划分为2个子结构，其余臂均为3个子结构，7节臂共需27个节点、20个子结构超级单元即可划分完毕．

图8 伸缩臂子结构单元划分Fig.8 Element division of the telescopic boom substructures

7.2 不同工况下伸缩臂结构的变形

针对图7所示的伸缩臂结构，应用本文方法得到了不同工况下的变形结果．具体的工况选择如表3所示，其中θ为初始状态下变幅角，k1、k2、k3、k4、k5、k6分别为由外层至内层1～6节臂相邻内层臂左端销轴依次插入的销孔号．

表3 计算工况Tab.3 Calculated working condition

(a) 工况1

由图9可看出：相同工况下，随着荷载的增大，伸缩臂的几何非线性效应逐渐增大；变幅角增大后，结构的承压效果明显，相同荷载作用时，弯曲变形会明显减小．

方便对比，采用ANSYS商业软件的Shell181单元建立工况2、4、5对应的有限元模型，变幅油缸使用Link180，相邻臂节间滑块接触部分的自由度局部耦合．

表4、5分别列出了工况2、4、5在不同荷载作用时，利用本文方法计算得到的臂头导向轮轴中心在竖直方向的位移和计算时间，以及与ANSYS 壳单元建模分析结果的对比．由表中数据可见，本文方法得到的位移解与ANSYS解差别很小．同时，采用ANSYS壳单元建模时划分82 806个节点，82 279个单元，需要求解496 836个非线性方程；本文方法划分了27个节点，20个超级单元，需求解162个非线性方程，求解过程变步长的实现会节约线性变形阶段的求解时间．此外，只需表1、2所示的尺寸参数即可实现程序化建模，无须重复ANSYS中每次建模的过程，为流动式起重机起重性能大批量快速计算提供了可靠的模型．

表4 工况2、4、5不同荷载作用下的竖直位移Tab.4 The vertical displacements under different loads of conditions 2, 4, 5

表5 工况2、4、5不同荷载作用下的计算时间Tab.5 The calculation time under different loads of conditions 2, 4, 5

7.3 全伸状态下伸缩臂结构的失稳荷载

图10给出了参考点位移相对于荷载的变化曲线，其中u表示第7节臂最右端节点位移，v表示第4节臂最右端节点位移．从曲线可看出，当荷载较小时，竖直位移基本保持线性；当荷载接近失稳时，位移曲线明显变陡，且表现出明显的非线性；事实上追踪平衡路径时，当荷载增加到接近极值点时，步长增量会逐渐趋于无穷小，当荷载位移曲线的斜率达到某个值时，已经非常接近失稳荷载，继续往下计算会浪费大量的计算时间，实际工程中可综合计算效率和精度要求，调整ε．