邢莉娟, 李 卓

西安电子科技大学综合业务网国家重点实验室, 西安 710071

1 引言

在实际环境中, 量子计算机的量子态不是孤立的, 他会与外部环境发生相互作用, 破坏量子态间的相干性, 从而导致量子消相干现象. 量子纠错码(quantum error-correcting codes, QECCs) 不仅能保护存储的量子信息, 而且能够实现容错量子门运算、容错量子态制备以及容错量子测量, 使得量子信息处理在有噪声的环境中能够可靠运行.

量子纠错码可以由某些满足特定性质的经典线性码来构造. 经典循环码尤其是BCH 码由于具有良好的代数结构, 是经典编码理论中一个重要的子类. 因此, 用经典BCH 码来构造量子码也引起了人们极大的兴趣. 通过大量研究[1–6], 目前已提出了很多构造给定参数量子纠错码的方案. 但是, 现有方案中的量子码均具有一定约束性. 例如: 有限域的阶必须是奇素数的幂[7,8]; 构造时某些参数有限制[1,8]; 或者满足特定的表达式[3,9]. 因此, 我们需要对已有的量子BCH 码的研究方案进行进一步的扩展和补充[4–6].

针对上述问题, 本文给出了选取分圆陪集的一般性方法. 该方法证明了满足一定条件的分圆陪集处于某个固定的区间范围内, 并给出了在给定区间内的分圆陪集包含元素数量的充要条件, 降低了构造量子BCH 时选取分圆陪集的复杂度. 然后用Steane 构造和Hermitian 构造分别构造出了偶数阶的非本原非狭义量子BCH 码, 构造出的新量子码具有更广泛的参数范围, 进一步丰富了量子BCH 码的种类.

2 基础与定义

令Fq表示q阶有限域, 其中q为素数的幂. 码C= [n,k,d]q表示Fq上的线性码, 其中n表示码长,k表示维数,d表示最小汉明距离. 在本文中, 若n与q互素, 则令qm ≡1 modn成立的最小正整数m被称为q模n的乘法阶, 用m=ordn(q) 来表示.

定义1(Euclidean 内积)[10]: 对于有限域Fq上的向量x= (x0,x1,··· ,xn−1)∈Fnq和y=(y0,y1,··· ,yn−1)∈Fnq, 他们的Euclidean 内积定义为

性质1[10]: 有限域Fq上的分圆陪集满足以下性质:

(1) 分圆陪集的元素个数一定是q模n的乘法阶的因子, 即|C[i]|| ordn(q). 特别的我们有|C[1]| =ordn(q).

(2) 对于任意的分圆陪集, 当且仅当i ̸=jqzmodn时,C[i]̸=C[j].

循环码因为具有严谨的代数结构和循环特性, 被认为是一类重要的线性码. 在经典编码理论中, BCH码通常用其生成多项式g(x) 的根来表示.

定义6(经典BCH 码)[10]: 有限域Fq上的码长为n, 设计距离为δ的q元BCH 码C是一个循环码, 其生成多项式可表示为g(x)=lcm{M(b)(x),M(b+1)(x),··· ,M(b+δ−2)(x)}, 其中,M(i)(x) 表示索引为i的最小多项式. 码C的定义集合为

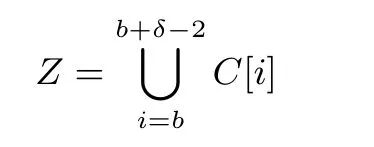
当n=qm −1 时, BCH 码是本原的; 当b=1 时, BCH 码是狭义的.

研究发现量子稳定子码可以通过经典线性码来构造. 目前, 量子码主要的构造方法包括CSS 构造、Steane 构造和Hermitian 构造.

根据上述定理, 只要能找到满足对偶包含关系的经典线性码, 就可以构造对应参数的量子码. 因此, 下面的引理给出了循环码是否满足对偶包含的条件.

引理1[2]: 若n与q互素, 即满足gcd(n,q)=1. 我们有下列结论:

(1) 对于Fq上码长为n的循环码C, 如果C的定义集合为Z, 那么C⊥E ⊆C的充要条件是Z ∩Z−1=∅, 其中Z−1={−zmodn|z ∈Z};

(2) 对于Fq2上码长为n的循环码D, 如果D的定义集合为Z, 那么D⊥H ⊆D的充要条件是Z ∩Z−q=∅, 其中Z−q={−qzmodn|z ∈Z};

通过定理1 和引理1可以看出, 构造量子稳定子码的关键是寻找满足上述条件的分圆陪集. 这些特定的分圆陪集不仅可以保证经典循环码是对偶包含的, 还便于计算该码的维数和最小距离.

3 有限域Fq 上的Steane 构造

在文献[1] 和文献[8] 中, La Guardia 给出了ordn(q) = 2 时, 码长分别为n=qm′−1 和n=r(q −1) 时的量子BCH 码的构造方法. 本文将q的乘法阶扩展至任意偶数阶ordn(q)=2m, 码长扩展至n=r(qm −1),r> 1. 然后研究码长为n=r(qm −1), 任意有限域Fq上偶数阶的量子BCH 码的构造方法.

3.1 m 为偶数

其中,iql+j ≥0.

综上, 假设不成立, 即Z ∩Z−1=∅, 码C满足Euclidean 对偶包含关系.

式(5) 和式(6) 相矛盾.

3.2 m 为奇数

4 有限域Fq2 上Hermitian 构造

4.1 m 为奇数

若m是奇数, 根据引理5, 我们选择的分圆陪集直接满足Hermitian 对偶包含的条件.

推论2若i为任意正整数, 当r(qm −1)|i时,C[i]=−qC[i].

4.2 m 为偶数

若m为偶数, 根据引理5, 我们无法直接找到满足Hermitian 对偶包含的分圆陪集, 下述推论很好的解决了这一问题.

5 性能比较与结论

本文中, 我们分别使用Steane 构造和Hermitian 构造给出了任意有限域上偶数阶量子BCH 码的构造方法, 下面我们与现有的结果进行比较.

(1) Steane 构造结果分析:

表1 Steane 构造方法得到的量子BCH 码参数比较Table 1 Comparison of quantum BCH code parameters obtained by Steane construction method

文献[2,13] 中, 都采用Steane 构造方法来构造量子BCH 码. 我们的方法在相同码参数下, 构造出的量子BCH 码的最小距离下界更大, 码的性能更好. 表格1 给出了一些码参数的比较结果, 可以看到我们的方法找到的量子BCH 码的最小距离下界明显优于参考文献[2,13].

文献[8] 中, La Guardia 给出了n=r(q −1), ordn(q)=2 时, 某些特定域上量子BCH 码的构造方法. 本文, 我们将这一结论扩展至任意偶数阶ordn(q)=2m, 码长扩大至n=r(qm −1), 任意有限域上来构造量子BCH 码. 我们的方法可以构造出范围更广, 码长取值更多的量子BCH 码.

(2) Hermitian 构造结果分析:

文献[2] 中, Aly 等人用Hermitian 构造生成了本原量子BCH 码. 采用本文所述方法, 我们生成了非本原量子BCH 码. 文献[8] 中, G. G. L. Guardia 用Hermitian 构造生成了非二元本原量子BCH 码.采用本文所述方法, 我们生成的是非二元非本原量子BCH 码.

文献[3] 和文献[8] 中, 作者都给出了n=r(q2−1), ordn(q2)=2 时, 某些特定域上量子BCH 码的构造方法, 其中q只能取奇素数的幂. 本文, 我们将这一结论扩展至n=r(q2m −1), ordn(q2) = 2m时,任意有限域上来构造量子BCH 码, 其中q为任意素数的幂. 我们的方法可以构造出范围更广, 码长取值更多的量子BCH 码.

综上所述, 本文首先分析了满足Steane 构造和Hermitian 构造的分圆陪集包含元素个数的充要条件,然后将量子BCH 码的构造方法扩展到任意有限域的偶数阶上, 给出了非本原非狭义量子BCH 码的构造方法. 与已有的结果相比较: 我们的方法在选取参数时没有太多的限制, 构造的量子BCH 码的最小距离下界更大, 码的性能更好. 更重要的是, 我们的构造方法是基于任意有限域的, 可以得到其他方案无法生成的量子码, 极大的丰富了量子BCH 码类的内容.