基于核凸非负矩阵分解算法的故障检测方法
2022-07-12祝朋艳徐进学张学磊
祝朋艳 徐进学 张学磊
(大连海事大学船舶电气工程学院 辽宁 大连 116026)
Graph regularization constraints
0 引 言
随着工业生产过程控制系统内部联系越来越紧密,局部故障的发生往往影响整体的生产,造成较大的经济损失。而大量传感器以及智能仪器可随时得到大量反映生产过程运行状态的数据,通过分析采样数据的特征信息,可寻找到适当的故障检测方法。采样数据一般具有高维、非高斯分布和非线性的特点。故障检测主要包括降维和挖掘数据两部分内容。对非线性数据来说,从高维空间中寻找一个更容易学习的低维嵌入不再是一种简单的线性函数映射。核变换方法通过核变换将具有非线性结构的数据投影到一个核空间,在此空间中复杂的非线性数据可以实现线性化表示,从而进行降维[1],代表方法有核主成分分析(Kernel Principal Component Analysis,KPCA)[2]和核Fisher判别分析(Kernel Fisher Discrimination Analysis,KFDA)[3]。另外,故障检测领域中常用到的主元分析法(Principal Component Analysis,PCA)[4]、偏最小二乘法(Partial least-squares,PLS)[5]和独立主元分析法(Independent Components Analysis,ICA)[6]等多元统计方法可用于提取数据特征,其中ICA要求比较严苛不太适用于复杂的工业过程数据的处理。KPCA是核化后的PCA,能够对非线性数据进行维数约简,同时捕获数据集的全局信息得以保留大部分的样本特征,从而成为故障检测领域中一种常用的多元统计方法。而实际过程中无论是描述一组数据集还是一幅图像,都要选取其重要的局部特征加以分析,这些局部特征往往使得整个识别分析过程具有可解释性,增加识别准确率。非负矩阵分解法(Non-negative matrix factorization,NMF)具有降维和提取局部特征的优点。考虑到原始数据不一定满足非负的限制条件,多种NMF算法的变体应运而生,主要包括半非负矩阵分解法(Semi-NMF,SNMF)[7]、凸非负矩阵分解法(Convex-NMF,CNMF)[8]和凸包非负矩阵分解法(Convex-Hull NMF,CHNMF)[9]等。其中CHNMF选取数据集流形结构的极端点作为局部特征,使其不再受矩阵非负的条件约束,放宽了传统NMF算法的应用范围。另外,在局部信息的提取过程中,一般希望能够尽量保持数据固有的几何结构不发生改变,即数据集的大部分信息不随矩阵分解过程而丢失。流行学习方法[10]广泛应用于故障检测领域,研究表明基于谱图理论的非线性流行学习方法[11]可以保持数据变换过程中局部近邻结构不发生改变。
通过分析核主元分析法(KPCA)与凸包非负矩阵分解方法的优势所在,本文提出了核凸非负矩阵分解(KCNMF)算法,并测试了其有效性。该方法首先将原始采样数据通过高斯核函数在高维空间中近似重构形成新的样本矩阵,并利用PCA对重构数据进行白化处理。然后利用凸包非负矩阵分解算法对白化处理后的数据矩阵进行分解,找到能表示数据集群整体信息的局部特征,而图正则化约束项则保证整个分解过程中数据分布的几何结构不发生改变。最后利用分解得到的基矩阵建立N2和SPE统计量,求得控制限,在与控制限数值的对比中完成对测试数据的故障检测。
1 核主元分析法
1.1 核主元分析法简介
假设有一样本矩阵Xm×n,有m个变量,而且每个变量有n个观测值。本文选取z-score标准化方法对数据进行无量纲处理。对序列x1,x2,…,xn进行变换:
(1)

原始输入空间中标准化后的样本xk经非线性映射Φ:Rm→F,在高维特征空间F中重构表示为φ(xk)∈F。那么在空间F中φ(xk)的协方差矩阵为:
(2)
进一步在特征空间中执行PCA:
SFp=λsp
(3)
式中:λ为特征值;p是与λ相对应的特征向量。将特征值按以下顺序排列λ1≥λ2≥…≥λn,取前d个特征值对应的特征向量作为PCA的主元方向。结合式(2)和式(3)得到:
(4)

在式(3)两边左乘映射向量φ(xk),形式如下:
〈φ(xk),SFp〉=λ〈φ(xk),p〉
(5)
联合式(4)和式(5),化简得到:
K2α=λsnKα
(6)
式中:K为核矩阵,(K)ij=k(xi,xj)=〈φ(xi),φ(xj)〉。
Kα=λkα
(7)
式中:λk=nλs。式(7)特征值分解运算后得到矩阵K的特征值λk,且进行降序排列λk1≥λk2≥…≥λkd,用下式选择前q个最大特征值所对应的特征向量α1,α2,…,αq:
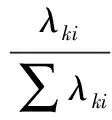
(8)
由此可计算特征空间中的特征向量P而得到主元方向。
1.2 特征空间数据白化
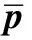
(9)
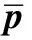
(10)
则白化后的样本矩阵为:
(11)

2 算法设计
非负矩阵分解(Non-negative matrix factorization,NMF)算法用于提取数据中“有意义的”部分变量,描述了数据集的局部特征。非负性要求使得该算法所关注的部分变量只会经过加运算去重构原始样本矩阵,特征之间不存在正负抵消的情况。用局部表现整体,分解过程简洁高效,分解结果具有可解释性是NMF算法的优点所在。
2.1 非负矩阵分解算法
设非负观测数据矩阵V∈Rm×n,其中行向量表示样本变量,列向量表示每个变量所包含的样本。NMF方法对非负观测数据V分解形式如下:
V=WHT+E
(12)
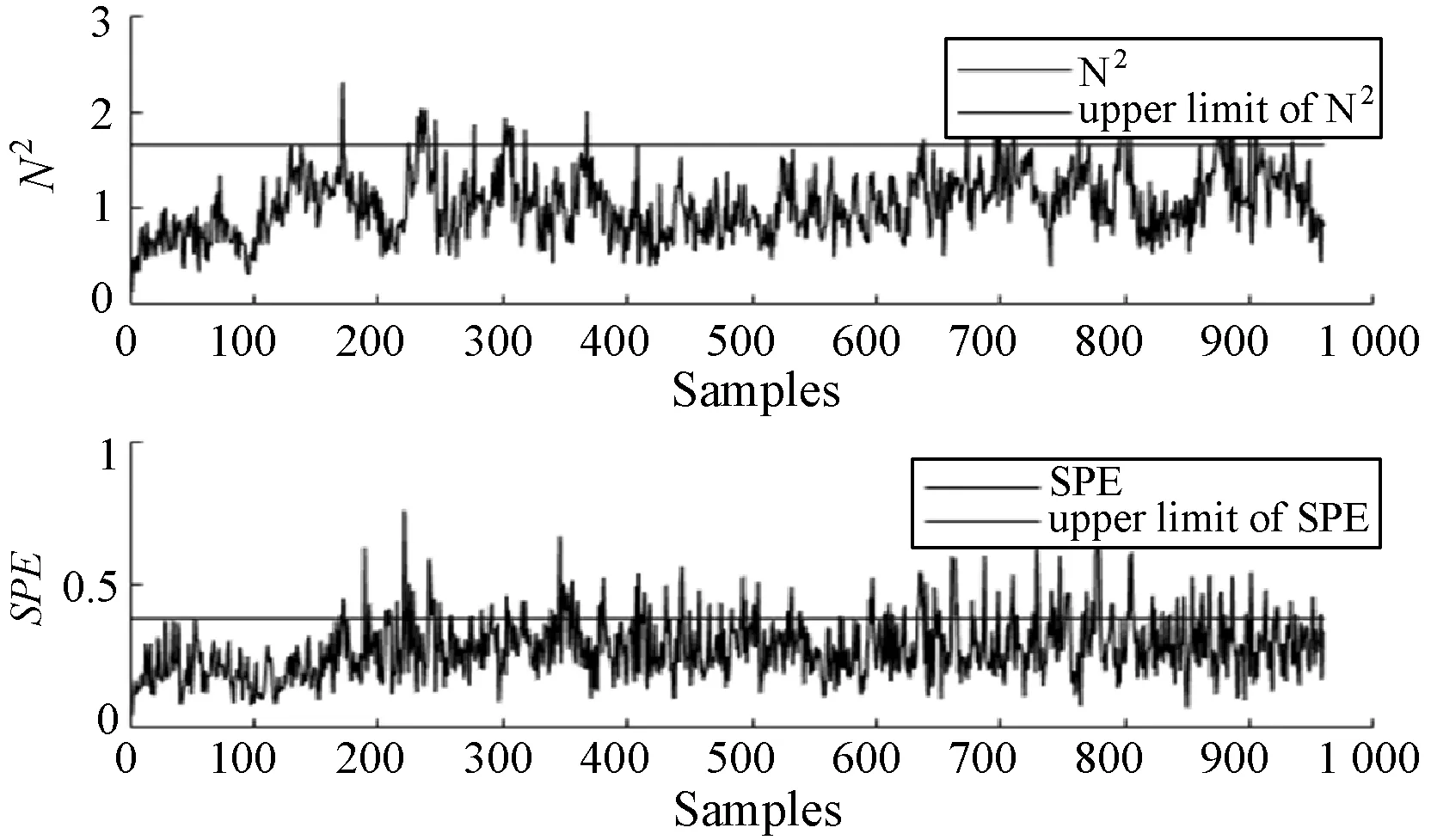
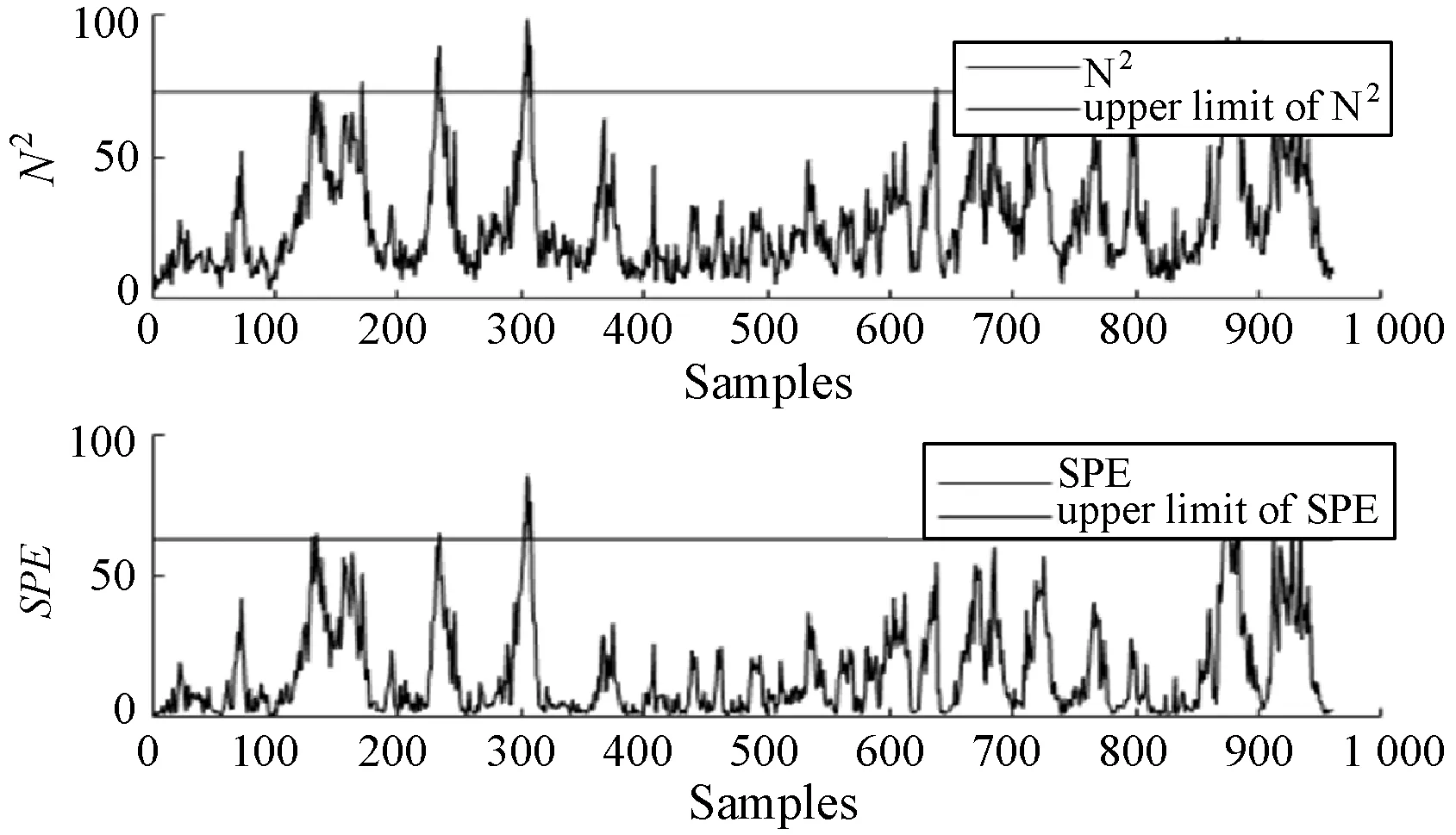
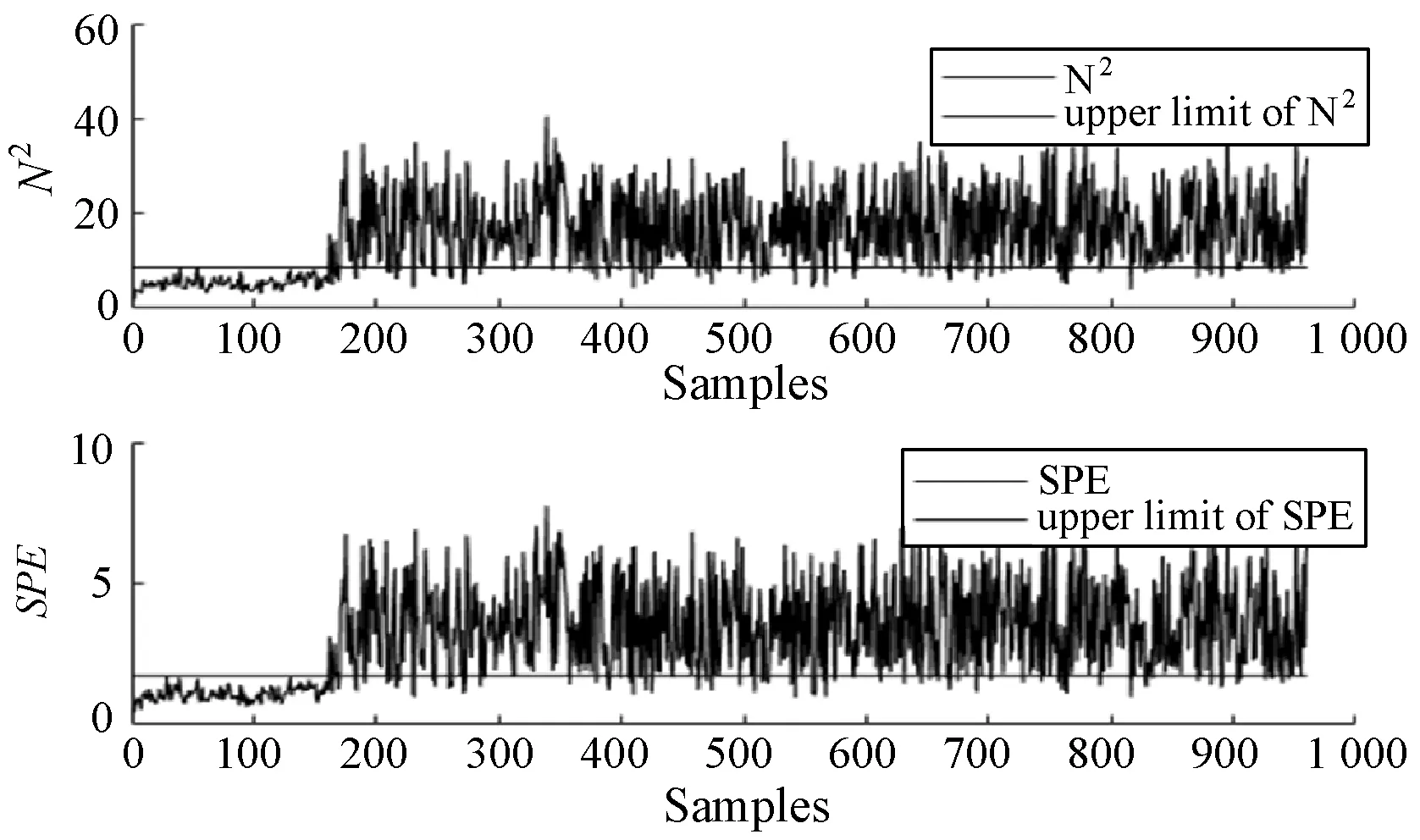
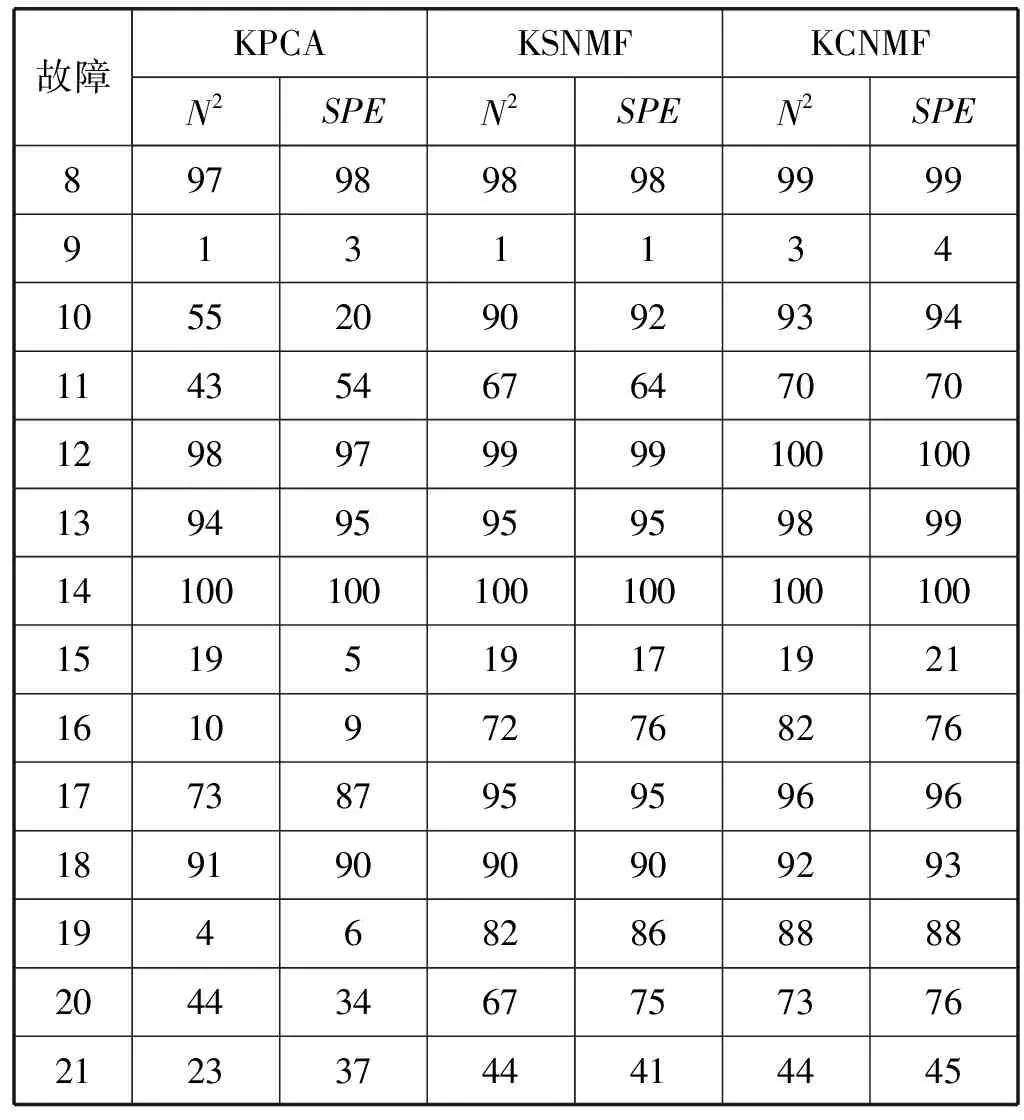
式中:W∈Rm×p表示基矩阵;H∈Rn×p称作系数矩阵;E∈Rm×n表示残差;参数p为近似描述分解之后的低维空间的维度。一般地,p NMF方法的求解是一个NP(Non-Deterministic Polynomial)问题,现有的方法都是将其归结为一个约束优化问题。最基本的优化函数为Lee等[13]提出的基于欧氏距离(F-范数)和广义Kullback-Leibler散度的优化模型。本文使用欧氏距离来度量矩阵V和两个分解因子W和H分解前后的误差大小: (13) s.t.W≥0,H≥0 对于W和H的求解遵循乘性更新法则,最终迭代形式如下[13]: (14) (15) 式(14)和式(15)在整个迭代过程中能够保证目标函数非增。目标函数达到收敛状态时,W和H便不再发生变化。 NMF算法提取数据局部特征,面对不完整的数据或者遇到局部噪声过大的情况,也不会对描述其他元素产生较大的影响,具有良好的稳定性和鲁棒性。其中,CNMF算法将原始的NMF算法从一个非凸问题改成凸问题,避免求解优化函数时得到局部最小值。不同于传统的NMF算法,CNMF并不需要损失部分数据信息。在凸非负矩阵分解算法中对基矩阵进行约束,使得基矩阵的列向量是某些原始数据点的加权求和,W表示有意义的“集群中心体”,具体表现形式为: (16) 则得到: V=WHT+E=VGHT+E (17) 凸包非负矩阵(Convex-Hull NMF,CHNMF)是CNMF框架中的一种,将CNMF的基矩阵W限制为凸包顶点集合Y。首先,CHNMF的局部特征由数据云团凸包顶点构成,顶点数总是少于数据集中数据的总个数,适用于大型数据集的分解。其次,很多研究中选取样本数据聚类中心为局部特征,聚类中心作为聚类样本均值往往代表着某类样本的一般属性。当正常样本与故障样本基本属性差别较大、中心位置距离较远时,聚类中心可作为检测的主要依据;反之,中心数据点作为局部特征具有较低的区分度,就需要获取更多的数据信息。CHNMF选取数据集流形结构的极端点(凸包顶点)作为局部特征,将聚类中心之外的边缘数据中蕴含的有效信息也考虑进去,进一步捕捉样本边缘特征,比较完整的系统信息有助于提高故障检测的准确率。最后,因为无须考虑聚类中心位置,CHNMF中W初始值设定不会对最终结果产生较大的影响。 令Y=VG,Y∈Rm×k表示V的凸包顶点的集合。通过在凸包上找到k个合适的数据点来求解下面优化函数的最小值: (18) s.t.yi∈v(V)i=1,2,…,k 若数据集过大,则凸包计算变得困难。对数据进行二次降维,用数据低维映射后的凸包顶点来代替原空间中的凸包顶点[8]。实质上,V中包含有限多的点在空间中形成一个多面体,由下面多面体定理可以得知,数据线性低维投影的凸包上的任何数据点也位于原始数据的凸包上。 多面体定理:在仿射映射π:x→Mx+t下的多面体P的每一幅图像都是多面体[14]。 FastMap映射[15]可以将样本矩阵线性投影到二维空间中得到新的样本矩阵S∈Rm×r,在二维空间中我们选择其中k个凸包顶点得到基矩阵Y。凸包顶点是特征数据点,而每一个特征数据点是所有数据点的一个凸组合,所以离特征数据点距离越近的点对特征点构成的影响就越大,对应着参数矩阵G∈Rr×k中的数值就会越大[16]。 V=YHT+E≈SGHT+E (19) 式中:H∈Rn×k为系数矩阵。 优化算法的目标函数是: (20) s.t.G≥0,H≥0 迭代更新规则如下[9]: (21) (22) 式中:S是由数据V进行FastMap投影后的数据集合。(STV)+=(|STV|+STV)/2,(STV)-=(|STV|-STV)/2,(STS)+=(|STS|+STS)/2,(STS)-=(|STS|-STS)/2分别表示数据矩阵的正数部分和负数部分。 将数据矩阵中的xi看作是图中的一个顶点,用G=(V,E)表示图,V={v1,v2,…,vn}是图的顶点集合,E={e1,e2,…,em}表示图中边的集合[17]。而两点之间的权重wij构成图的带权邻接矩阵W=(wij),i,j=1,2,…,n,由于G是无向图,令wij=wji。其中顶点vi∈V的度可以定义为:di=∑wij,度矩阵D是对角元素分别为度d1,d2,…,dn组成的对角矩阵。图的构建有几种不同的形式,本文选择全连通图的构建形式,顶点vi和vj之间的边的权重值由高斯相似度函数来计算得到: (23) 式中:参数σ控制相邻关系的宽度。由式(23)可知:当两数据点之间具有较近的物理距离时,二者之间的相似度较大,边的权重值越大;反之,权重值越小。图拉普拉斯矩阵L=D-W可用于表示包含度和边的权重值等必要元素的图。 数据映射之后,在新的基底下的数据表示形式为fk(xi)=hik。此时,数据点之间的近似程度计算如下[11]: (24) 由式(24)可以看出,原来距离较近的两个数据点在新的基底下同样能够保持较近的距离和较大的相似度。 本节提出一种基于核凸非负矩阵分解算法(KCNMF)的故障检测方法,主要用于解决非线性数据降维和样本矩阵局部特征提取的问题。 非负观测数据矩阵V∈Rm×n,其中行向量表示样本变量,列向量表示每个变量所包含的样本。对样本矩阵X进行白化处理得到KPCA空间中的样本矩阵Z,对Z进行CHNMF分解得到KCNMF模型的表达式如下: Z=SGHT+E (25) 式中:Z∈Rq×n为白化后的样本矩阵;S∈Rq×r为FastMap映射降维后的样本矩阵;G∈Rr×k为参数矩阵;H∈Rn×k表示系数矩阵;E∈Rq×n表示残差矩阵。 采用欧氏距离用于度量矩阵分解前后的近似程度,目标函数优化过程中增加流形正则化约束。非负矩阵分解算法希望提取出的基矩阵能够更好地近似于原数据矩阵。如果基向量能够反映数据本身固有的黎曼结构而不是欧几里得结构,数据的关键信息就可以通过几何结构的局部不变性得以保留下来。如果两个数据点zi和zj在数据分布的固有几何形状上相近,那么新的基底下的数据hi和hj也应该是相接近的[18]。结合式(24)和式(25)得到目标函数具体形式如下所示: (26) 式中:λ是常系数。 保持H不变,按下式更新G+: (27) 保持G不变,按下式更新H+: (28) N2=hTh=zT(SG)(SG)Tz=zTSGGTSTz (29) 而SPE统计量主要用来反映样本在残差空间中的投影变化,它表明数据样本与核凸非负矩阵分解模型的偏离程度,用偏差设定检测阈值也是一种重要的方法。 (30) 确定N2和SPE统计量之后,还需进一步求得监测统计量的控制限来判定样本是否处于故障状态。实际采样数据大多具有非高斯的特点,所以N2和SPE统计量的控制限就不能通过特定分布方法来确定,否则会造成较大的偏差。作为一种非参数估计方法,核密度估计法(KDE)[19]可用来估计过程数据的概率密度并提取数据分布信息,且不需要已知数据的先验知识和数据分布。具体形式如下: (31) 最后累积分布函数(CDF)用于计算N2和SPE统计量的控制限。 (32) 由此,在对测试数据进行状态分析时,如果新数据统计量处于控制限范围内可判定其属于正常状态,如果高于控制限则为故障状态。 实际工业生产过程是一个非线性系统,但是在某个工作点采样得到的过程数据可以近似成线性样本,假设生产过程是拟平稳过程。利用正常操作下的历史数据构建离线模型得到N2和SPE的故障检测阈值,新采样得到的在线数据根据在线检测流程计算得到新的N2和SPE统计量,用于判断是否在控制限范围之内从而说明数据是否故障。则故障检测过程如下所示: 1) 离线建模阶段过程如下: (1) 工业生产的正常操作之下采集传感器中的数据样本V∈Rm×n,利用一般的标准化方法对数据进行标准化处理; (4) 利用式(10)求得白化矩阵P,并用式(11)将样本矩阵进行白化求取新的样本数据Z; (5) 对白化后的新数据样本矩阵Z进行凸包非负矩阵分解,求得X和H; 2) 在线建模阶段过程如下: (1) 在线数据测试时需先获取新样本vnew∈Rm,因为是工业生产是拟平稳过程,使用训练样本的均值和方差对此新样本进行标准化操作; (3) 利用式(11)对vnew求特征空间白化后的样本znew; (4) 对白化后的新数据样本矩阵Z进行凸包非负矩阵分解,求得新的系数矩阵hnew; 本文中采用的实验数据来自于Tennessee Eastman(TE)仿真平台。TE过程的流程图如图1所示。 图1 TE过程的工作流程图 整个TE生产过程中,可采得含有52个变量的数据集。数据集可分为22个测试集和22个训练集。第0号测试数据集和训练数据集分别表示数据是在生产机器在正常状态下运行48小时和25小时采集到的,得到的样本数分别为960个和500个。第1-21号数据集是在21个不同故障模式下经过48小时运行仿真得到,在运行过程的第8个小时处分别引入不同类型的故障,每个数据集都采集960个样本,从160个样本之后都为故障样本。21个故障模式如表1所示。 表1 TE过程故障模式 续表1 对1-21种故障数据集进行检测时,其难易程度大致可分类如下[20]:检测较容易的有故障IDV(1-2)、IDV(4-8)、IDV(12-14)和IDV(17-18)。不太容易被检测的有IDV(10-11)、IDV(16)、IDV(19)和IDV(20-21)。非常难以被检测到的有IDV(3)、IDV(9)和IDV(15)。 选取相对比较有代表性的故障4、故障10和故障19作为实验对象来测试核凸非负矩阵分解算法的故障检测性能,以验证KCNMF对数据非线性的处理以及对局部特征的挖掘是有否有利于提高检测准确率。图2-图5分别是PCA、KPCA[21]、CHNMF和KCNMF四种方法对TE过程故障4的故障检测的结果。 图2 PCA方法的故障4检测结果 图3 KPCA方法的故障4检测结果 图4 CHNMF方法的故障4检测结果 图5 KCNMF方法的故障4检测结果 从仿真结果可以看出,KPCA的检测结果优于线性检测算法PCA,说明KPCA对于非线性故障数据的处理具有较好的效果。而KCNMF的检测准确率又优于KPCA。因为故障4是由反应器冷却水入口温度产生改变而造成流速和反应器中温度两个局部变量变化造成的,其他变量基本保持稳定,KCNMF方法可以很好地提取数据中的局部信息,提高了工业过程的故障检测性能。另外,KCNMF方法可以很好地应对数据中的非线性关系,所以检测效果比CHNMF方法更好。 故障10是物料C的温度发生了改变,但由于TE过程可以反馈这个变化,并且缓慢地消除了这个误差,使系统的温度尽可能调整到正常值。图6-图9分别为PCA、KPCA、CHNMF、KCNMF对故障10的检测结果。可以看出PCA和KPCA的N2和SPE统计量只能够检测出部分故障就是故障10的特点造成的。而CHNMF的检测结果优于上面两种方法,对于局部特征关注优势明显。不过,KCNMF方法的N2和SPE统计量还是比上述三种方法更胜一筹。 图6 PCA方法的故障10检测结果 图7 KPCA方法的故障10检测结果 图8 CHNMF方法的故障10检测结果 图9 KCNMF方法的故障10检测结果 图10-图13分别为PCA、KPCA、CHNMF和KCNMF方法对故障19的检测结果。通过表1可知,虽然故障19的故障类型未知,但根据检测结果可以推测出,故障19可能与局部变量发生变化有关。可以看出PCA、KPCA以及CHNMF算法的检测准确率普遍较低,而KCNMF方法因在数据非线性关系的处理以及局部特征的提取利用上面具有较大的优势,因此能够表现出较高的检测准确率。 图10 PCA方法的故障19检测结果 图11 KPCA方法的故障19检测结果 图12 CHNMF方法的故障19检测结果 图13 KCNMF方法的故障19检测结果 表2中列出了对1-21种TE过程非线性数据分别使用三种故障检测方法的检测准确率。其中核半非负矩阵分解算法(KSNMF)[22]提取的局部特征是数据云团的聚类中心。表中结果比较可得,KSNMF和KCNMF这两种方法的检测都明显优于KPCA,这说明对于数据云团局部信息的提取利用有助于故障数据的识别与检测。而KCNMF方法相较于KSNMF方法检测中结果表现更好,因为KCNMF将偏离聚类中心的数据信息也考虑进去,当不同样本聚类中心过于接近,以此为基础的局部特征不具备良好的区分度,则边缘数据所含信息对检测会起到重要作用。对分解结果产生很大影响。KCNMF不再需要设置聚类中心的初始值,避免了迭代初始值和低维阶次设定不准确导致检测结果存在误差的情况出现。总体来说,KCNMF对第一、二类故障数据整体检测效果较好,而第三类故障检测效果不佳,还需进一步研究。 表2 KPCA、KSNMF和KCNMF方法故障检测率比较 (%) 续表2 为解决高维非线性数据降维问题,并求取更有意义的样本矩阵局部特征,本文提出了核凸非负矩阵分解算法。首先对数据集进行核主元分析并对特征向量进行缩放求得白化矩阵,利用白化矩阵对样本方差进行缩小或放大操作。接下来,对白化后的样本矩阵进行凸包非负矩阵分解。用凸包顶点作为局部特征所求得的故障检测方法在关注数据集聚类中心之外,还充分利用了边缘数据信息,能捕捉到其他方法捕捉不到的特征。流行正则化约束项又能保证分解过程中样本矩阵的本质不发生改变,这些算法的结合使得故障检测更加准确。本文利用TE过程数据集对KCNMF方法进行仿真验证,取得了较好的诊断结果,并验证了所提方法的有效性。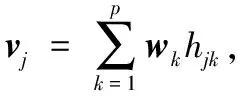
2.2 凸包非负矩阵分解算法
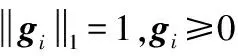

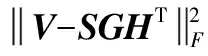
2.3 图的基本理论

3 核凸非负矩阵分解的故障检测方法
3.1 在KPCA空间进行凸包非负矩阵分解
3.2 故障检测统计量


3.3 基于核凸非负矩阵分解算法的故障检测过程
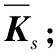
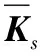
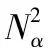
4 仿真分析
4.1 实验数据



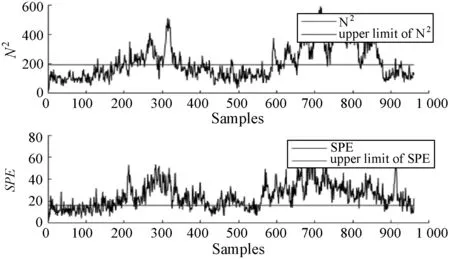
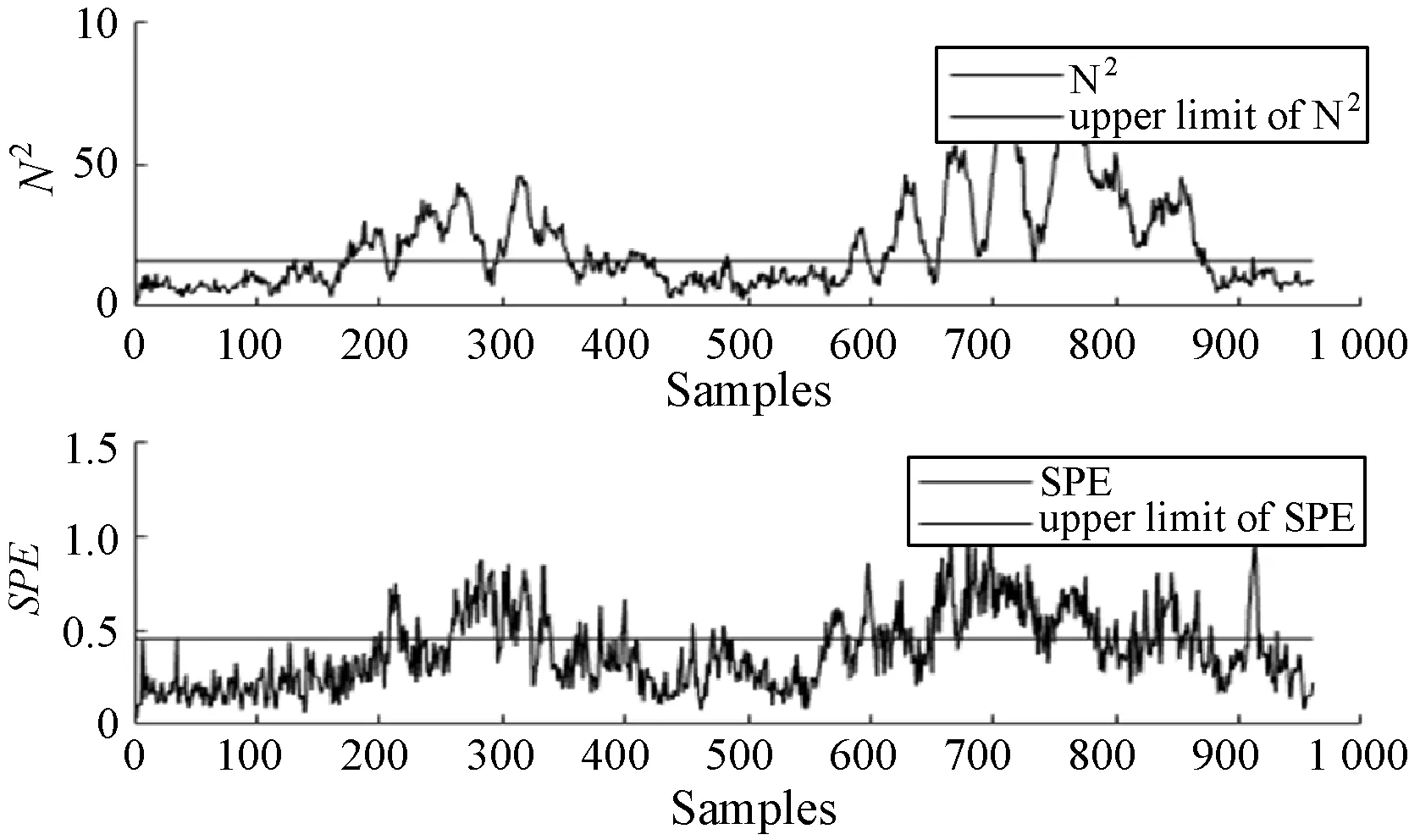
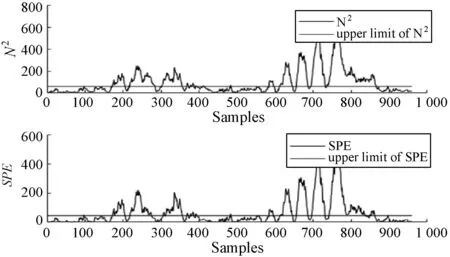
4.2 实验结果







5 结 语
