周月娥， 刘泰玉， 严鹏

(广西民族大学建筑工程学院， 南宁 530006)

箱型梁具有良好的结构性能，在工程中有着广泛的应用。箱型梁进行随机分析和可靠度分析在实践中需要考虑一些不确定因素。可以对箱型梁进行随机分析的方法有蒙特卡洛有限元法[1]、响应面法[2]和随机有限元等方法。蒙特卡洛有限元法在抽样模拟次数增加的条件下，计算结果接近实际解，因此常作为其它结构随机分析方法的比较基准。但是，需用大量的计算时间来获得一个有效的计算分析结果。响应面法分析时所需样本点少、计算量适中、与确定性结构分析解耦。然而，由于事先不可预知验算点，需要每次迭代得到样本点来保证响应面与真实极限状态曲面在验算点附近较为接近。摄动随机有限元法[3]不用样本实验和统计数据分析，对随机场的信息处理技术要求比较低，只需知道随机参数的前两阶矩就可以得到比较好的结果。现有的薄壁结构设计研究分析中可用的是一次二阶矩法[4]，对其进行可靠度计算的数值分析方法较少，在处理复杂问题时存在一些困难。考虑了工程中的不确定因素后，通过在标准正态空间中寻找最近原点，可以间接得到结构的可靠度指标[5]。寻找这个点的计算方法是一个不断迭代程序[6]，需要通过计算极限状态函数值和它在每一步相对于基本随机变量的梯度，求解梯度可以选择使用随机有限元法[7]或者有限差分法[8]。

现有的箱型梁确定性元分析中梁单元节点位移中都含有剪力滞函数[9-11]，并且没有考虑箱梁参数的随机性。文献[12-13]建立的箱型梁剪力滞效应分析方法中，用附加挠度及其一阶导数代替剪力滞函数，克服了采用剪力滞函数所建立方法的缺陷。为此，结合基于附加挠度建立的箱型梁有限元分析方法和摄动随机有限元法建立一种可以对箱梁结构求解可靠度指标的迭代求解方法，主要是通过处理可以寻找标准正态空间中离坐标原点最近点时极限状态函数对随机变量的梯度。选取原变量空间中的均值点为初始迭代点，分别基于验算点和均值点迭代求解极限状态函数的梯度，即可得到结构的可靠指标。通过两种方法对箱型梁进行分析，可以考虑参数随机性对箱梁可靠度计算的影响，也可以对比分析两种方法的适用范围。

1 箱型梁随机分析的摄动随机有限元法

图1、图2所示的左端固定右端自由的箱型梁，翼缘横截面的纵向位移函数u(x,y)由箱梁挠度w(x)和附加挠度wa(x)确定[12]。

图1 承受外荷载作用的箱型梁简图

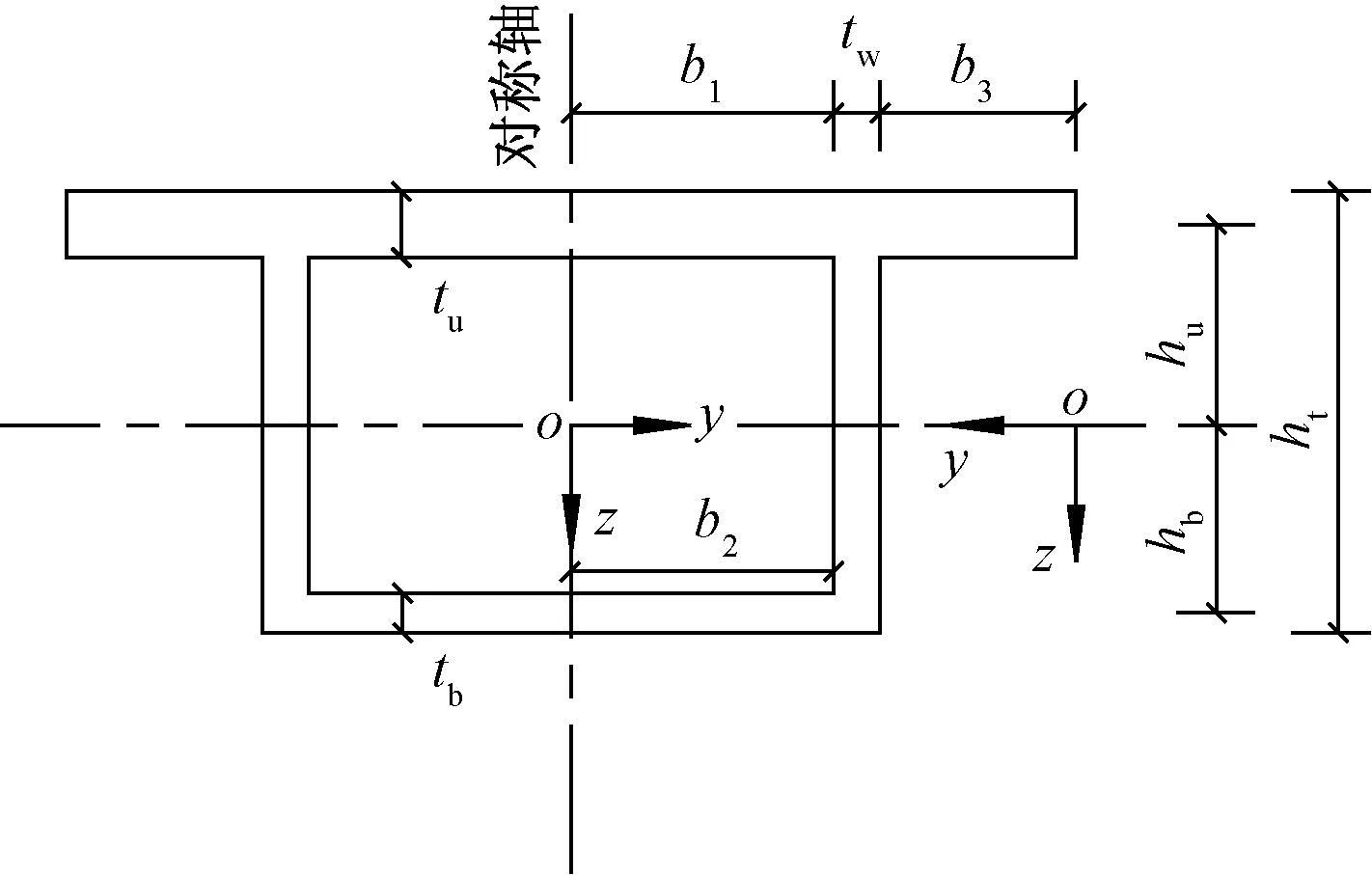
图2 箱型梁横截面尺寸

(1)

式(1)中：h为翼板到箱型梁截面形心的距离；b可取b1、b2和b3，分别为箱梁截面两腹板之间上、下翼板宽度1/2及悬出翼板的宽度；I为箱梁整个截面的模量；Is为箱梁上下翼板的模量,且有

I=Is+Iw

(2)

(3)

式(3)中：m2=b2/b1;m3=b3/b1。

在分布荷载q(x)作用下，利用式(1)定义的位移函数，建立箱梁的总势能泛函，可表示为[12]

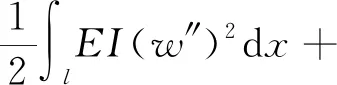
(4)

式(4)中：l为箱型梁的长度；E为弹性模量；G为剪切模量。

当箱型梁边界条件不同时,式(4)定义的箱型梁总势能泛函中有关挠度w(x)和附加挠度wa(x)的表达式是不同的。根据箱型梁的一维离散有限元法[13]，总势能泛函用矩阵形式表示为

(5)

式(5)中：

(6)

式(6)中:μ为材料的泊松比。

考虑材料和外荷载的随机性，式(5)中的D、T、Π、χ、d都为随机量，按照二阶泰勒级数展开为

(7)

(8)

(9)

(10)

(11)

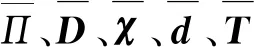
把式(7)～式(11)代入式(5)中，可得总势能泛函Π的二阶展式为

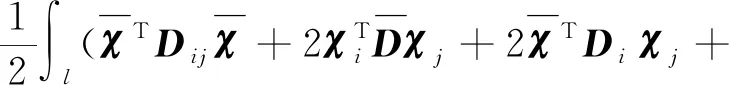
(12)

基于摄动随机变分原理[3]，直接得到总势能泛函二阶展开式的一阶变分，并考虑式(13)、式(14)。

(13)

(14)

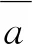
可得

(15)

(16)

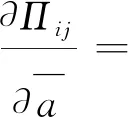
(17)

完成式 (15)～式(17)的整理分析的基础上，得到控制方程为

(18)

(19)

(20)

(21)

(22)

(23)

2 结构可靠指标及其梯度优化迭代算法

2.1 结构可靠指标

把对箱梁结构有影响的基本随机变量X作为自变量时，可得描述极限状态的功能函数Z为

Z=g(X)

(24)

结构的可靠指标为

(25)

2.2 结构可靠指标的求解

(26)

式(26)中：G为功能函数；min表示取最小值。

采用迭代公式[式(26)][5]计算验算点x(k+1)，其计算公式为

(27)

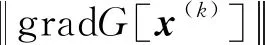
3 基于摄动随机有限元法的可靠指标求解

3.1 功能函数

用局部平均法[14]离散箱型梁随机场，得到随机变量X，其功能函数为

g(X)=u*-u(X)

(28)

式(28)中：u*对应于控制截面的最大容许挠度；u(X)为对应于箱梁正常使用极限状态的挠度响应。

3.2 功能函数的梯度

2.2节利用式(27)迭代寻找验算点的关键是确定梯度向量gradG(x)。一般这种情况下，原变量空间中的功能函数g(X)可以得到，求梯度向量gradG(x)可转化为求gradg(X)，可表示为

(29)

式(29)中：函数g(X)不能用随机变量显式表示，可表示为

g(X)=g(R,S)

(30)

式(30)中：R和S分别为结构抗力和作用效应。

则有

gradg(X)=JRgR+JSgS

(31)

式(31)中，gR、gS分别为函数g(X)对R和S的梯度向量；JR、JS分别为R、S的雅克比矩阵。

由式(31)可以看出，求出雅克比矩阵JR、JS及梯度向量gR、gS是关键问题。一般情况下，JR、gR和gS容易获得。由于结构的随机效应S不易用X显式表达，所以难以用解析法求解雅克比矩阵JS。

3.3 摄动随机有限元法求梯度向量

如3.1节所述，可以选取一个结点的位移a作为箱梁极限状态方程中控制截面的响应量。求解1节中控制方程，可以求得ai。雅克比矩阵JS第i行的转置是响应S的一阶偏导数，有

Si=ai，i=1,2,…,n

(32)

ai可根据式(18)、式(19)求得

(33)

即而可以确定JS为

JS=[ai]T,i=1,2,…,n

(34)

进而由式(31)求出梯度向量gradg(X)。

3.4 正态相关随机变量的处理

如果得到了相关正态随机变量X，需要把X转化为标准正态随机变量x。

首先，通过正交变换得到不相关的正态随机变量Y，可表示为

Y=ATX

=[Y1,Y2,…,Yn]T

(35)

式(35)中：A为与随机变量协方差矩阵CX的特征值λi(i=1,2,…,n)相应的n个正交规范化特征向量形成的矩阵。

然后，标准化Y，得到不相关的标准正态随机变量xi为

(36)

式(36)用矩阵表示为

(37)

式(37)中：T为特征值矩阵。

结合式(36)可得

(38)

将3.3节推导得到的gradg(X)和式(38)代入式(29)就可以得到标准正态随机变量空间中功能函数的梯度gradG(x)。然后，由式(27)可以用优化迭代算法得到验算点坐标，即而得到可靠指标。

3.5 简化迭代分析

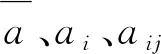
(39)

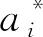
(40)

4 算例分析

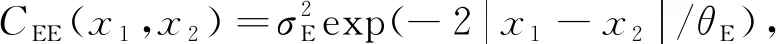
(41)

当箱型梁两端为固定端，分别取两种工况考虑箱梁的随机性，利用基于验算点的摄动随机有限元可靠度算法(计算结果标记为PSFEM1)及其简化迭代计算方法(计算结果标记为PSFEM2)计算在不同变异系数情况下箱型梁的可靠指标。以蒙特卡洛有限元法(计算结果标记为MCS)可靠度计算结果为基准，分析PSFEM1和PSFEM2的误差。

从图3可以看出，在不同变异系数下，PSFEM1和PSFEM2的计算结果比较相近，两者之间误差在工况一和工况二情况下分别不超过1.83%和0.48%，与文献[15]结论较为一致。可以看出，当变异系数增大时，两种方法的计算误差都增大。变异系数不超过0.15时，PSFEM1在两种工况下与MCS的误差分别小于4.66%和4.09%，PSFEM2在两种工况下与MCS的误差分别小于6.28%和4.52%。对比之下，在不同变异系数下，在工况一情况下较多采用PSFEM1，在工况二情况下可以用PSFEM2代替PSFEM1。

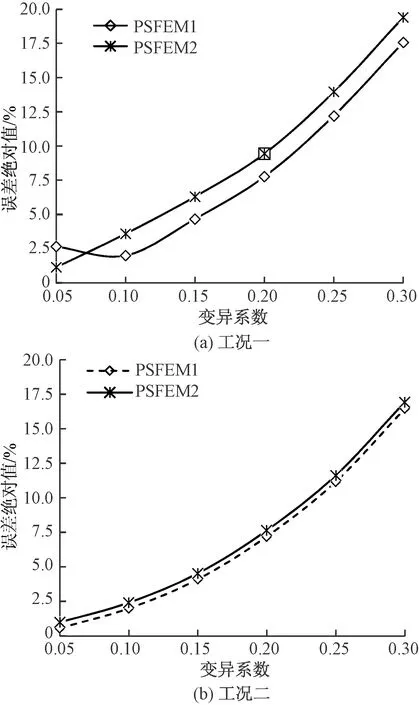
图3 不同工况下比较PSFEM1和PSFEM2的计算结果

将工况一情况下PSFEM1和MCS的计算结果进行比较，比较结果如图4所示。

从图4可以看出，随着变异系数的增大，两种方法计算的结构可靠指标都减小，从而说明随着随机参数变异系数的增大，箱梁的可靠度降低。当随机参数变异系数小于0.15时，PSFEM1和MCS的计算结果非常相近。当随机参数变异系数大于0.15时，两者的计算结果逐渐偏离，变异系数为0.20、0.25和0.30时的偏离误差分别为7.75%、12.20%和17.57%。以上说明只有随机参数小变异时，PSFEM1具有较好的计算精度。

图4 工况一下比较PSFEM1和MCS的计算结果

在工况一下，采用基于验算点的可靠度算法(记为PSFEM-1)；在工况二下，采用简化迭代算法(记为PSFEM-2)。计算箱梁中点的可靠指标及其与随机场变异系数的关系，并将计算结果进行对比，对比结果如图5所示。

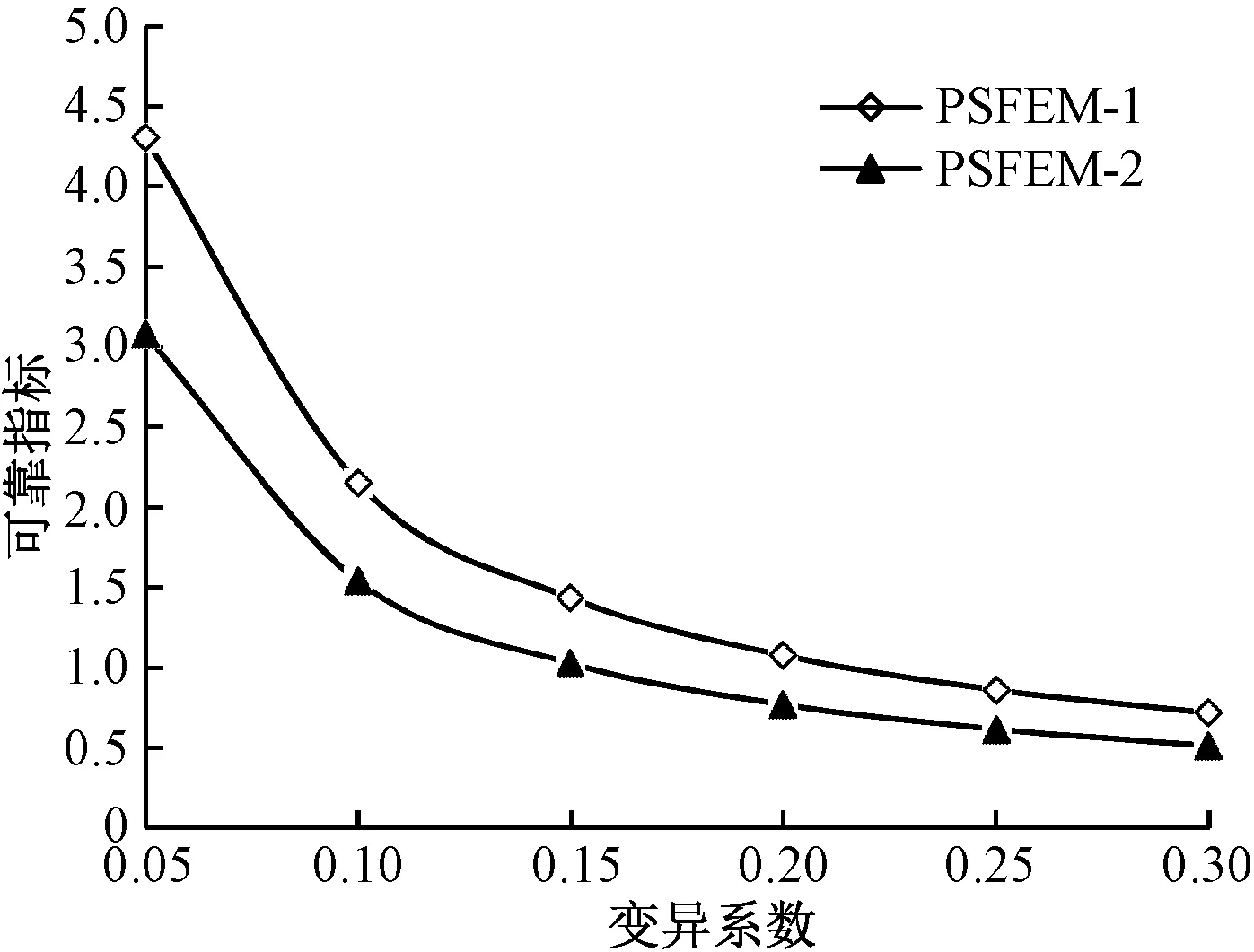
图5 比较PSFEM-1和PSFEM-2的计算结果

从图5可以看出，随着随机参数变异系数的增大，两种不同工况下计算的可靠指标都逐渐减小，说明随机参数的变异性对箱梁结构的可靠度是不可忽视的影响因素。在同一变异系数下，PSFEM-1的计算的结果大于PSFEM-2的计算结果，说明在弹性模量具有随机性的基础上，荷载具有随机性时，箱型梁的可靠度也会相应降低。

5 结论

基于箱梁附加挠度建立了箱梁可靠度分析的摄动随机有限元法，研究对比了基于验算点和简化迭代算法，得出如下结论。

(1)在弹性模量随机和弹性模量荷载随机两种工况下，基于验算点的迭代算法结果与其简化迭代算法的结果比较接近，误差分别小于1.83%和0.48%。

(2)在弹性模量随机情况下，在随机参数小于0.15时，基于验算点的迭代算法结果具有良好的计算精度，与基于蒙特卡洛有限元算法的结果误差不超过4.66%，其简化迭代算法计算结果误差是6.28%；在弹性模量荷载随机情况下，在随机参数小于0.15时，基于验算点的迭代算法及其简化迭代算法的结果都具有良好的计算精度，与基于蒙特卡洛有限元算法的结果误差不超过4.09%和4.52%。

(3)基本变量的随机性对箱型梁的可靠度有明显影响，参数变异性越大，可靠指标下降越大；在弹性模量具有随机性的基础上，荷载具有随机性时，箱型梁的可靠度也会相应降低。因此，分析和设计箱梁结构时，结构参数随机性的影响不容忽视。