刘财辉，凌 敏，钱 进

(1.赣南师范大学 数学与计算机科学学院，江西 赣州 341000；2.华东交通大学 软件学院，江西 南昌 330013)

0 引 言

粗糙集理论是由Pawlak[1]于1982年提出的一种主要用于处理不确定知识的工具.近年来,对粗糙集理论的研究取得了大量的研究成果[2-6].为使粗糙集更好地解决实际问题，Qian等人[7-8]在Pawlak粗糙集的基础上提出了乐观多粒度粗糙集和悲观多粒度粗糙集；Yang[9]在Qian的基础上进一步提出了一种基于优势关系的乐观多粒度粗糙集和悲观多粒度粗糙集.随着研究的深入，人们发现，知识与知识之间存在交叉的情况，因此覆盖粗糙集的概念应运而生.Zakowski[10]首先提出了覆盖广义粗糙集，将Pawlak粗糙集的全域划分推广为覆盖全域，并在此基础上建立了一对粗糙逼近运算；Tsang等[11]提出了一种基于最小描述的新型覆盖粗糙集模型；Zhu等[12]通过加强上、下近似之间的依赖，提出了一种新型的覆盖粗糙集模型.此外,一些其他学者也从不同角度对覆盖粗糙集做了大量的研究[13-17].

不确定性度量作为研究粗糙集的一个重要问题，Pawlak等人首先给出了粗糙精度、粗糙度的度量方法，然而事实表明这些方法不能准确度量现有信息粒度的划分.Beaubouef等人[18]用香农熵的概念来研究粗糙关系的不确定性度量；苗夺谦等[19-20]研究了粒计算与不确定性之间的关系；Yao[21]揭示了信息粒度与概念逼近的关系，用信息粒度来衡量不同粒度结构下的不确定性信息；李金海等[22]在多粒度形式背景下，将信息熵对信息的不确定性研究拓展至最优粒度选择，为多粒度形式背景下的不确定性研究提供了新角度；王国胤等[23]展开了信息论在粗糙集中的研究，将信息熵应用到粗糙集中的不确定性分析，并给出了条件熵下的数据约简新方法；Leung等[24]提出了在不完备信息系统下的最大一致块方法，可得到更精确的近似集；梁吉业等[25]研究了不同二元关系下信息系统信息粒的表示，建立了信息粒度与熵的互补关系，这统一了完备信息系统和不完备信息系统中的不确定性度量；Qian等[26-27]人定义组合熵与知识粒度的概念，以研究信息系统不确定性.随着粗糙集模型的扩展,许多学者对扩展模型中不确定性问题做了研究[28-31].

多粒度覆盖粗糙集模型作为多粒度粗糙集的推广，与实际应用更加贴近.为更清晰地对知识分类和推理，研究覆盖粗糙集模型中的不确定性问题是一件很有价值的工作.因此本文主要对多粒度覆盖粗糙集的不确定性进行了深入研究，具体内容如下:第1节给出了覆盖粗糙集和多粒度粗糙集的相关定义；第2节通过定义基于最小描述交的特征函数，定义了一类新的多粒度覆盖粗糙集模型，并讨论了不同类型的上下近似算子及性质；第3节从上、下近似和边界域两个角度定义了不确定性度量；第4节在4个UCI数据集上对三个模型进行了实验分析，并观察不确定性度量的变化情况，验证了本文所提方法的正确性和有效性；第5节进行了总结.

1 基本概念

1.1 覆盖粗糙集

定义1[32]设U是非空有限论域，C={C1,C2,…,Cn}是U的一个子集族，对于∪C=U，∀Ci≠∅，称C是U上的一个覆盖，〈U,C〉为一个覆盖近似空间.

定义2[32]设〈U,C〉为覆盖近似空间，对∀x∈U，x关于U的最小描述Md(x)定义为：

Md(x)={K∈C|x∈K∧(∀S∈C∧x∈S∧S⊆K⟹S=K)}.

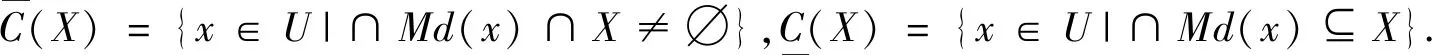
1.2 多粒度粗糙集

定义4[33]给定信息系统I=(U,AT,V,F),Ai⊆AT,i=1,2,…,m(m≤2|AT|)，对∀X⊆U,x关于X的支持特征函数定义如下：

2 基于支持特征函数的多粒度覆盖粗糙集

在覆盖粗糙集和多粒度粗糙集的基础上，为了描述多粒度覆盖粗糙集的基本特征及反映各个元素从属于覆盖集U的程度,我们给出了基于最小描述交的支持特征函数的概念，提出了一类基于支持特征函数下的多粒度覆盖粗糙集模型：广义多粒度覆盖粗糙集、乐观多粒度覆盖粗糙集和悲观多粒度粗糙集.为避免多粒度覆盖粗糙集在乐观条件下近似的定义过于宽松，知识粒度过于饱和；在悲观情况下近似的定义过于严格，知识粒度过于空缺，定义了一个参数β，以刻画最小描述交Md(x)与X的包含程度.

定义7设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，C={C1,C2,…,Cn}，对∀x∈U，支持特征函数定义如下：

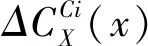
2.1 广义多粒度覆盖粗糙集(GMC)

定义8设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，C={C1,C2,…,Cn}，设定一个阈值β∈(0,1),对∀x∈U，广义多粒度覆盖粗糙集的上下近似定义为：

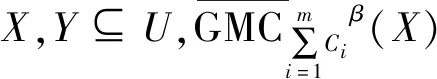
证明由于篇幅所限，证明略.

定理2设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，对∀X⊆U，当γ<β时满足:

证明由于篇幅所限，证明略.

2.2 乐观多粒度覆盖粗糙集(OMC)

定义9设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，C={C1,C2,…,Cn}，设定一个阈值β∈(0,1),对∀x∈U，乐观多粒度覆盖粗糙集的上下近似定义为：

2.3 悲观多粒度覆盖粗糙集(PMC)

定义10设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，C={C1,C2,…,Cn}，设定一个阈值β∈(0,1),对∀x∈U，悲观多粒度覆盖粗糙集的上下近似定义为：

以上两个模型的性质类似于定理1.

定理3设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，C={C1,C2,…,Cn}，设定一个阈值β∈(0,1)，对∀x∈U,有下列公式成立：

定理3可由定义8、定义9和定理2证明.

3 多粒度覆盖粗糙集的不确定性度量

本节在基于支持特征函数的多粒度覆盖粗糙集模型的基础上，提出了几种不确定性度量方法.从上下近似和边界域的角度出发，分别定义了两种类型的近似精度、粗糙度和近似质量，并研究了相关性质.

定义11设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，对∀X⊆U，X关于覆盖集C的第一类广义多粒度覆盖粗糙集的近似精度和粗糙度可以定义为：

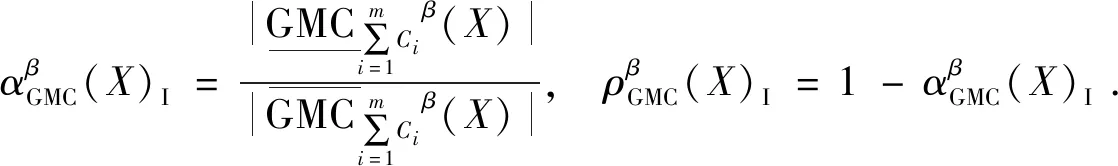
同理，X关于覆盖集C的第一类乐观多粒度覆盖粗糙集及悲观多粒度覆盖粗糙集的近似精度和粗糙度分别定义为：

定义12设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，对∀X⊆U，X关于覆盖集C在三种模型下的第二类近似精度和粗糙度可以定义为：

定义13设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，对∀X⊆U，X关于覆盖集C在三种模型下的近似质量可以定义为：

定理4设〈U,C〉为覆盖近似空间，C为U上的一个覆盖，对∀X⊆U，不确定性度量还存在如下关系：

此定理可由定义2.2～2.4和定理2.2证明.

4 实验分析

为进一步研究和验证广义多粒度覆盖粗糙集(GMC)、乐观多粒度覆盖粗糙集(OMC)及悲观多粒度覆盖粗糙集(PMC)模型下三种不确定性度量的关系，我们从UCI数据库中获取了Iris、German、Stalog、AnuranCalls(MFCCS)4个数据集进行实验比较分析，数据集分别用U1,U2,U3,U4表示,具体信息如后面的表1所示.该实验是在实验环境为64位、Intel(R)Core(TM)i7-8700CPU@3.20GHz的台式电脑下完成的，实验软件为MATLAB2019a，部分实验算法如下：

Algorithm1:Uncertaintymeasurementofgeneralizedmulti-granularitycoveringroughsetsINPUT:d,β,U={U1,U2,…,Un},C={C1,C2,…,Cn}OUTPUT:αβGMC(X)I,ρβGMC(X)I,αβGMC(X)II,ρβGMC(X)II,ωβGMC(X)1. fori=1:ndo2. forj=1:mdoP(i,:)=(P(i,:)-min(P(i,:)))/(max(P(i,:))-min(P(i,:)));3. end4. end5. fori=1:ndo//%CalculatetheEuclideandistancebetweeneachobject6. forj=1:mdoDis(x,y)=sqrt(∑(xi122xi1∗xi2+xi22))7. end8. end9. fori=1:mdo//%Calculatethetolerancerelationshipofeachobject10. forj=1:mdo11. ifDis(x,y)≤dthenCi(xi)=Ci(xi)∪{xj}.12. end13. end14. end15. fori=1:mdoΔCCiX(x)=0,ΔCCi～X(x)=016. forj=1:mdo17. if∩Md(x)⊆XthenΔCCiX(x)=ΔCCiX(x)+118. elseΔCCiX(x)=ΔCCiX(x)19. end20. if∩Md(x)⊆～XthenΔCCi～X(x)=ΔCCi～X(x)+121. elseΔCCi～X(x)=ΔCCi～X(x)22. end23. end24. endGMC∑mi=1Ciβ(X)=GMC∑mi=1Ciβ(X)∪xi25. fori=1:ndo26. ifΔCCiX(x)m≥βthenGMC∑mi=1Ciβ(X)=GMC∑mi=1Ciβ(X)∪xi27. end28. if1-ΔCCiX(x)m≥1-βthenGMC∑mi=1Ciβ(X)=GMC∑mi=1Ciβ(X)∪xi29. end30. endreturnαβ(X)I,ρβGMC(X)I,αβGMC(X)II,ρβGMC(X)II,ωβGMC(X)

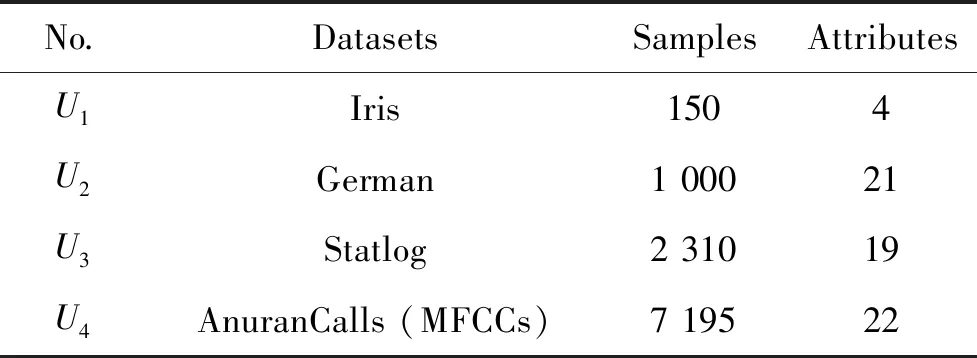
表1 数据集信息Tab.1 Datasets information

对算法1的时间复杂度进行分析：步骤1至8，对数据进行归一化处理，并计算对象之间的欧式距离，时间复杂度为O(|U|2×|Ci|×n) (n为论域的个数)；步骤9至14、步骤15至23，分别计算覆盖对象之间的关系、最小描述交对给定概念及其补集的支持特征函数值，时间复杂度均为O(|U|2×m)；步骤24至30，计算覆盖空间下的上、下近似值，时间复杂度为O(|U|).

主要实验步骤如下：

1) 将U1,U2,U3,U4,数据集按90%等比例随机取样,并归一化处理,使所取样本取值置于[0,1]区间.

2) 计算每个数据集所取样本归一化后欧氏距离,并设定相应的距离阈值为:d1=0.5,d2=0.5,d3=0.4,d4=0.08,通过调参设定信息水平参数阈值β=0.3.

3) 计算三种多粒度覆盖粗糙集在阈值条件下对应的上下近似及支持特征函数值，由此得到广义多粒度覆盖粗糙集(GMC)、乐观多粒度覆盖粗糙集(OMC)及悲观多粒度覆盖粗糙集(PMC)在U1,U2,U3,U4下的近似质量ω、两种类型的近似精度αI,II和粗糙度βI,II.

4) 实验进行5次随机采样，重复上述3个步骤，得到5次实验结果，如图1～图3所示.

图1 两种类型的近似精度Fig.1 Two types of approximation accuracy

图2 两种类型的粗糙度Fig.2 Two types of roughness

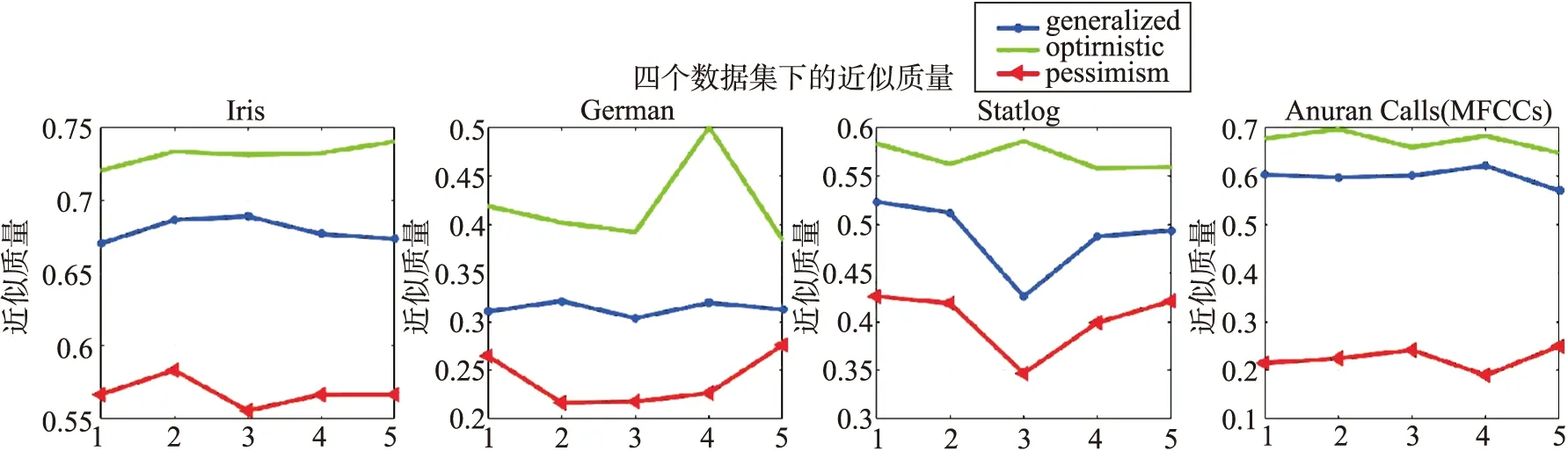
图3 近似质量Fig.3 Approximate quality

为更直观、简洁地看到三个模型在不同度量方法下的差异，可从实验结果图1～图3得出以下结论：

图1展示了广义,乐观和悲观三种多粒度覆盖粗糙集在四个数据集下两种类型近似精度的关系，发现两种类型在乐观条件下的近似精度均大于广义条件下的近似精度且大于悲观条件下的近似精度;图2展示了三种模型在四个数据集下的两种类型粗糙度的关系,发现两种类型在悲观条件下的粗糙度均大于广义条件下的粗糙度且大于乐观条件下的粗糙度；图3展示了三种模型在四个数据集下近似质量的关系,发现乐观条件下的近似质量大于广义条件下的近似质量且大于悲观条件下的近似质量.可见该实验结果满足定理4.

在对象选择时，乐观多粒度覆盖粗糙集过于宽松，无法准确地描述概念.主要原因是乐观多粒度覆盖粗糙集在选择对象时具有积极的描述，对象只需在至少一个域下支持该概念即可.容易造成在下近似中可能会增加许多无用的描述：在上近似中容易丢失有用的描述，这将使概念的描述不准确.相反，悲观多粒度覆盖粗糙集对域的概念要求则过于严格.

介于悲观、乐观多粒度覆盖粗糙集模型在实际应用中均存在局限性，本文提出了一种新的多粒度粗糙集模型，它通过调节信息参数β∈(0,1)来控制对象的选择，阈值用于控制对象在大多数域中被正面描述，低于该阈值的对象则被删除.

从图1～图3，我们可以看到不同模型在不同数据集的结果是不一致的，不同度量方法得到的度量结果也并不完全一致.因此在实际应用中，不同领域应根据自己的需求选择模型，还应根据不同的方案选择合理的度量方法.

5 结 论

本文从多粒度的角度，结合覆盖粗糙集形成多粒度覆盖粗糙集.在支持特征函数的背景下加入信息参数，先后提出了三种多粒度覆盖粗糙集的扩展模型：广义多粒度覆盖粗糙集、乐观多粒度覆盖粗糙集和悲观多粒度覆盖粗糙集，并讨论了它们的相关定理和性质.为更深入研究多粒度覆盖粗糙集，我们讨论了在不同情况适用于三种模型的不确定性度量方法.最后我们设计了一个计算不确定性度量的算法，并用四个数据集对该算法进行了验证.实验表明，广义多粒度覆盖粗糙集模型具有更广泛的适用性.