面向连续离散系统的自适应最大相关熵滤波算法

2022-06-10胡浩然陈树新吴昊何仁珂吴强张喜庆

西安交通大学学报 2022年6期

胡浩然,陈树新,吴昊,2,何仁珂,吴强,张喜庆

(1.空军工程大学信息与导航学院,710077,西安;2.地理信息工程国家重点实验室,710054,西安;3.复杂航空系统仿真重点实验室,100076,北京;4.解放军95894部队,100076,北京;5.华恒智禾电子信息技术有限公司,710077,西安)

在目标跟踪[1-2]领域,离散-离散时间系统将目标运动模型及其测量模型均视为离散模型。但是,考虑目标运动的实际情况,运动模型在本质上应是连续的,而其有间隔的测量是离散的,这样的系统称为连续-离散时间系统[3]。相比较于传统跟踪算法常采用的离散-离散系统模型,连续-离散系统的数学解算方式精度更高,在目标跟踪领域更具优势[4]。

文献[4]将连续-离散时间系统与容积准则相结合,形成了连续-离散容积卡尔曼滤波(continuous-discrete cubature Kalman filter,CD-CKF)算法。该算法以随机微分方程(stochastic differential equation,SDE)描述连续时间目标运动模型,而SDE的求解精度又很大程度上影响着滤波的性能。文献[5]提出了基于1.5阶的It-Taylor算法,有效解决了连续时间的预测问题,但同时存在精度上限不高的缺点。为进一步提高状态估计的精度,文献[6]将基于SDE的连续模型描述为状态期望和协方差的形式,进而用高阶数值近似算法对连续模型进行了求解。文献[7]采用了一种嵌套式的隐式高阶龙格-库塔算法,解决了连续-离散扩展卡尔曼滤波(continuous-discrete extended Kalman filter,CD-EKF)的状态估计问题,该算法也成功应用于CD-CKF算法,有效提高了滤波的精度[8]。文献[9]采用自适应步长对上述数值近似算法完成了优化,进一步提高了连续-离散滤波算法的性能和效率。

以上提高滤波精度的算法都是在假设测量噪声为高斯型的理想条件下建立的。但是,在实际测量环境中,信号干扰等恶劣条件会导致非高斯噪声或异常误差的出现。如果不加以处理,滤波就会不准确甚至发散。对于此类测量不确定问题,有关学者在离散-离散时间系统做了充分的研究,提出了多种鲁棒滤波算法。文献[10]采用Huber代价函数来降低异常数据的权重;Wu等[11]提出了基于广义M估计的鲁棒CKF算法,无需考虑降权函数的经验阈值和异常误差的统计特征信息。近年来,相关熵准则[12]因能够有效抑制非高斯噪声而受到广泛关注。作为一种局部相似性度量,其与仅使用测量量二阶矩信息的经典最小均方误差准则相比,能够充分利用测量量的更高阶信息。因此,相关熵理论适用于受非高斯噪声污染的随机系统。最大相关熵准则(maximum correntropy criterion,MCC)已成功应用于离散-离散时间系统滤波中[13-14],提高了算法的鲁棒性。

为了进一步提升目标跟踪精度和鲁棒性,本文将改进的MCC代价函数(传统的MCC滤波算法存在数值问题)扩展到连续-离散时间系统,同时引入自适应因子和平方根滤波技术,提出了一种具有鲁棒机制的连续-离散目标跟踪算法。该算法使用连续-离散模型描述目标运动,利用所提MCC算法处理测量噪声,由不同测量环境确定自适应因子的取值,并通过自适应因子对观测噪声的协方差矩阵在线调整,进而完成对状态的估计以及协方差的实时更新。同时,为保证误差协方差矩阵的正定性和对称性,将其与平方根滤波技术相结合,从而得到了鲁棒平方根连续-离散自适应最大相关熵容积卡尔曼滤波(robust square-root continuous-discrete adaptive maximum correntropy cubature Kalman filter,RSRCD-AMCCKF)算法。仿真验证结果表明,本文算法能够有效处理测量中可能出现的高斯、非高斯噪声以及测量突发异常的情况。

1 连续-离散系统目标跟踪模型和平方根连续-离散容积卡尔曼滤波算法

1.1 连续离散系统目标跟踪模型

在连续-离散目标跟踪系统中,目标运动模型为连续时间模型,测量模型是离散时间模型。考虑到随机扰动,连续时间目标运动模型可以描述为随机微分方程的形式

(1)

式中:x(t)是n维的状态向量;f为状态转移函数;w(t)是n维标准布朗运动;Q为布朗运动的协方差矩阵。

依据状态期望和协方差进行状态估计有利于提高连续-离散滤波算法的精度,期望和协方差可表示为

(2)

(3)

离散时间测量模型为

zk=h(xk,k)+vk

(4)

式中:zk是实际观测值;h为观测函数;vk是观测噪声,指代高斯或非高斯噪声;k是指离散的时间测量点。

1.2 平方根连续离散容积卡尔曼滤波算法

1.2.1 时间更新

在平方根连续-离散容积卡尔曼滤波(square-root continuous-discrete cubature Kalman filter,SRCD-CKF)算法中,状态容积点可定义为

(5)

式中:ξi是容积点集;S(t)为协方差矩阵P(t)的下三角矩阵,满足P(t)=S(t)ST(t)。

基于容积准则,期望和协方差可重新表示为

(6)

(7)

式中ε和W是容积参数,定义为

(8)

其中,I2n表示维数为2n的单位矩阵,1是单位列向量,⊗代表Kronecker积。

对协方差传播的计算,本文采用文献[15]提出的平方根协方差计算算法,将其与容积准则结合,并用高阶数值近似算法进行求解

(9)

(10)

式中:Bi,j是Φ(B)的第i行、第j列的元素;Φ(B)作为判断矩阵,完成平方根形式的误差协方差矩阵更新。B(t)的定义为

B(t)=S-1(t)[X(t)WFT(X(t))+

F(X(t))XT(t)+Q(t)]S-T(t)

(11)

(2)协方差分解,计算式为

P(tk)=S(tk)ST(tk)

(12)

(3)计算状态容积点,公式为

(13)

(4)状态容积点传播,计算式为

(14)

(5)计算状态预测值,公式为

(15)

(6)求解预测平方根协方差,计算式为

(16)

1.2.2 测量更新

测量更新流程如下。

(1)计算状态容积点,公式为

Sk|k-1=S(tk)

(17)

(18)

(2)容积点的测量传播,计算式为

Zi,k|k-1=h(Xi,k|k-1,k)

(19)

(3)计算测量预测值,公式为

(20)

(4)构建测量加权中心矩阵,计算式为

(21)

(5)计算新息协方差矩阵,公式为

(22)

(6)构建状态加权中心矩阵,计算式为

(23)

(7)计算交叉协方差矩阵,公式为

(24)

(8)计算连续-离散的容积增益,公式为

(25)

(9)计算状态估计值,公式为

(26)

(10)更新协方差矩阵,计算式为

(27)

2 基于连续-离散系统的自适应最大相关熵平方根容积卡尔曼滤波算法

2.1 最大相关熵准则

相关熵是用于衡量两个随机变量之间相似性的一种新方法。对于给定的两个随机变量X和Y,相关熵定义为[12]

V(X,Y)=E[κ(X,Y)]=∬κ(x,y)dFX,Y(x,y)

(28)

式中:E[·]为数学期望;FX,Y(x,y)为联合概率密度函数;κ(·)为梅瑟型正定核函数。核函数的选择决定了相关熵的求解方式,本文选取高斯核作为相关熵的核函数,其定义为

(29)

式中e=x-y,σ>0是核函数的核带宽。

实际中,联合概率密度函数通常是难以获取的,且所获得的样本数据采样点也是有限的。因此,相关熵可以通过T个样本数据采样点进行估计

(30)

(31)

由式(31)可以看出,随机相关熵信息包含了变量误差X-Y的所有偶数阶矩。因此,只要选择合适的核带宽,就可以获取更高阶的信息。对受高斯噪声污染的系统,与使用测量值二阶矩信息的最小均方误差准则相比,相关熵是完全可以用来描述其统计信息的。对于测量中出现的非高斯噪声,最大相关熵准则能够利用测量量的更高阶信息,对处理非高斯随机系统也是十分有效的。

2.2 鲁棒平方根连续离散自适应最大相关熵容积卡尔曼滤波算法

在连续时间状态模型中,其过程噪声是高斯形式的,但离散的测量噪声是非合作的。因此,本文将加权最小二乘(weighted least squares,WLS)代价函数与最大相关熵准则相结合,定义新的相关熵代价函数

(32)

(33)

(34)

考虑式(32)所示的代价函数,滤波算法的最终目的是获得xk的最优估计,即

(35)

式(35)的最优解可通过求解极值获得

(36)

式中自适应因子Lk的表达式为

(37)

这里由最大相关熵准则得到的自适应因子Lk是一个标量,可通过式(29)完成计算,它很容易分离并且避免了零矩阵求逆的数值计算问题。

为了保证当σ→∞时,此算法能够收敛于传统的CD-CKF算法,令γ=1、β=-2σ2,则式(36)可重新表述为

(38)

两边移项,提取公共项可以得到

(39)

由此获得的方程式(39)是一个不动点方程,因为Lk与xk相关,可以通过固定点迭代算法求解。经一次迭代后即可得到所需的状态更新值与滤波增益

(40)

(41)

相关的误差协方差矩阵的更新计算式为

(42)

(43)

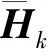
(1)当测量值发生较大突变或受噪声影响较大,即‖zk‖∞→∞时,传统的相关熵滤波算法[16]会出现零矩阵的求逆计算,这会导致原有的滤波算法失效,而本文提出的RSRCD-AMCCKF算法则可以避免上述数值计算问题。

(2)高斯核带宽σ在很大程度上影响滤波算法的精度。已有研究表明,σ较小时对非高斯测量噪声具有更强的鲁棒性[16]。但是,当σ过小时,算法的滤波性能会退化较为严重,甚至会出现滤波发散的情况。针对连续-离散时间系统的实际情况,根据σ的取值对自适应因子进行调整,以便更加合理地处理不同测量情况也是十分重要的。

3 仿真与分析

仿真中考虑典型的空中交通管制场景,跟踪目标在水平面内以一定的转弯率做协调转弯运动[17-18],分析本文提出的目标跟踪算法在测量噪声为高斯噪声、测量噪声为非高斯噪声、测量值发生突变这3种场景下的性能变化。目标的协调转弯运动是一种典型的非线性运动,其连续时间运动模型可以用随机微分方程表示。

采用CKF算法[18]、MCCKF算法、SRCD-CKF算法、基于Huber两段权函数的连续-离散鲁棒(Huber robust square-root continuous-discrete cubature Kalman filter,HRSRCD-CKF)算法、基于P-Huber三段权函数的连续-离散鲁棒(M-estimation based robust square-root continuous-discrete cubature Kalman filter,MRSRCD-CKF)算法作为对比算法。HRSRCD-CKF算法和MRSRCD-CKF算法可以理解为Huber鲁棒函数在本文提出的连续-离散系统框架中的应用,其较离散-离散系统的滤波精度更高[19]。MCCKF算法采用本文提出的最大相关熵算法,σ取值参考文献[20],HRSRCD-CKF算法中异常误差的判别门限值取为1.345,而MRSRCD-CKF算法中的α分位点取为α1=0.1,α2=0.1%。

离散时间的非线性测量模型为

zk=arctan(y(tk)/x(tk))+vk

(44)

式中vk为测量噪声,具体表达形式视仿真场景进行定义。

克拉美罗下界是目标参数跟踪误差的下界,它提供了滤波算法理论达到的最好均方误差。克拉美罗下界在k时刻的定义为

(45)

文献[21]已证明,Fisher信息矩阵Mk的递归计算式为

(46)

考虑到本文采用纯方位跟踪系统,Mk在该系统中的表达式[21]为

(47)

式中

(48)

ψk是观测函数的雅可比矩阵,其具体定义为

(49)

为了评估各算法的性能,分别定义位置量、速度量的均方根误差(root mean square error,RMSE),计算式为

(50)

(51)

(1)仿真场景1,测量噪声为高斯噪声。高斯条件下的滤波问题是目标跟踪算法的基础,目标跟踪过程常常讨论该条件下滤波算法的精度问题[22-23]。测量噪声vk满足0均值的高斯分布,即vk～N(0,Rk),本次仿真中Rk的初始值为一维常值0.001。当高斯核带宽σ取不同值时,所提RSRCD-AMCCKF算法的eRMS,x和eRMS,v如表1所示。

由表1可知:当高斯核带宽σ不同时,RSRCD-AMCCKF算法表现出了不同的性能,σ过小或过大都会降低滤波的精度;当σ=0.1时,滤波发散;当σ越来越大时,RSRCD-AMCCKF滤波性能逐渐趋近于SRCD-CKF算法,符合之前的理论推导;当σ=50时,RSRCD-AMCCKF滤波精度仍高于SRCD-CKF算法。

表1 高斯条件下不同核带宽时的算法精度

高斯核带宽σ=5时,各算法的eRMS,x和eRMS,v分别如图1、图2所示。

图1 高斯噪声下各算法的位置均方根误差比较Fig.1 Comparison of position root mean square error of each algorithm under Gaussian noise

图2 高斯噪声下各算法的速度均方根误差比较Fig.2 Comparison of velocity root mean square error of each algorithm under Gaussian noise

由图1和图2可知:当测量噪声为高斯噪声时,各算法前期走势大致相同,都能够随着测量次数的增加趋于收敛,其中,连续-离散滤波算法较离散-离散滤波算法表现出了更高的精度;MCCKF算法较CKF算法略有优势,其精度比较接近连续-离散算法,HRSRCD-CKF和MRSRCD-CKF较原始的SRCD-CKF算法有小幅波动,在测量正常的情况下精度基本持平;RSRCD-AMCCKF相比较于以上算法最接近于CRLB,滤波性能更优,这是因为最大相关熵准则能够利用测量量的更高阶信息,将高斯核应用于估计误差矩阵的每个元素,与SRCD-CKF的结合效果更好。

(2)仿真场景2,测量噪声为非高斯噪声。在目标跟踪过程中,由于复杂目标不同部位的散射强度和相对相位的随机变化,造成回波相位波前面的畸变,波前在接收天线口径面上的倾斜和随机摆动必然引起测量误差,这种现象引起的测量噪声称之为闪烁噪声。闪烁噪声分布与高斯分布的主要差别在于尾部较长,而在中心区域则类似于高斯形状,常表现出非高斯特征。目前,针对被污染目标的这一特性,常采用具有不同方差的高斯噪声加权对闪烁噪声建模,以此来表示测量中出现的非高斯误差[24],即测量噪声vk为高斯混合噪声,vk～0.99N(0,Rk)+0.01N(0,500Rk)。当σ不同时,RSRCD-AMCCKF算法在非高斯条件下的eRMS,x和eRMS,v如表2所示。

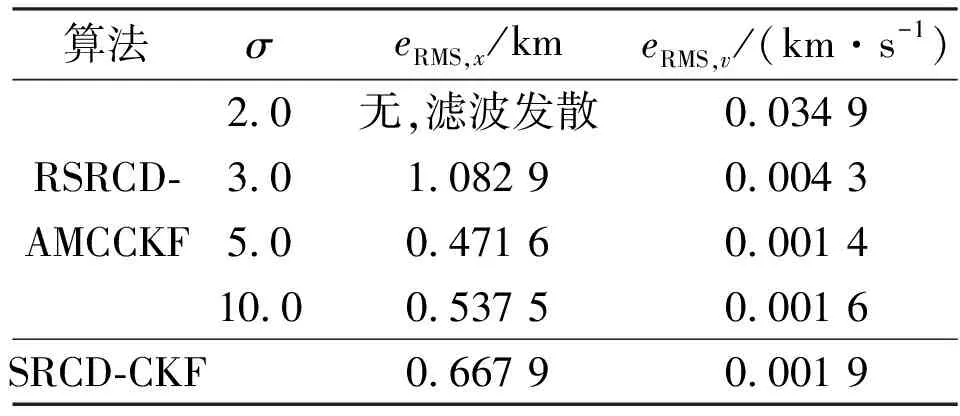
表2 非高斯条件下不同核带宽时的算法精度

由表2可知:能够对非高斯噪声起到抑制作用的σ发生了变化,相比于高斯条件下RSRCD-AMCCKF算法的滤波精度有所降低,但合适的σ仍能对测量中出现的非高斯噪声起到一定的抑制作用。因此,根据不同测量环境选择是比较重要的。

在非高斯条件下,σ=5时各算法的eRMS,x和eRMS,v分别如图3和图4所示。

图3 非高斯噪声下各算法的位置均方根误差比较Fig.3 Comparison of position root mean square error of each algorithm under non-Gaussian noise

图4 非高斯噪声下各算法的速度均方根误差比较Fig.4 Comparison of velocity root mean square error of each algorithm under non-Gaussian noise

由图3和图4可知:当测量噪声为非高斯噪声时,各算法的误差均出现了不同程度的增大,但在滤波精度上连续-离散算法仍表现出了相对较高的精度;HRSRCD-CKF算法和MRSRCD-CKF算法不能够对非高斯测量噪声起到抑制作用,算法基本失效;MCCKF算法具备一定程度的抑制效果,但稳定性不高,这可能与核带宽的取值有关;RSRCD-AMCCKF算法能够对非高斯噪声起到较好的抑制作用,最终表现出相对较高的收敛精度,体现了MCC算法在处理非高斯噪声问题上所具有的优势。

图5 测量异常时各算法的位置均方根误差比较Fig.5 Comparison of position root mean square error of each algorithm under abnormal measurement

图6 测量异常时各算法的速度均方根误差比较Fig.6 Comparison of velocity root mean square error of each algorithm under abnormal measurement

由图5和图6可知:当测量发生异常时,不具备鲁棒性的CKF算法和SRCD-CKF算法误差陡然增加,CKF算法较SRCD-CKF算法精度稍低,而其他算法均有效抵制了异常测量。RSRCD-AMCCKF算法在受到干扰时表现出了更好的鲁棒性,对异常测量抑制的效果最为明显。HRSRCD-CKF算法、MRSRCD-CKF算法和MCCKF算法抑制效果稍差。同时,以连续-离散算法跟踪目标运动的RSRCD-AMCCKF算法较MCCKF算法拥有更高的精度,其收敛精度更趋向于CRLB曲线,说明本文提出的RSRCD-AMCCKF算法能够较好地实现滤波精度和鲁棒性的统一。