樊露露，套格图桑

（内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022）

0 引言

非线性发展方程（NLEEs）描述了流体力学、等离子体、光学、声学、传热学、经典力学等物理分支中复杂非线性现象的演化过程。浅水波方程是非线性方程中的一类重要方程，文献［1］给出了（1+1）维广义浅水波方程的变量分离解，文献［2］给出了扩展（2+1）维浅水波方程的精确相互作用解。近年来，对于广义（3+1）维浅水波方程的研究成果较多。这里包括对广义（3+1）维浅水波方程的一类精确解［3-4］，新周期孤立波解［5］，块解［6］，相互作用解［7］，以及弹性孤子和湮没孤子［8］，等。

目前为止，一个非线性系统是否可积还没有一个完全确定和统一的定义，所研究的可积性是指不同意义下的可积性，所以在说一个非线性系统是可积的时候通常会指明它是在何种意义下的可积。例如：Painlevé 可积［9］、Lax 可积、Liouvile 可积、反散射可积［10］和对称可积等。

自韦斯（J.Weiss）、泰伯（M.Tabor）、卡列（G.Carnevale）提出对偏微分方程的Painlevé 方法以来，该方法在讨论偏微分方程的可积性及求解方程的精确解上已有了很大的进展。以此研究了许多可积的偏微分方程，如（3+1）维Burgers 方程［11］、（3+1）维广义KP 方程［12］等。

除了对于系统可积性的研究，在此基础上还可以得到许多其他的重要结果，如Bäcklund 变换、精确解等，如对Burgers 方程［13］的研究。

因此，本文首先利用Painlevé 分析法研究广义（3+1）维浅水波方程的可积性；再根据截断的Painlevé展开式研究广义（3+1）维浅水波方程的Bäcklund 变换；由Bäcklund 变换，得到广义（3+1）维浅水波方程的精确解；最后利用Hirota 双线性方法，获得广义（3+1）维浅水波方程新的复合解。

1 广义（3+1）维浅水波方程的Painlevé 可积与Bäcklund 变换

1.1 广义（3+1）维浅水波方程的Painlevé 可积

对于广义（3+1）维浅水波方程

假设方程的解可写成

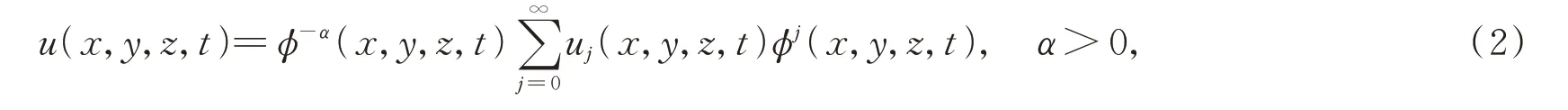
这里uj(x，y，z，t)(j=0，1，2，…)是t的解析函数，u0≠0。

欲验证该方程的Painlevé 性质，主要分为以下三个步骤：领头项分析、确定共振点和验证共振条件。

（1）领头项分析：由领头项分析得

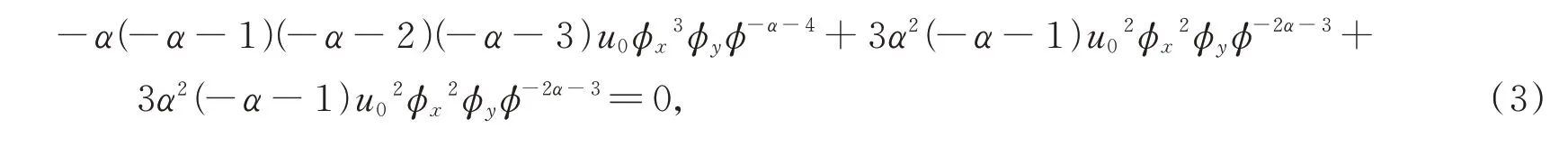
由（3）式得

（2）确定共振点：将（4）式代入（2）式，得

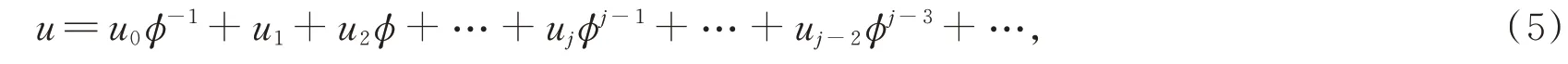
将（5）式及其各阶偏导数代入（1）式，比较φ的各次幂的系数，有

将u0=2φx代入（6）式，自动满足

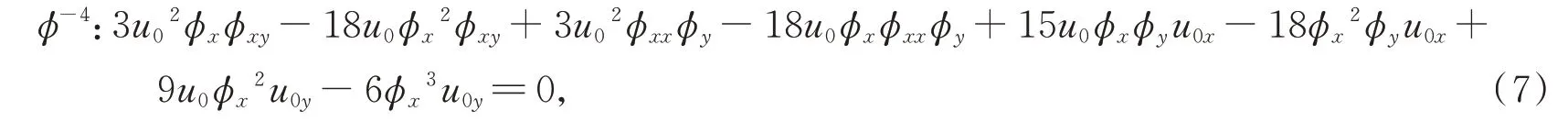
将u0=2φx代入（7）式，化简整理得方程（7）为恒等式。

同理可得φ-3，φ-2，φ-1的系数关系式，化简整理得

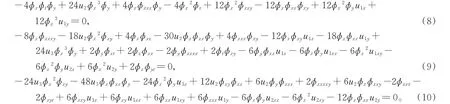
由φj-5的系数关系式可得uj的递推关系式为

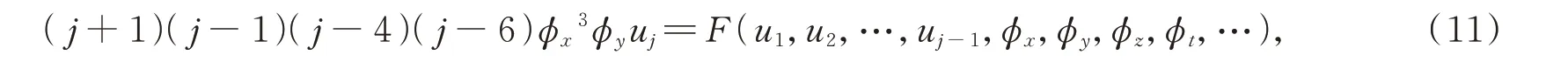
右端只与低于uj的u1，u2，…，uj-1及φx，φy，φz，… 有关，由（11）式可知，共振点为j=1，4，6。

（3）验证共振条件：为了计算的简便性，此处采用Krustal 简化方法，设

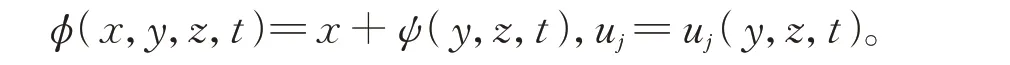
根据φ的各次幂关系式得到u1任意，u4任意，

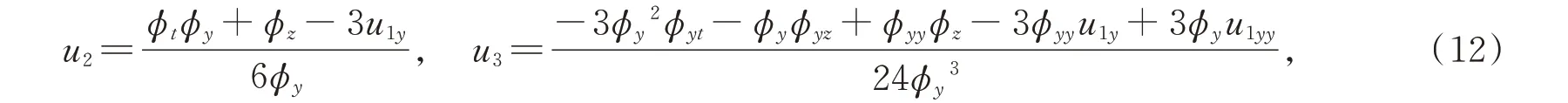
由于u5的表达式太长，这里不做过多的陈列。当j=6 时，根据φ的系数关系式，可得一个关于φ(x，y，z，t)和u1(y，z，t)的方程

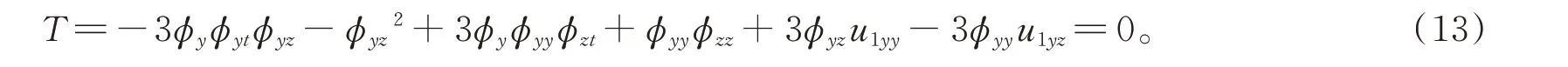
当φ(x，y，z，t)和u1(y，z，t)满足

方程（13）成立，在j=6 处的兼容性条件满足。即广义（3+1）维浅水波方程在约束条件（14）下是Painlevé可积的。

1.2 广义（3+1）维浅水波方程的Bäcklund 变换

在非线性系统中，Bäcklund 变换的研究是一重要研究课题，它在孤子理论的发展中有着非常重要的贡献。利用Painlevé 分析可以很方便地得到非线性系统的Bäcklund 变换。

定理根据以上讨论可知方程（1）是条件可积的，通过其截断展开式

得到线性方程

它将非线性的广义（3+1）维浅水波方程变成（16）的线性方程，截断Painlevé 展开给出了下述方程（1）和方程（16）的Bäcklund 变换。

推论若φ是方程（16）的一个解，则由方程（15）给定的也是方程（1）的解。

2 广义（3+1）维浅水波方程的精确解与复合解

2.1 广义（3+1）维浅水波方程的精确解

通过一系列变量分离法可求得方程（16）的解为

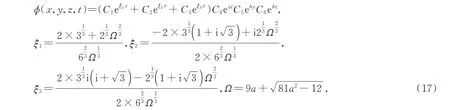
其中，C1，C2，C3，C4，C5，C6，a，b为任意常数。由推论得方程（1）的解为

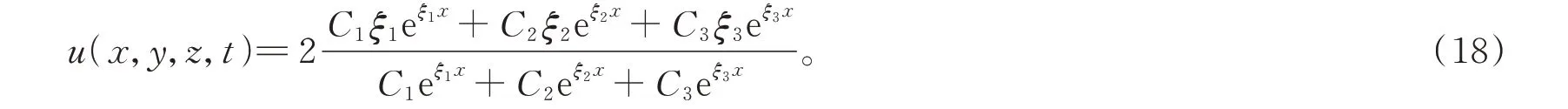
2.2 广义（3+1）维浅水波方程的复合解

对于（1）式，先使用变换

其中f=f(x，y，z，t)，得到方程的双线性形式

式中D算子为Hirota 双线性算符。

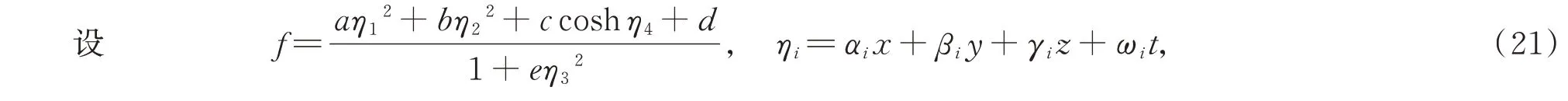
式中αi，βi，γi，ωi(i=1，2，3，4)，a，b，c，d，e为待定常系数。

取a=b=1，c=e=0，得到文献［4］中（9）式的形式解，取a=b=1，e=0，得到文献［4］中（17）式的形式解。

将（21）式代入（20）式，并令η1，η2，η3，sinhη4，coshη4的各次幂系数等于零，利用符号计算系统Mathematica得到以下结果。

情形1

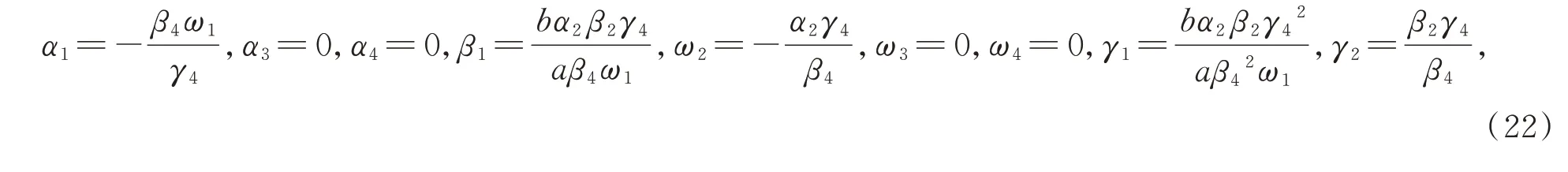
α2，β2，β3，β4，γ3，γ4，ω1，a，b，c，d，e为任意常数，（22）式需满足a≠0，β4≠0，γ4≠0，ω1≠0，得到方程（1）如下解，

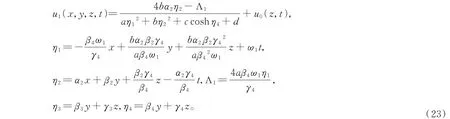
取a=2，b=-2，c=-2，d=-3，e=4，α2=4，β2=-1，β3=1，β4=-2，γ3=4，γ4=2，ω1=2，u0(z，t)=cn(5z-t，k)，。其特征如图1 所示。

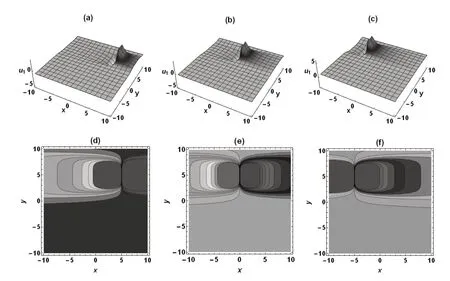
图1 （23）式关于x，y 的三维图及对应的等高线图Fig.1 The 3D plots and contour plots related to x and y corresponding to formula（23）

情形2

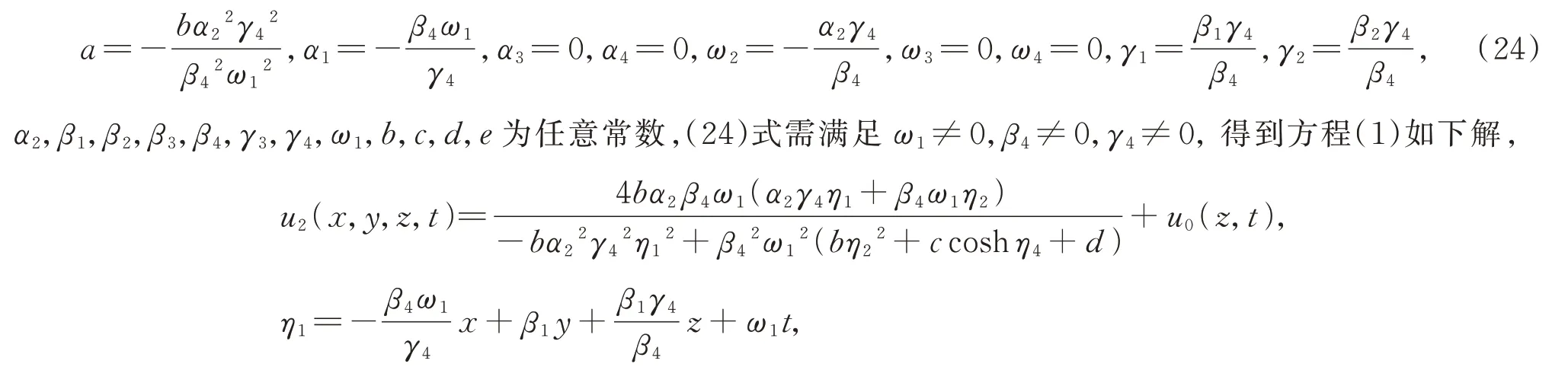
情形3

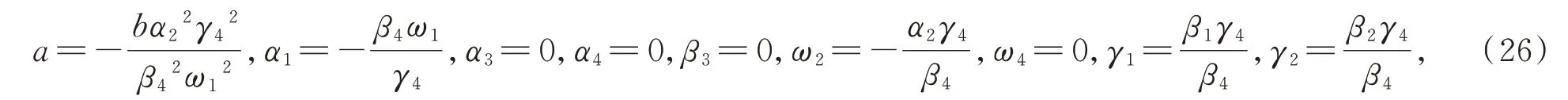
α2，β1，β2，β4，γ3，γ4，ω1，ω3，b，c，d，e为任意常数，（26）式需满足ω1≠0，β4≠0，γ4≠0，得到方程（1）如下解，

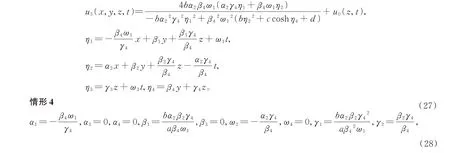
α2，β2，β4，γ3，γ4，ω1，ω3，a，b，c，d，e为任意常数，（28）式需满足a≠0，β4≠0，γ4≠0，ω1≠0，得到方程（1）如下解，

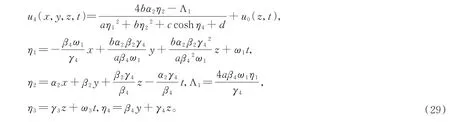
3 结论

本文利用Painlevé 分析法证明了广义（3+1）维浅水波方程在Painlevé 意义下是可积的；根据截断的Painlevé 展开式得到了广义（3+1）维浅水波方程与线性方程之间的Bäcklund 变换；通过得到的Bäcklund 变换，构造了广义（3+1）维浅水波方程新的精确解；利用Hirota 双线性方法，求得广义（3+1）维浅水波方程新的复合解。更加说明了广义（3+1）维浅水波方程的解的丰富性。

通过对系数取不同的值，得到文献［4］中部分解的形式。文献［11］和文献［12］研究了（3+1）维广义KP 方程和（3+1）维Burgers 方程的Painlevé 性质，文献［6］利用Hirota 双线性方法，得到了广义（3+1）维浅水波系统的块解及相互作用解，本文在其基础上得到了方程（1）的可积性、方程（1）与线性方程之间的Bäcklund 变换，通过分离变量及Hirota 双线性方法得到了方程（1）的精确解以及复合解，文献［11］和文献［12］均未研究其与线性方程之间的Bäcklund 变换。