安徽省合肥一六八中学 武前炜 （邮编：230601）

数学家奥加聂相曾经说过：“必须重视习题潜在的数学功能、发展功能和教育功能.”教材习题承担着帮助学生理解和掌握数学基本知识、形成和发展数学基本技能的重要功能，特别是一些经典例题、习题是十分有价值的教学资源，也是很多中考题源的根，重视习题的探究学习，能很好地帮助学生整合知识、探索规律、形成方法、获得经验、从而发展学生思维.

1 题目呈现

已知：如图1，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线垂直，垂足为D.

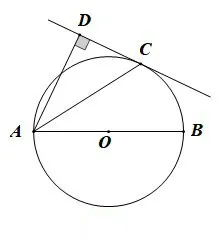
图1

求证：AC平分∠DAB.

本题是沪科版数学九年级下册第24章圆第69页第14 题.题目蕴含丰富的几何关系，比如圆周角定理、切线性质、垂径定理、角平分线性质、弦切角定理、三角形相似、圆内接四边形等，这些内容对锻炼学生的识图能力、辨析能力、推理能力以及转化意识都有重要的作用，正如叶圣陶所说：“教材只是个例子.”作为教师在教学中要依托课本习题，从不同的角度、不同的层面、不同的条件进行拓展研究，挖掘问题本质，强化知识理解与应用，发挥习题最大功效，从而帮助学生跳出“题海”.

2 解法及研究

解如图2，连接OC，则由CD是切线可知OC⊥CD，而CD⊥AD，可得OC∥AD，所以∠DAC=∠ACO,而∠ACO=∠OAC，则∠DAC=∠OAC，即AC平分∠DAB.

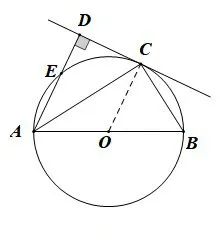
图2

研究1题中三个论断：①CD⊥AD；②CD是⊙O切线；③AC平分∠DAB，知二推一.

研究2相似结构

如图3，连接EC、BC，延长DC交AB延长线于点G.则△DEC∽△DCA,△GBC∽△GCA.

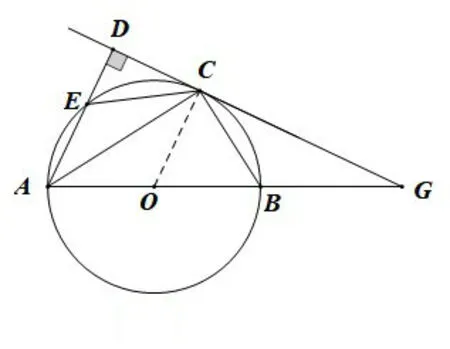
图3

分析由∠BCG+∠OCB=90°,∠AOC+∠OCB=90°，得∠AOC=∠BCG,从而∠CAO=∠BCG,则△GBC∽△GCA；同理△DEC∽△DCA，这里∠BCG、∠DCE为⊙O的弦切角（弦切角等于弦与切线所夹弧所对的圆周角）.

研究3旋转结构

由于AC平分∠DAB，根据圆周角定理可知CB=CE，四边形ABCE为对角互补且有一组邻边相等的特殊四边形.

如图4，过点C作CF⊥AB，根据AC平分∠DAB，知CD=CF，从 而Rt△CDE≌Rt△CFB(HL)（旋转全等）.

图4

如 图5，过 点C作EC垂线，交AD延长线于点H，由圆内接四边形性质可知∠HEC=∠ABC,从 而可得△HCE ≌△ACB(ASA)（旋转全等），则CH=CA,从而可得△CEB∽△CHA（旋转相似）.

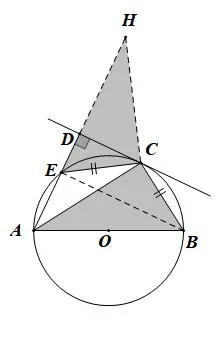
图5

研究4对称结构

如图6，延长BC交AD延长线于点P，过点E作AC的垂线交AB于点Q.由AC平分∠DAB，可得等腰△ABP、等腰△AQE，从而根据等腰三角形三线合一可知点B关于AC的对称点为点P，点E关于AC的对称点为点Q.

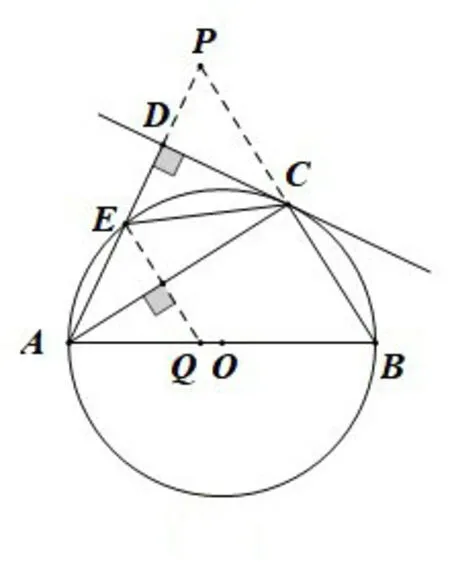
图6

评析课本一道简约的题目蕴含着丰富的几何内涵，在探究中寻找问题的增长点，在平时教学中善于挖掘课本习题，让经典习题的价值最大化，提炼出问题结构本质，使学生通过一道题的探究掌握一类题的解法.

3 考题应用

如 图7，AB是⊙O的直径，C是弧AB上 一点，点P在圆上，连接AP，若AP平分∠CAB,AB=3,AC=1,连接BC、BP，则线段BP的长为.

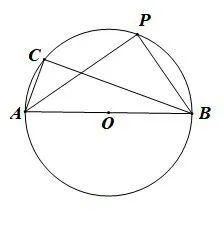
图7

分析根据圆周角定理可知∠ACB=∠APB=90°,由勾股定理可得BC=

如图8，连接PC，由AP平分∠CAB，根据圆周角定理可知PC=PB，连接OP，由垂径定理可知OP垂直平分弦BC，圆内接四边形ABPC为对角互补，且有一邻边相等的四边形.

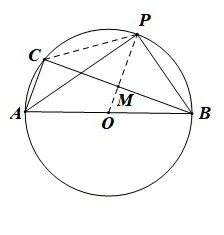
图8

据此分析可得以下精彩解法：

在Rt△BMP中由勾股定理得：BP=

解法2如图9，设AP、BC交于点D，过点D作DE⊥AB，由AP平分∠BAC得DC=DE,可得△DEB∽△ACB，

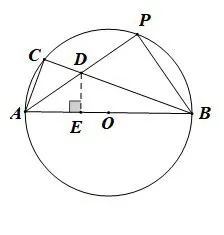
图9

解法3因为AB为直径，从而得∠APB为直角，即AP⊥BP，而AP平分∠BAC，延长AC交BP延长线于点N，如图10，可得AP垂直平分BN，从而得：AN=AB=3.而AC=1，即CN=2，又 因ABPC为圆O的内接四边形，所以∠NCP=∠NBA，

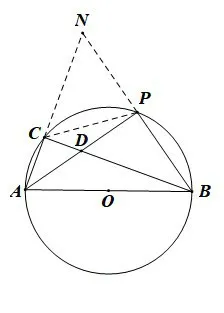
图10

得到△NCP∽△NBA，从而

解得PB=（负值舍去）.

注这里也可以在Rt△NCB中，由勾股定理可得BP=从而PB=

解法4观察目标线段BP所在“环境”——△ABP中，AB=3，考虑求解∠PAB的三角函数值即可计算出线段BP.而∠PAB=∠CAB，如图11，延长CA，在CA的延长线上截取AM=AB，连接BM，由三角形外角可知∠CAB=2∠M，从而∠M=∠PAB.

图11

解法5如图12，过点C作AP垂线于点H，交AB于点G.由AP平分∠CAB，可证△CAH≌△GAH(ASA)，则AG=AC=1,HG=HC.

图12

注此法也可这样处理：如图12-1，将△ACP沿着AP折叠.因为AP平分∠CAB，从而点C的对应点Q落在AB上，则AQ=AC=1,BQ=AB-AQ=2，PQ=PC=PB.

图12-1

过 点P作PM⊥AB，则点M为QB的中点，即BM==1,在Rt△PAB中，射影定理得BP2=BM·BA，即BP=（负值舍去）.

解法6如图13，过点P作AB,AC垂线交AB于点M，交AC的延长线于点N，

图13

由AP平分∠CAB知PN=PM,可证Rt△PNC≌Rt△PMB(HL).

所以NC=MB,AN=AM，解得BM=NC=1,AM=2.

在Rt△PAB中，射影定理得BP2=BM·BA，即BP=（负值舍去）.

也可以这样处理，如图14，延长AB，使得BQ=AC=1，则AQ=AB+BQ=4,

图14

由圆内接四边形性质知∠PBQ=∠DCA,

所以△DCA≌△DBQ()SAS，则PA=PQ,

过点P作PM⊥AQ，则点M为AQ中点，所以

MQ=AQ=2,MB=MQ-BQ=1,

在Rt△PAB中，射影定理得BP2=BM·BA，

即BP=（负值舍去）.

解法7如图15，连接OP，过 点P作OP的垂线，交AB的延长线于点H，由OP⊥PH，可知OP//AC,BC//HP，从 而,可得OH=3OP=则AH=AO+OH=6.

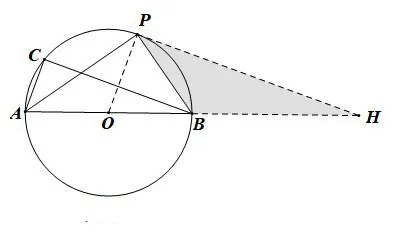
图15

在Rt△OPH中，勾股定理得：

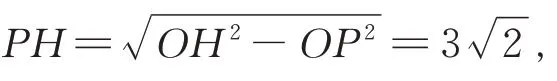
由∠BPH=∠OPA=∠PAO，

所以△BHP∽△PHA，从而

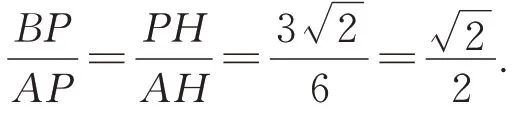
在Rt△DAB中，设BP=a,AD=2a，勾股定理得：AD2+BD2=AB2，解得a=（负值舍去），即BP=

4 思考

落实核心素养的教学目标不再是具体的知识点，而是帮助运用知识解决问题.中考题所运用的知识不局限于一节课的内容，可能是跨章节的，也可能是跨学段的.因此在平时的教学中教师需要提供给学生一定广度的学习资源，从不同视角、不同层面提供素材，以启发学生，全面分析问题，帮助学生解决问题.[1]教材是实现数学课程目标、学生学习的重要资源，教材习题的选题凝聚着编者的智慧与心血，经典习题，思考的角度不同，可得到不同的解答方法，充分挖掘题目的内涵与外延，这样的训练可以拓宽学生的解题思路，调动学生积极性，增强学生学习数学的信心，教师的责任就在于如何设计教学、筛选资源、加工资源，用心帮助学生养成挖掘和研究习题的习惯，力争每一道题目发挥最大的教育功效，让学生脱离“题海”.“双减”之下，教师更要做好“增压”，通过一题多解、一题多变，促进学生思维发展、技能提升、素养提高.