潘全香

(河南工学院 理学部,河南 新乡453003)

0 引言

20世纪80年代,Hamilton提出了Ricci流的概念[1],实际上Ricci流的最初引进是为了解决三维流形著名的Poincarē猜想(任意单连通的三维完备闭流形同胚于三维闭球面)。Ricci孤立子是Ricci流的自相似解且经常出现在Ricci流方程的奇异点经伸缩变换后的极限中。一方面,Ricci孤立子的研究有助于更好地理解Ricci流的奇异结构,从而结合几何手术的方法得到一些重要的几何和拓扑结构;另一方面,Ricci孤立子是爱因斯坦度量的自然推广(也称为quasi-Einstein度量),在规范场论与超弦理论中有重要的应用[2]。因此,Ricci孤立子的几何性质及几何不变量对于数学及物理学的发展均具有重要的研究意义。

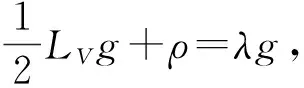
1972年，Kenmotsu研究了一类满足某些特殊条件的切触黎曼流形，即著名的Kenmotsu流形[3]。仿切触流形的重要性主要来自仿Kahler流形的理论。最近几年，随着仿切触度量流形研究的兴起，几何学者开始研究仿Sasaki流形、仿Kenmotsu流形、仿余辛流形上的几何结构。由于在切触几何框架下对Ricci孤立子的研究很有趣且较完善[4-9]，因此，许多几何学者在相关领域继续进行了大量的研究。Calvaruso-Perrone研究了三维近仿切触度量流形上的Ricci 孤立子，并且给出许多例子[10]。Bejan Crassmareanu 研究了三维规范仿切触度量流形上的Ricci孤立子[11]。另外，Blaga研究了仿Kenmotsu流形上的η-Ricci孤立子[12]。受此启发，本文在Ricci recurrent 和φ-recurrent的条件下研究具有Ricci孤立子的仿Kenmotsu流形并给出其分类定理。第一部分给出仿切触度量流形仿Kenmotsu流形的一些概念与结论；第二部分给出Ricci-recurrent 仿Kenmotsu流形的分类定理；第三部分得到φ-recurrent仿Kenmotsu流形的分类定理。

1 仿切触度量流形

这一部分，给出关于仿切触度量流形的一些概念、性质与结论，更多细节与例子参见文献[13]。

设光滑流形M，若它具有(1-1)型张量场φ，向量场ξ，1-形式η满足如下条件：φ2=I-η⊗ξ，φ(ξ)=0，η·φ=0，η(ξ)=1。那么称组合(φ，ξ，η)是一个近仿切触结构，称组合(M，φ，ξ，η)为仿切触度量流形。另外，若存在伪黎曼度量g，使得对任意向量场X，Y，都有g(φX，φY)=-g(X,Y)+η(X)η(Y)成立，称组合(M，φ，ξ，η，g)为仿切触度量流形，此时称g为可容度量。仿切触度量结构上的基本2-形式Φ定义为：Φ(X，Y)=g(X,φY)。若Φ=dη，那么流形(M，φ，ξ，η，g)称为仿切触度量流形。近仿切触度量流形M上，若(∇Xφ)Y=η(Y)φX+g(X,φY)，则称M为仿Kenmotsu流形。

仿Kenmotsu流形上，下列式子成立：

∇Xξ=-X+η(X)ξ

R(X，Y)ξ=η(X)Y-η(Y)X

Qξ=-2nξ

(Lξg)(Y,Z)=-2{g(Y,Z)-η(Y)η(Z)}

命题1 设(g,ξ,λ)是仿Kenmotsu流形M2n+1上的Ricci孤立子，则M2n+1是η-Einstein 流形且r=2n(1+λ)+λ。

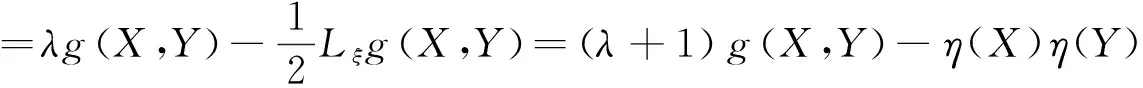
M2n+1是η-Einstein 流形。又由QX=(λ+1)X-η(X)ξ，由数量曲率的定义有

利用与文献[14]类似的方法可得如下引理:

引理1 设(M,g)为φ-recurrent 仿Kenmotsu流形,ξ是特征向量场，A是M上的非零1-形式，α是其对应的向量场，这里A(W)=η(α)η(W)。

2 Ricci-recurrent 仿Kenmotsu流形

定义1 仿Kenmotsu流形M上若存在非零1-形式A，使得

(∇Wρ)(Y,Z)=A(W)ρ(Y,Z)

(1)

则称M为Ricci-recurrent 仿Kenmotsu流形。

这一部分我们考虑Ricci-recurrent 仿Kenmotsu流形M。利用Ricci曲率张量ρ沿任意方向的协变导数为

(∇Wρ)(Y,ξ)=∇Wρ(Y,ξ)-ρ(∇WY,ξ)-ρ(Y,∇Wξ)

在式(1)中令Z=ξ,经过直接的代数计算可得

(∇Wρ)(Y,ξ)=∇Wρ(Y,ξ)-ρ(∇WY,ξ)-ρ(Y,∇Wξ)

=∇W(-2nη(Y))+2ng(∇WY,ξ)+ρ(Y,W-η(X)ξ)

=2ng(W,Y)+ρ(W,Y)

由Ricci-recurrent 仿Kenmotsu流形定义知：

(∇Wρ)(Y,ξ)=A(W)ρ(Y,ξ)=-2nA(W)η(Y)

所以

ρ(W,Y)=-2nA(W)η(Y)-2ng(W,Y)

(2)

在式(2)中令Y=ξ，得

ρ(W,ξ)=-2nA(W)-2nη(W)

令W=ξ，得

λ=ρ(ξ,ξ)=-2nA(ξ)-2n=-2n(A(ξ)+1)

由以上讨论可得：

定理1 设(g,ξ,λ)是Ricci-recurrent仿Kenmotsu流形M2n+1上的Ricci孤立子，A是流形上的1-形式。则当A(ξ)<-1时Ricci孤立子是扩张的。当A(ξ)=-1时Ricci孤立子是稳定的。当A(ξ)>-1时Ricci孤立子是收缩的。

推论1 设(g,ξ,λ)是Ricci-recurrent仿Kenmotsu流形M2n+1上的Ricci孤立子，若1-形式A=η，则M2n+1是η-Einstein流形，且此时a=b=-2n。

3 φ-recurrent仿Kenmotsu流形

定义2 仿Kenmotsu流形M上若存在非零1-形式A，使得对任意切向量场X,Y,Z,W满足

φ2((∇WR)(X,Y)Z)=A(W)R(X,Y)Z

(3)

则称M为φ-recurrent 仿Kenmotsu流形。

设M为φ-recurrent 仿Kenmotsu流形，由定义可得：

(∇WR)(X,Y)Z-η((∇WR)(X,Y)Z)ξ=A(W)R(X,Y)Z

(4)

上式与U做内积得

g((∇WR)(X,Y)Z,U)-η((∇WR)(X,Y)Z)η(U)=A(W)g(R(X,Y)Z,U)

(5)

设{ei}(i=1,…,2n+1)是流形上任一点的切空间上的一组平行规范基。在式(5)中取X=U=ei并关于i求和，容易得到

(∇Wρ)(Y,Z)=A(W)ρ(Y,Z)

(6)

在式(6)中用ξ代替Z且利用式(1)，有

(∇Wρ)(Y,ξ)=-2nA(W)η(Y)

(7)

又

(∇Wρ)(Y,ξ)=∇Wρ(Y,ξ)-ρ(∇WY,ξ)-ρ(Y,∇Wξ)=2ng(W,Y)+ρ(W,Y)

所以

ρ(W,Y)=-2nA(W)η(Y)-2ng(W,Y)

(8)

综上讨论可得：

定理2 设(g,ξ,λ)是φ-recurrent仿Kenmotsu流形M2n+1上的Ricci孤立子，A是流形上的1-形式，则当A(ξ)<-1时Ricci孤立子是扩张的，当A(ξ)=-1时Ricci孤立子是稳定的，当A(ξ)>-1时Ricci孤立子是收缩的。

推论2 设(g,ξ,λ)是φ-recurrent仿Kenmotsu流形M2n+1上的Ricci孤立子，若1-形式A=η，则M2n+1是η-Einstein流形，且此时a=b=-2n。