北京市第十二中学高中部(100071) 赵 毅 刘 刚

1 问题提出

题目已知椭圆=1(a >b >0),点(1,e)和都在椭圆E上,其中e为椭圆E的离心率.

(1)求椭圆E的方程;

(2) 如图1,设椭圆E的左、右顶点分别为A、B,过点P(−2,2) 的直线l与椭圆E分别交于点M、N,直线OP与BM交于点Q,求证:AQ//BN.

图1

试题考查了椭圆的标准方程、几何性质、直线与椭圆的位置关系以及两条直线平行问题,考查了直观想象、逻辑推理、数学运算等核心素养.试题构思巧妙,解法多样,内涵丰富,是一道具有研究性学习价值的好题.第(1)问求得椭圆E的方程为+y2=1,下面探究一下第(2)问的证法以及推广,供大家参考.

2 证法探究

点评两种证法都是把证明两条直线平行问题转化为证明它们的斜率相等,证法1 借助点M,N的坐标表示出AQ,BN的斜率,然后联立直线l与椭圆E的方程并根据韦达定理解决;证法2 借助椭圆的参数方程设出点M,N的坐标,然后借助三角公式解决.两种证法体现了坐标法的应用.

3 推广探究

将试题一般化,得到:

性质1 已知椭圆=1(a >b >0)的左、右顶点分别为A,B,过点P(−a,a)的直线l与椭圆E分别交于点M、N,直线OP与BM交于点Q,则AQ//BN.

由于直线AP与椭圆E相切,将点P改为直线x=−a上任一点,有:

性质2 已知椭圆=1(a >b >0)的左、右顶点分别为A,B,过点P(−a,m)(m ∈R,且0)的直线l与椭圆E分别交于点M、N,直线OP与BM交于点Q,则AQ//BN.

若P是椭圆E外任一点,则有:

性质3 如图2,已知椭圆=1(a >b >0)外一点P,直线PA与椭圆E相切于点A,点A关于原点O的对称点为B,过点P的直线l与椭圆E分别交于点M、N,直线OP与BM交于点Q,则AQ//BN.

图2

由椭圆类比圆,双曲线,有以下性质.

性质4 已知圆O外一点P,直线PA与圆O相切于点A,点A关于圆心O的对称点为B,过点P的直线l与圆O分别交于点M、N,直线OP与BM交于点Q,则AQ//BN.

证法1 如图3,过P作圆O的另外一条切线PC,切点为C,延长PO与BN交于点D,连接CM,CA,CQ,CN,CD,AD,因为PA是圆O的切线,所以OP⊥AC.由已知可得AB是圆O的直径,所以AC⊥BC,由此得OP//BC,于是∠PQM=∠DQB=∠QBC=∠PCM,所以P,M,Q,C四点共圆.同理,P,N,D,C四点共圆,所以∠MCQ=∠MPQ=∠NPD=∠NCD,于是∠QCD=∠MCN=∠MBN=∠QBD,所以Q,D,B,C四点共圆,所以四边形QDBC是等腰梯形,由此得QO=OD,于是四边形ADBQ是平行四边形,故AQ//BN.

图3

证法2 如图4,过P作圆O的另外一条切线PC,切点为C,延长PO与BN交于点D,连接AC,AD,因为PA,PC是圆O的切线,A,C为切点,且PMN是圆O的割线,所以M,A,N,C是调和四边形的四个顶点.又B在圆O上,所以BC,BM,BA,BN是调和线束.由证法1 可得OP//BC,所以QO=OD,于是四边形ADBQ是平行四边形,故AQ//BN.

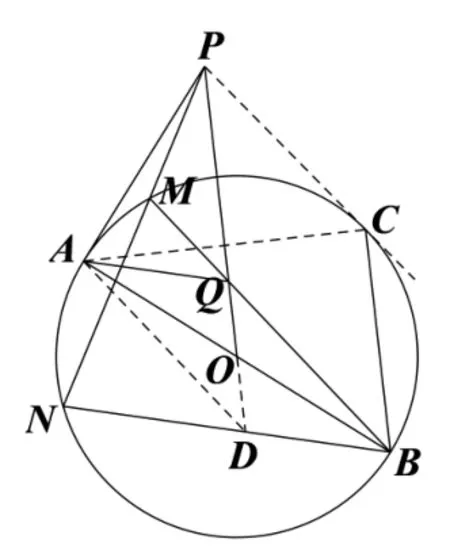
图4

性质5 已知双曲线=1(a>0,b>0)外一点P,直线PA与双曲线E相切于点A,点A关于原点O的对称点为B,过点P的直线l与双曲线E分别交于点M、N,直线OP与BM交于点Q,则AQ//BN.