广东省广州市执信中学(510080) 尧禄华

1 引言

逻辑推理素养是《普通高中数学标准(2017 年版)》中明确规定的六大核心素养之一,对学生成长具有重要意义,在形成人的科学严谨、理性思维及促进学生全面发展具有重要作用.2017 版课程标准指出:逻辑推理是指从一些事实和命题出发,依据规则推出其它命题的素养.

相比之前的阶段学习,高中是学生逻辑推理能力发展的重要阶段,需要更强的逻辑推理能力.学生通过高中课程学习,要掌握基本的逻辑推理形式,要有逻辑的思考问题,要能够在比较复杂的情境中把握事物之间的关联,把握事物的发展脉络,形成重论据、有条理、合乎逻辑的思维品质和理性精神,增强交流能力.因此,在高中课堂教学中培养学生的逻辑推理能力显得更为重要.

众所周知,解题教学历来是提升学生思维能力、培养和发展学生核心素养的重要途径.教师可以通过典型的、具体的题目,引导学生开展探究活动,帮助学生理解数学知识,构建知识内在逻辑,合理得出数学结论,体会蕴含其中的数学思想方法,培养学生的逻辑推理素养.

目前关于如何培养学生逻辑推理素养,已经有很多文献给出了很好的建议.但主要聚焦于新授课中,例如文献1、2、3;也有的是从教材编写角度,阐述编者意图,培养学生逻辑推理素养,例如文献4.但是对于如何在解题中培养学生逻辑推理素养,却鲜有论述.2021 年全国卷第17 题是一道数列知识的题,考查的知识是数列奇偶项分类,数列通项、求和等.对于类似题目,备考中学生做过不少练习,在各类模拟试卷中也经常出现,对大部分学生而言是必须要拿到一个满意分数.然而从阅卷老师反馈得知,得分并不乐观;尤其是第二问,从教师角度看,就算逐项计算,得出前20 项的和也并不困难,然而很多学生却没有计算正确结果,甚至不少交空白卷.为什么大量练习失效了,难道是“熟能生笨”.数列作为每年高考重点,承载着命题者对多种核心素养的考查,抛开学生运算能力不足、步骤不严谨丢分原因之外,另一个原因便是学生思维不够灵活、逻辑推理素养不高.据此,下文笔者以一道平常数列问题的解决为例,通过变式与拓展,逐步开拓学生思路,引导学生深度思考,从本质上把握问题,培养学生逻辑推理素养,提高学生解决问题能力.

2 一道数列题的教学过程

题目:已知数列{an}中,a1=1,an+an+1=n2,n ∈N*,求数列{an}通项.

实践教学表明,学生在第一次接触该题目时,会感觉到无从下手.如果直接告诉怎样解答,则学生感觉无异于魔术师从帽子里变出一只兔子来,下次碰到类似问题,还是不会解决.

2.1 从学生最近发展区设计教学,培养前后连贯一致的逻辑思维

要构建前后连贯一致的逻辑推理,首先要具备逻辑思维的起点.即面对一个新问题,我们应该先找到问题突破口,从而进行逻辑推理,推动解题向目标前进.通常情况下,问题的突破口隐藏在学生已有的认知经验中.但实际解题中,某些问题思维跨度较大,或者情境较为陌生,学生是不容易根据已有经验想到的;这时,就需要教师精心设计问题串,合理搭建台阶,从学生最近发展区开展教学,让学生思维自然流淌,从而构建出从已知条件到问题(结论)的前后连贯一致的逻辑推理,从而提高学生有逻辑的分析问题能力.

考虑到学生已有的认知基础,对等差数列很熟悉,本题可以设计如下问题串:

问题1:如果把条件“an+an+1=2,n ∈N*”改为:“an+1-an=2,n ∈N*”,大家熟悉吗?

这是一个等差数列题,学生当然熟悉.进一步追问:

问题2:如果改为“an+1-an=2n-1,n ∈N*”,能求出数列{an}通项吗?

这仍然是学生熟悉的问题,稍加思索,学生便能够想到运用累加法.不过需要提醒学生注意数列的角标问题.

问题3:如果改为“Sn-an=n2,n ∈N*”,能求出数列{an}通项吗?

这是一个已知Sn与an关系,求数列通项的问题,学生也能很快想到运用公式an=,求出{an}通项.需要提醒学生注意的是,运用该公式能推出的通项公式仅当n≥2 成立,需要检验a1的数值是否满足这个通项.

问题4:如果把条件改为“a1=1,a2=2,an+2-an=2,n ∈N*”,求数列{an}通项.

对于该问题,学生第一感觉这好像是一个等差数列,但又有所区别.这并不是连续相邻两项的差是一个常数,而是中间隔了一项的“相邻”的两项的差是一个常数,也即是该数列的奇数项、偶数项分别成等差数列;此时,只需要引导学生用数学符号表达即可.由a2k-1=a1+(k-1)d=2k-1,a2k=a2+(k-1)d=2k得,an=n,n ∈N*.

通过以上四个问题,不难发现一个共性,就是要顺利求出某个数列通项,关键在于能否把已知条件转化成“类等差”数列的结构.例如an-an-1=f(n)、an-Aan-1=f(n)、an+2-an=f(n)等结构,其中f(n)可以是常数C、c·n+d、或者C ·an等.这种转化是符合学生认知基础的,把一个未知问题,转化成曾经学过的、熟悉的、已经解决了的问题.

回到开头提出的问题,条件是an+an+1=n2,n ∈N*,等式左边是两项相邻的和,那么如何才能转化成上述“类等差”数列的结构呢? 这是解决本题的关键.思索片刻后,学生有下面解法:

仿照问题3 的处理方法,由an+an+1=n2,n ∈N*,可得an+1+an+2=(n+1)2,n ∈N*,两式相减得an+2-an=(n+1)2-n2=2n+1,由累加法可得，

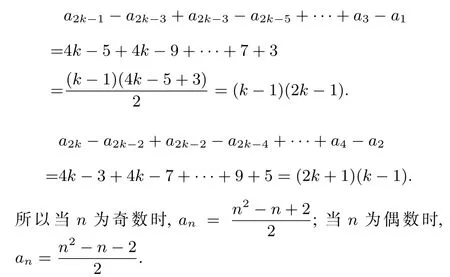
以上的教学设计充分揭示了解题思维的形成过程,相比直接告诉学生解法,更能让学生理解老师“是怎么想到的”,也即知其然,更知其所以然.

2.2 多角度构建知识间的联系,培养学生思维广阔性

著名特级教师孙维刚曾说:教师要站在系统的高度教学,使学生对知识产生八方联系,渐渐使学生思维养成时时处在浮想联翩、思潮如涌的状态.就本题而言,进一步观察“an+an+1=n2,n ∈N*”结构特征,不难发现,这是一个相邻的两项和结构,那么我们完全可以推出数列{an}的前n项和Sn,再通过Sn求出an.

解法2:当n为偶数时,

再比如学生在平常练习中经常会出现把“an+1=A·an+B”转化成“an+1+p=A·(an+p)”结构,如果从这个角度考虑,是否也可以得出答案呢? 答案显然是肯定的.

2.3 适度变式训练,培养学生归纳、类比能力

教师在课堂教学中,要善于抓住教学契机,引导学生加强知识、解题方法纵横间联系,适度进行变式教学,培养学生归纳、类比能力,解题方法迁移能力.章建跃博士在文5 中曾说道:“变式”对于揭露数学知识的本质和思想方法具有重要意义,可以使“再发现”的过程既简约又有效,使数学知识各侧面的本质特征更加显露突出,有利于学生“透过现象看本质”,使学生更容易地发现“变化中的不变性”“变化中的规律性”,在形式的运动变化过程中认识内容,体验数学研究的过程、数学思想方法的真谛.就本题,至少可以从以下几个方面引导学生变式拓展,加深对解题方法、思路的深刻理解,进一步把握问题的本质.

改变等式“an+an+1=n2”的右边:

变式1:已知数列{an}中,a1=1,,求数列an+an+1=n2+n,n ∈N*通项.

变式2:已知数列{an}中,a1=1,an+an+1=an,n ∈N*,求数列{an}通项.

上述变式主要拘泥于转化成“类等差”数列结构.若从训练学生知识迁移、类比能力角度考虑,本题也可以设计一些转化成“类等比”数列结构的问题.

改变等式“an+an+1=n2”的左边;

变式3:已 知 数列{an}中,a1=1,an · an+1=n(n+1),n ∈N*,求数列通项.

变式4:已知数列{an}中,a1=1,an·an+1=an,n ∈N*,求数列{an}通项.

事实上,学生掌握情况良好,我们还可以提出更高的要求,设计一些开放性的问题,进一步促进学生深度思考,理解问题的本质.

变式5:已知数列{an}中,a1=1,an+an+1=f(n),n ∈N*,其中f(n) 需要满足什么样的表达式,能求数列{an}通项.你能列举几个吗?

变式6:已知数列{an}中,a1=1,an·an+1=f(n),n ∈N*,其中f(n)需要满足什么样的表达式,能求数列{an}通项.你能列举几个吗?

上述变式产生是自然的、合理的,它不同于简单的应试训练,而是基于数学发展内在的变与不变,基于学生认知发展和素养生成的规律,一方面加深了学生对问题的理解,另一方面也提升了数学运算和逻辑推理等核心素养.是学生易于接受的.

3 结束语

适当类似重复题型训练是可以有效增加学生解题经验和熟练度,也可以提高类似题型的解题速度.但是如果忽略解题过程中逻辑推理能力的培养,盲目的加大训练量,压榨学生时间,普通学生也只能是机械式的记忆,简单的模仿,将事倍功半.特别是在面对承载着考察核心素养的新高考试题中,反复训练将会越来越难以凑效.从长远来看,反复训练也会降低学生创造性能力和对问题理解力.教师要充分研究《课程标准》,准确理解新课程理念,充分挖掘教学资源,在遵循学生认知基础上,适当的带领学生进行变式拓展训练,多角度思考问题,激发学生深度思考,培养学生核心素养.