扬州大学数学科学学院(225000) 王张毅

1 问题提出

二次函数是初中数学的教学重点,也是许多地区中考的热门考点,同时作为初中、高中阶段的重要衔接部分,二次函数既是初中函数学习的难点,又是高中函数学习的重要工具.

一直以来各地中考对于二次函数的要求都较高,对二次函数的考察也比较灵活与综合,不仅考察二次函数性质、图像,还常与其它知识结合来综合考察学生的思维与应用能力.

中考是高中选拔学生的重要依据,学生只有顺利通过中考才有机会接受更高层次的教育,而压轴题具有较大的难度与区分度,对于学生的考试成绩至关重要,因此如何顺利解出压轴题是一个重要的课题.压轴题的题型多变,涉及的知识点复杂,其中以二次函数为知识背景的压轴题出现频率较高.

由于中考对二次函数考察的复杂性以及问题结论的多样性,往往需要运用分类讨论的思想方法对问题的因素进行分类.分类讨论思想方法是依据数学问题的本质属性,将其划分为若干不同种类,然后逐类研究,是解决此类复杂问题的有效工具.

2 分类讨论思想

分类讨论思想是依据一定的原则与标准,将所要研究的数学对象划分为若干种不同的情形,再分别对每一种情形进行讨论的数学思想.分类讨论思想对于简化复杂问题、厘清研究思路起着重要的作用.

分类讨论的基本步骤是:(1)明确分类对象(2)确立分类依据(3)合理实施分类(4)逐类分析讨论(5)归纳总结.分类讨论一般要满足不重复、不遗漏、分类标准统一等原则.

上述关于分类讨论思想的讨论可以用以下数学语言表述:

若要证明命题Q对于集合I成立,只要将集合I分为若干个子集Ii(i=1,2,3,...,n),且满足I1∪I2∪I3∪...∪In=I,I1∩I2∩I3∩...∩In=ϕ,再证明命题Q对于Ii(i=1,2,3,...,n)都成立,则命题Q对于集合I成立.

3 例题分析

3.1 与二次函数图像和对称轴上的动点有关的分类

例1 (2020·宿迁·28)二次函数y=ax2+bx+3 的图象与x轴交于A(2,0),B(6,0)两点,与y轴交于点C,顶点为E.

(1)求这个二次函数的表达式,并写出点E的坐标;

(2)如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;

(3) 如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当ΔCQE的面积为12 时,求点P的坐标.

图1

分析:第(2)问中的点D与第(3)问中的点P都是动点,动点问题往往采用静态化的处理策略,也就是在运动过程中选取某一静止状态下的特殊情形来代表某一连续状态,通过对具有代表性的静止状态的分析可以掌握连续状态下的整体性质,以完成动点问题的求解,因此选取合适的静止状态成为解决动点问题的突破口.

如何选取合适的静止状态? 首先就要在分类讨论思想的指导下对动点的整个运动状态进行分类,其中的关键就是找到运动状态中不同情形的分界点.如本题的第(2)问,将“BD的垂直平分线恰好经过点C”这一条件转化为“CB=CD”后,实际上该问题就变成“当二次函数对称轴上的点D运动到何处时,CB=CD”,考虑点D的整个运动过程,可以划分为点D在线段BC上方与下方两种情况,将点D这一动态过程划分为两个动态过程,再静态化处理画出两个动态过程下满足CB=CD这一条件的草图,充分考虑这两种情况后再结合几何特性与代数方法,该问题就可以顺利解决.而题目中给出的图只包含点D在线段BC上方一种情况,如果不在分类讨论思想的指导下,可能就会导致该问题的漏解.

第(3)问是由于点P的运动而导致ΔCQE的形状在变化,这就意味着在点P的运动过程中ΔCQE的面积也在不断变化.考虑点P运动到何处时满足ΔCQE的面积为12,思路自然是引入参数表示点P的坐标从而得到点Q的坐标,再利用几何性质用参数表示ΔCQE的面积,通过求解方程即可解决本题.但由于在运动过程中ΔCQE的形状在不断改变,其几何特征也在变化,所以要将动态过程静态化,找到具有代表性的静止状态下的ΔCQE的形状,分析其几何特征才能顺利列出方程.在分类讨论的思想指导下,考虑点P的整个运动过程,不难发现点C、E为运动状态的分界点,即可以将整个运动状态分为点P在点C左边、点P在点C与点E之间、点P在点C右边三种情形,然后再画出草图分别考虑三种情形下ΔCQE的几何特征,该题便可游刃而解.

例2 (2020 ·常州市· 28) 如图,二次函数y=x2+bx+3 的图像与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点C(1,0),且顶点为D,连接AC、BC、BD、CD.

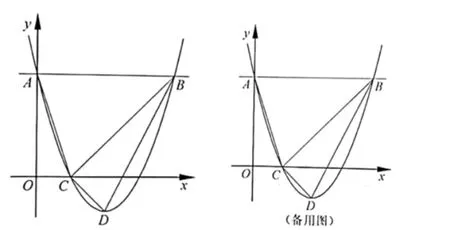
图2

(1)填空:b=____;

(2)点P是抛物线上一点,点P的横坐标大于1,直线PC交直线BD于点Q.若∠CQD=∠ACB,求点P的坐标;

(3)点E在直线AC上,点E关于直线BD对称的点为F,点F关于直线BC对称的点为G,连接AG.当点F在x轴上时,直接写出AG的长.

分析:本题是一道难度较大的中考压轴题,实际上与例1 同样属于动点问题,不少学生难以下手,但是在分类讨论思想的指导下,将动点问题静态化处理,第(2)问的解题难度会陡然下降.

题目中的∠ACB的大小是确定的,∠CQD的大小因为点Q的运动而不确定,考虑点Q的整个运动过程与点P相关,假设点P从左往右运动,不难发现∠CQD的度数存在先增大再减小的过程,所以可将整个运动过程一分为二,由此可知应该至少有两种情况满足题目要求,再分别考虑两种情况下的图形的几何特性进行求解,该题的难度大大降低,在解题时能够有路可走.

3.2 与二次函数图像中直角三角形有关的分类

例3 (2020·无锡·17)二次函数y=ax2-3ax+3的图像过点A(6,0),且与y轴交于点B,点M在该抛物线的对称轴上,若ΔABM是以AB为直角边的直角三角形,则点M的坐标为_____.

分析:本题中只给出边AB是直角边,而一个直角三角形中有两条直角边,现在根据边AB是直角边这一条件可以确定边AB对应的∠AMB一定不是直角,但剩下的∠AMB与∠BAM都有可能是直角,因此在分类讨论的思想下指导,该题的解答思路会更加清晰.

在ΔABM中A,B两点为定点,点M在对称轴上,两种情况在图像上的分界点应该是AB与对称轴的交点,所以一种情况是点M在这个交点的上方,另一种情况是点M在这个交点的下方,根据分类的情况各自画出草图,再利用图形之间的几何关系就可以解答本题,所以求解本题的关键就是找到分类讨论的依据进行合理分类.

例4 (2020·盐城·25)若二次函数y=ax2+bx+c的图像与x轴有两个交点M(x1,0),N(x2,0)(0＜x1＜x2),且经过点A(0,2) 过点A的直线l与x轴交于点C,与该函数的图像交于点B(异于点A) .满足ΔACN是等腰直角三角形,记ΔAMN的面积为S1,ΔBMN的面积为S2,且

图3

(1)抛物线的开口方向____(填“上”或“下”);

(2)求直线l相应的函数表达式;

(3)求该二次函数的表达式.

分析:本题与例3 一样都是与直角三角形中直角的不确定有关的分类,但是因为直接的限制条件比例3 中更加少,所以在本题中ΔACN的三个角都有可能是直角,因此在完成本题第(2)问时需要分三种情况讨论.在对每种情况单独分析后可以发现其中两种情况可以舍去,最后只剩下一种情况可以求解,所以实际上本题中存在隐藏的限制条件,导致本题中满足要求的只有一种情况.

在用分类讨论思想方法时,要注意所分的每一种情况都需要满足题目中的条件,对于不满足条件的情况讨论后可以舍去,所以对于复杂的问题可以使用分类讨论的思想方法进行简化,在对每一种分类情况逐类讨论时也更加有条理,避免逻辑与思路上的混乱,以提高解题的效率与正确率.

4 小结

由于二次函数的代数与几何性质特征明显,易与其它知识模块产生联系,常常出现在中考压轴题中.从上述例题可以看出,这些考题的难度较大,大多处于中档题与难题的区间,所涉及的题目条件复杂,不少考生往往难以下手.对于其中的一些题目,分类讨论思想方法是极其有效的工具,若在解题过程中合理使用分类讨论,往往会将复杂的问题简化,使解答过程更加条理清晰,也可避免漏解、少解,有助于学生厘清思路,从而达到事半功倍的效果.在使用分类讨论思想方法的过程中一定要先认识讨论对象的全域再确立合适的分类依据,然后进行合理的分类,要保证分类不重不漏,在分类后要对每一个分类进行逐类讨论,最后再将各类情况归纳总结.