苏艳军

(中国建筑东北设计研究院有限公司，沈阳 110166)

1 研究背景

在与岩体相关的工程结构领域中，往往会研究预测岩石的长期变形和强度，为工程结构长期稳定性的把控提供一定参考[1-2]。蠕变本构模型作为一种不断进步和发展的材料变形破坏模拟手段，是岩石蠕变特性研究中的核心内容[3-4]。

国内外对于岩石蠕变本构关系的研究已有较多成果，Moghadam等[5]以盐岩为研究对象，建立黏弹塑性蠕变本构模型，提出一个非线性黏滞系数的牛顿体，构建一个新的非线性黏弹塑性蠕变模型；Günther等[6]探究盐岩稳态蠕变速率与温度及应力之间的联系，构建了不同温度、应力条件下的盐岩蠕变模型；王艳春等[7]进行页岩在不同温度和pH值下的蠕变试验，建立同时考虑温度和pH值的蠕变本构模型；黄方勇[8]在西原模型的基础上，引入分数阶微积分理论，建立改进后的分数阶蠕变模型；张玉等[9]在传统Burgers模型的基础上，引入损伤力学理论，建立改进Burgers蠕变损伤模型；金俊超等[10]通过探索岩石峰后应变软化指标与塑性变形之间的关系，构建一个基于应变软化指标的黏塑性体，与Burgers模型串联得到新的非线性蠕变模型；张亮亮等[11]在广义Burgers模型的基础上，串联一个具有非定常特征的黏塑性元件，得到一个能较好描述砂岩蠕变特征的本构模型。

本文将Maxwell模型和黏塑性体串联，得到结构形式简练的基础模型。采用连续损伤理论，根据能量损伤方式定义损伤变量，构建考虑时效损伤的弹性体来反映岩石弹性应变。引入分数阶微积分理论，得到分数阶软体元件来描述岩石黏弹性应变。为表征黏塑性应变，在分数阶软体元件基础上进行损伤演化，得到考虑时效损伤的分数阶黏塑性体。将改进后的元件代入基础模型，得到考虑时效损伤的岩石分数阶蠕变本构模型，给出参数解析方法，利用泥质板岩蠕变数据验证模型合理性和优越性。探究损伤发展过程，分析参数敏感度，并通过红砂岩、千枚岩单轴压缩各向异性蠕变特性试验数据来验证模型适用性。

2 基础模型及考虑时效损伤的弹性体

2.1 岩石蠕变特征及基础模型择取

大量试验研究表明，不同应力状态下岩石蠕变特征可归纳为图1中的3类曲线[12]，其中曲线①、②均只有衰减和稳定蠕变2个阶段，不同之处在于应力σ与长期强度σp的相对大小。曲线①的应力条件为σ≤σp，稳定蠕变阶段速率为0；曲线②的应力条件为σ>σp，稳定蠕变阶段速率为某一常数。曲线③在曲线②的基础上，还出现了加速蠕变阶段。t1和t2分别为衰减、稳定和加速蠕变阶段的分界时间点，t3为加速蠕变阶段止点。

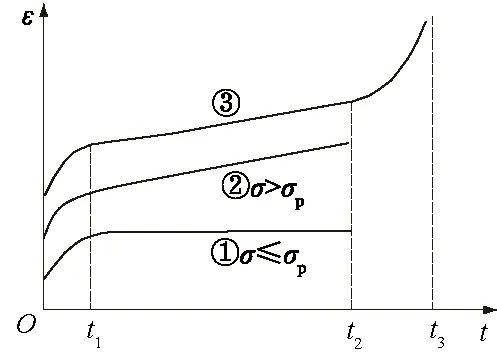
图1 蠕变特征示意图Fig.1 Creep characteristic curves

从图1可知：岩石内部同时赋存着黏弹塑性变形特征，由此模型中须同时含有弹簧体、牛顿体和塑性体。目前多数改进后的蠕变本构模型尽管能取得较好的拟合效果，但是通常存在参数众多、物理意义不明确的缺陷。本文将Maxwell模型和黏塑性元件串联，得到一个结构简单、形式简练的元件模型(图2)，将该模型作为基础模型进行改进，以期得到较为全面、简练的蠕变本构模型。

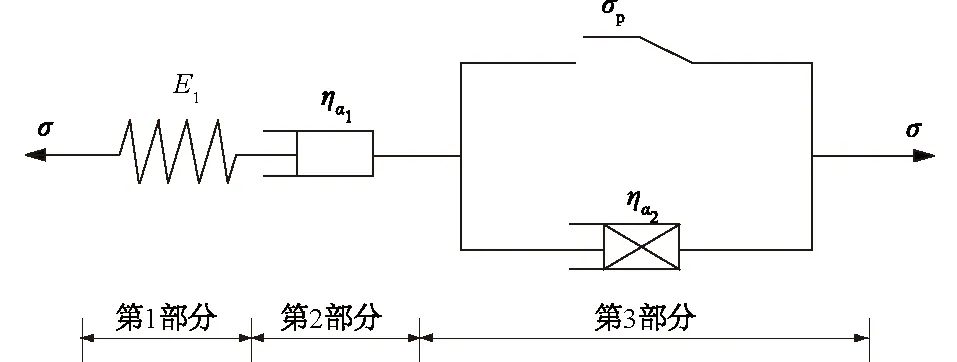
图2 元件模型示意图Fig.2 Model components

该元件模型的蠕变方程为

(1)

式中：σ为应力；E1为瞬时弹性模量；ηα1和ηα2分别为模型第2、第3部分的黏滞系数；α1、α2分别为模型第2、第3部分黏滞体的阶数；ε为模型总应变；t为时间；σp为长期强度。

2.2 损伤变量定义

岩石在外界应力、温度、风化、水等因素的作用下，内部微裂纹发育、扩展和贯通，造成岩石性能劣化的微结构变化即为损伤[9,13]。由此在图2模型的基础上引入连续损伤理论，目前主要有几何损伤和能量损伤2种方式定义损伤变量[13]，前者需测定结构有效承载面积，后者基于弹性模量变化规律。考虑到可操作性，采取能量损伤方式定义损伤变量D(t)。

研究表明，岩石蠕变变形过程中的弹性模量和黏滞系数往往随时间的增长而减小[13]，许宏发[14]进行泥质板岩单轴压缩蠕变试验，得到蠕变变形过程中不同时刻的弹性模量，如表1所示。

表1中弹性模量随着时间增长而递减，时间超过100 d以后，衰减幅度明显放缓。依据表1，通过能量损伤的方法作如下定义：①当t=0时，D(t)=

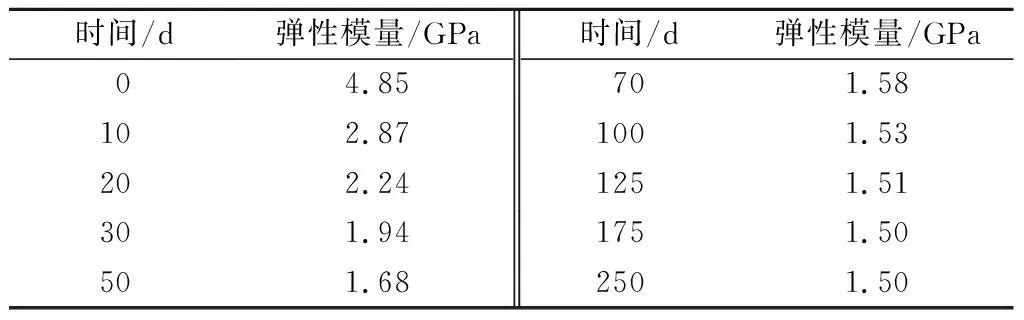
表1 不同时间的弹性模量Table 1 Elastic modulus with time

0；②当t→∞时，D(t)=1；③当t∈(0,∞)时，D(t)随时间增长逐渐趋于1。考虑到弹性模型的衰减规律，由此建立如下负指数型损伤演化方程，即

D(t)=1-e-bt。

(2)

式中b为与岩石损伤相关的参数。

2.3 考虑时效损伤的弹性体

假设岩石材料为各向同性损伤，则弹性模量随时间的损伤劣化可表示为

E(t)=E1[1-D(t)] 。

(3)

式中E(t)为随时间变化的弹性模量。

当加载应力大于长期强度时，岩石内部损伤才开始发展累积[9,13]。无损状态下的岩石对加载应力的响应是瞬时的，通过Hooke体描述弹性应变，即

(4)

式中ε1为改进后模型中第1部分的应变。

当加载应力超过长期强度时，依据Lemaitre[15]等效应变原理有

(5)

式(5)即为考虑时效损伤的弹性体的本构方程。取瞬时弹性模量E1=4.85 GPa，b=1×10-4，可得表1弹性模量衰减规律的拟合曲线，如图3所示。

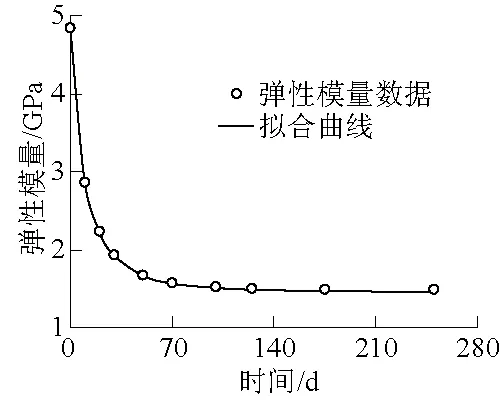
图3 弹性模量拟合曲线Fig.3 Fitted curve of elastic modulus

由图3可知，式(5)能较好地描述弹性模量衰减规律，将考虑时效损伤的弹性体替换基础元件模型第1部分的弹簧体是可行的。

3 基于分数阶微积分的黏滞体和黏塑性体

3.1 Riemann-Liouville型分数阶微积分

分数阶微积分区别于传统整数阶微积分之处在于阶数可为有理分数、无理数甚至复数。分数阶微积分物理意义清晰，形式简练，能较好地描述非线性动力行为，故将其引入来表征岩石蠕变的非线性非定常特征[16]。分数阶微积分根据时域的不同有Caputo型、Grunwald-Letnikov型、Riemann-Liouville型[16]。其中，Riemann-Liouville型相对简练，应用较广。函数f(t)在可积区间[0，t]的α(α>0)阶Riemann-Liouville积分定义为

(6)

式中：f(t)为在可积区间[0，t]的某一函数；α为阶数；s为用于Laplace变换的某一自变量；Γ(α)为Gamma函数，定义为

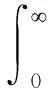
(7)

与积分相对应，函数f(t)的α阶微分定义为

(8)

式中n=[α]。

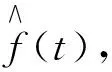
(9)

3.2 基于分数阶微积分的软体元件

岩石材料是一种复杂的非线性材料，其性质被认为是介于理想固体和理想流体之间的某种状态，根据牛顿体本构方程的结构特点，参考Blair[17]引入一种描述该状态的软体元件，其本构方程为

(10)

式中：ε(t)为软体元件的应变；ηα为该软体元件中的黏滞系数。当α=0时，该软体元件可描述理想固体；当α=1时，该软体元件退化为牛顿体；由此认为当α∈(0，1)时，该软体元件可描述介于理想固体和理想流体之间的某种状态。

当应力σ为恒定不变时，依据Riemann-Liouville分数阶微积分算子理论，对式(10)进行分数阶积分得

(11)

式(11)即为基于分数阶微积分的软体元件。

取σ=4 MPa，ηα1=0.5 GPa·d，依据式(11)得到不同α取值对应的蠕变曲线，如图4所示。

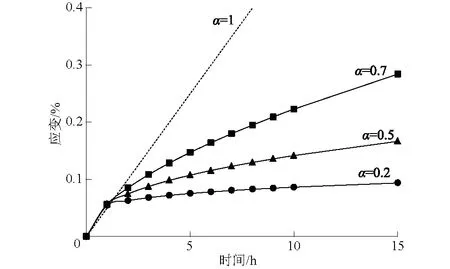
图4 分数阶软体元件蠕变曲线Fig.4 Creep curves of fractional software elements

由图4可看出，当α在区间[0，1]内取不同量值，蠕变曲线表现出不同程度的非线性特征，随着α值的减小，蠕变曲线的非线性特征愈加明显。

3.3 分数阶黏滞体

图4中蠕变曲线随着α值的改变而不断在某个范围内变化，能模拟图1中的曲线①、②，由此说明该软体元件能较好地反映岩石衰减、稳定蠕变阶段。鉴于该软体元件具备描述岩石衰减、稳定蠕变行为的灵活性，将该软体元件替换基础元件模型(图2)中第2部分的牛顿体，利用其描述岩石蠕变黏弹性变形，于是有

(12)

式中ε2为改进后模型中第2部分的应变。

3.4 考虑时效损伤的分数阶黏塑性体

根据图1曲线③可看出，在加速蠕变阶段中曲线斜率不断变化，岩石的黏滞系数将不再恒为常数，而软体元件的黏滞系数是恒定的，故其无法描述岩石加速蠕变行为。因此采用连续损伤理论，依据Lemaitre[15]应变等价性假说，通过损伤变量D(t)来描述黏塑性体黏滞系数的劣化，将软体元件的本构方程写为式(13)。需注意的是，当应力水平超过了长期强度，损伤分数阶黏塑性体才会表现有黏塑性变形，由此应将σ替换成(σ-σp)，即

(13)

式中ε3为改进后模型中第3部分的应变。

将式(2)代入式(13)可得

(14)

式中ηα2e-bt即为黏塑性体中随时间劣化的黏滞系数。

当σ为恒定不变时，依据Riemann-Liouville分数阶微积分算子理论，对式(14)进行分数阶积分得

(15)

式中k表示数学求和符号的下界。式(15)即为考虑时效损伤的分数阶黏塑性体的本构方程。

3.5 考虑时效损伤的岩石分数阶蠕变本构模型

将分数阶黏滞体、考虑时效损伤的弹性体和分数阶黏塑性体串联，参考基础元件模型的组合方式得到

式(16)即为本文考虑时效损伤的岩石分数阶蠕变本构模型。

4 模型验证及参数求解

4.1 参数求取方法

瞬时弹性模量E1取0 d时刻的4.85 GPa，式(16)第一式中的参数ηα1和α1通过一般的非线性最小二乘法便可拟合求解。由于式(16)第二式包含了∑符号，一般的非线性求解方法不适用，故采用双参数的Mittag-Leffler函数[18]进行模型表述，其中该函数表达式为

(17)

式中ω、n和z均为Mittag-Leffler函数的反演计算参数，其中ω>0、n>0、z为常数。

当ω=1时，Mittag-Leffler函数的一般形式可以总结为[18]

(18)

将式(18)代入式(16)中的第2式可得当σ>σp时的蠕变本构方程，即

σ>σp。

(19)

粒子群算法(PSO)[19]随机初始化每个粒子，每个粒子均表示一个可能性解，不断更新粒子速度和位置，通过迭代评估每个粒子并得到全局最优，基于MatLab编程实现粒子群算法，反演求解式(19)中最优模型参数。

4.2 模型拟合及参数求解

为了验证本文所建模型的辨识效果，借助许宏发[14]泥质板岩单轴压缩蠕变试验数据，由等时应力-应变曲线法[14]确定该岩石长期强度为11.50 MPa。通过本文所建模型进行拟合，采用文献[8]中未考虑时效损伤的分数阶蠕变模型进行对比，得到拟合值与试验值对比曲线(将加载应力标识在曲线上)，如图5所示。模型参数如表2所列。

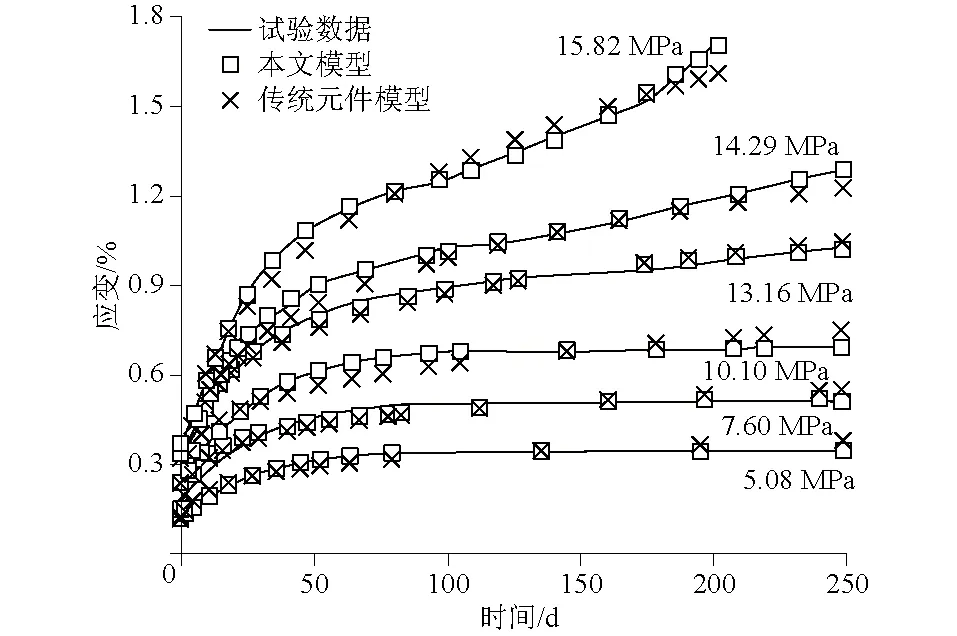
图5 不同加载应力下应变拟合值与试验值对比曲线Fig.5 Comparison between fitting values and test values of strain under varied loading stress

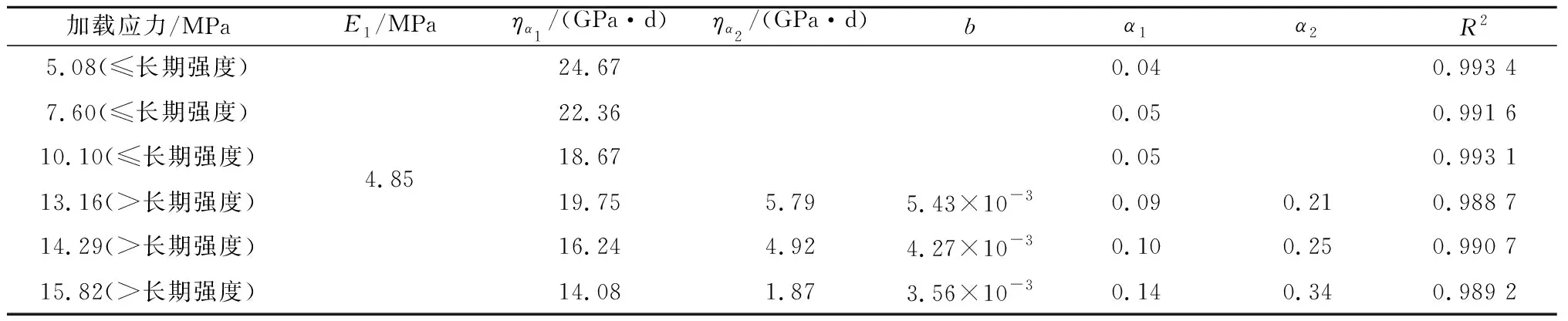
表2 模型参数Table 2 Model parameters

由图5和表2可看出，引用的未考虑时效损伤的分数阶蠕变模型的辨识能力尚可，平均R2为0.967 2，但对稳定蠕变阶段快结束部分以及衰减蠕变阶段的拟合存在较大偏差。本文所建模型拟合精度较高，平均R2达到了0.991 1，能较精准地识别岩石蠕变曲线，尤其是加速蠕变阶段。比较两者模型，本质上的不同在于本文所建模型有机结合了宏观的蠕变变形和微细观的损伤发展，不仅能较好地实现对蠕变量值的拟合，还可从“内外结合”的角度模拟岩石蠕变变形全过程。

4.3 岩石损伤发展

当应力超过长期强度时，岩石材料内部损伤才开始累积。泥质板岩蠕变试验中，在第4—第6级加载等级下，加载应力超过了长期强度，从第4级加载起，损伤开始累积，岩石内部微裂纹不断发育、延展，至第6级加速蠕变阶段末，微裂纹贯通，岩石出现宏观变形破坏。本文以第4级加载起，根据式(2)和表2中模型参数，绘制损伤累积曲线，如图6所示，利用玻尔兹曼[7-8]叠加处理第4—第6级蠕变曲线，得到分级加载形式，同时绘入图6中。

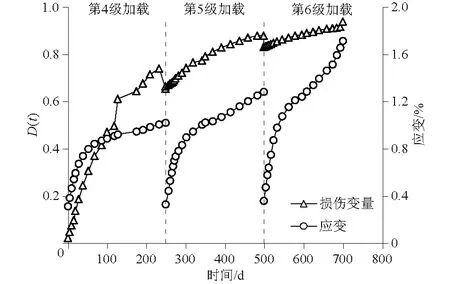
图6 损伤累积曲线Fig.6 Accumulated damage curves

由图6可知，损伤曲线随着时间增长而逐渐累积，至最后一级应力加载结束，损伤变量趋近于1。在第4、第5级以及第5、第6级应力加载之间，损伤变量出现了小幅的降低，分析其原因可能是应力提升的过程中，岩石内部微裂纹在外力增强作用下出现瞬间闭合现象，岩石应变此时随之小幅降低。待加载应力稳定后，岩石应变不断增长，损伤变量继续累积。

4.4 参数敏感度分析

加载应力的大小关系到损伤机制的触发，分数阶黏塑性体的阶数α2与岩石加速蠕变行为紧密关联，故分析加载应力和α2对蠕变发展的影响，判断其敏感度。以泥质板岩最后一级加载的模型参数为例，分别以加载应力和α2作为因变量，保持其它参数不变，绘制参数敏感度曲线，如图7所示。

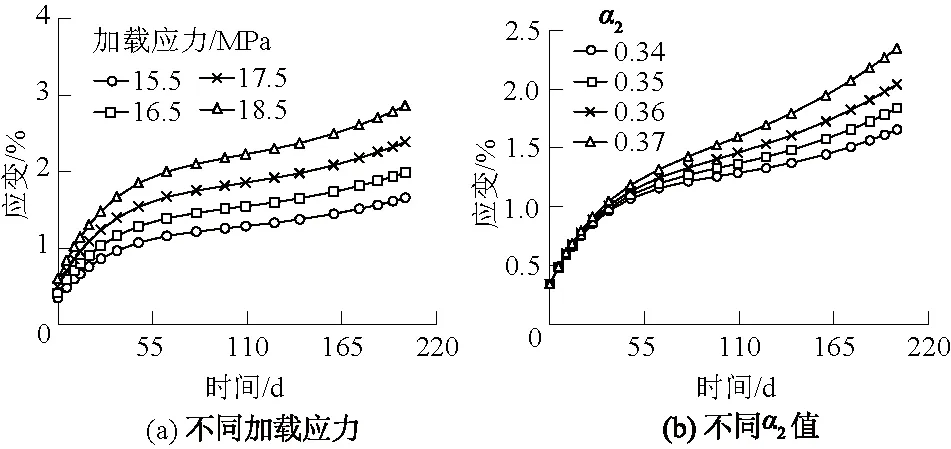
图7 参数敏感度曲线Fig.7 Curves of parameter sensitivity

分析图7(a)，岩石应变随着加载应力的提升而递增，加载应力影响整个蠕变过程的应变，对衰减蠕变阶段的曲线斜率有一定影响，但是不影响稳定、加速蠕变阶段的曲线斜率，由此可认为加载应力主要影响岩石衰减蠕变阶段速率和整体应变，故以最大应变作为敏感度判断依据。当加载应力从15.5 MPa提升到18.5 MPa时，最大应变从0.016 6增加到0.028 6，加载应力平均每1 MPa的增加引起了最大应变0.40%的变化。

分析图7(b)，岩石应变随着α2的增大而递增，α2影响稳定、加速蠕变阶段的应变和曲线斜率，几乎不影响衰减蠕变阶段的应变和曲线斜率，由此认为α2主要影响稳定、加速蠕变阶段的蠕变应变及速率，故以蠕变速率(从46.96 d—202.03 d取近直线段斜率)和最大应变和同时作为敏感度判断依据。当α2值从0.34增大到0.37时，最大应变从0.016 6增加到0.023 5，蠕变速率从3.78×10-5d-1增加到7.49×10-5d-1，α2平均每0.01量纲的增加引起了最大应变23.00%的变化，α2平均每0.01量纲的增加引起了蠕变速率123.67%的变化。

总体上，蠕变曲线随着加载应力和α2的改变而表现出一定规律性的变化，α2的敏感度高于加载应力。

4.5 模型适用性

为验证本文所建模型模拟不同岩石蠕变行为(尤其是加速蠕变阶段)的适用性，引用文献[20-21]中红砂岩和千枚岩单轴压缩各向异性蠕变特性试验研究得到的相关蠕变试验数据，分别通过本文所建模型和文献[8]引用模型进行拟合，得到拟合值与试验值对比曲线，如图8所示。

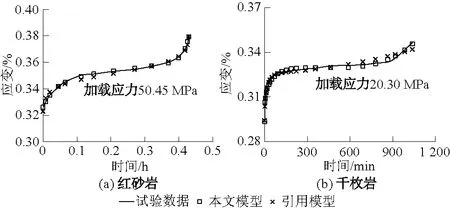
图8 不同岩石在不同加载应力下的应变拟合值与试验值对比曲线Fig.8 Comparison between fitting values and test values of strain under varied loading stress

由图8可看出，本文所建模型识别效果较好，拟合精度较高，R2分别为0.992 4和0.989 3。引用模型的R2分别为0.975 5和0.953 6，对于稳定、加速蠕变阶段的曲线识别存在较大偏差。

本文所建考虑时效损伤的岩石分数阶蠕变本构模型中弹性模量E1可通过试验确定，仅有ηα1、α1、ηα2、α2和b这5个参数需计算求解，模型结构简单、形式简练、参数较少、物理意义较明确，具有较强的蠕变曲线识别能力，对不同类型岩石蠕变行为的描述具有较好的适用性。

5 结 论

(1)本文引入连续损伤理论，基于弹性模量随时间衰减规律，根据能量损伤的方式以负指数型函数定义损伤变量，构建考虑时效损伤的弹性体，进行数据拟合验证该损伤演化方式的可行性。

(2)引入Riemann-Liouville型分数阶微积分算子理论，构建具有非线性特征的分数阶软体元件。利用该软体元件作为分数阶黏滞体描述岩石黏弹性应变，在该软体元件的基础上，结合损伤演化规律，建立考虑时效损伤的分数阶黏塑性体。

(3)联合分数阶黏滞体、考虑时效损伤的弹性体和分数阶黏塑性体，建立一个新的考虑时效损伤的分数阶蠕变本构模型。给出参数解析方法，利用泥质板岩蠕变数据验证模型合理性和优越性。损伤曲线随着时间增长而逐渐累积，参数α2的敏感度高于加载应力。通过红砂岩、千枚岩单轴压缩各向异性蠕变特性试验数据验证了模型的适用性。