◎郭俊娟 李国奎 （.昆明市第一中学西山学校，云南 昆明 65000；.昆明市西山区团结明朗中心学校，云南 昆明 650）

一、前 言

众所周知，当两个随机变量相互独立时，它们的相关系数为零（简称“不相关”）；反之，当它们不相关时，它们却未必独立.不相关且不独立的随机变量的例子已由诸多教科书与期刊文献所举出，兹不赘述.

一般来说，简单的例子容易理解和验证.因此，在构造“不相关且不独立”的例子时，一种倾向便是在取值较少（因而较简单）的离散型随机变量中去寻找.这里值得注意的有如下结论：

（1）服从一点分布（或者说以概率1 等于常数）的随机变量与任何随机变量相互独立.这种情况下，“不相关且不独立”是谈不上的.

（2）如果两个随机变量都服从两点分布，那么当它们不相关时，它们一定相互独立.此时“不相关且不独立”也是不可能的.

（3）存在两个随机变量，一个服从两点分布，另一个服从三点分布，它们不相关且不独立.

这就是说，要找出“不相关且不独立”的两个离散型随机变量的例子，对于随机变量取值个数的最低要求是其中一个能取两个值，而另一个能取三个值.为方便叙述，我们引入如下定义：

定义1.1设（X，Y）是一个二维离散型随机变量.如果X的边缘分布是两点分布，而Y的边缘分布是三点分布，那么称（X，Y）为（2，3）点随机变量.

本文在上述不相关且不独立的（2，3）点随机变量的例子基础上，分类讨论、详细研究（2，3）点随机变量相关性与独立性的各种情况.

二、预备知识和引理

（一）随机变量的不相关性

两个随机变量X与Y的相关系数规定为

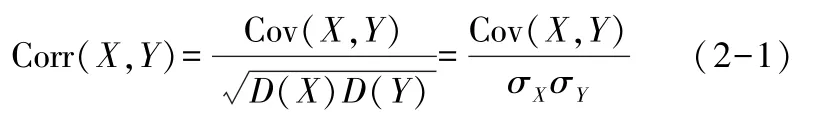
其中

（2－2）是X与Y的协方差，而D（X）＝Cov（X，X）为X的方差.

显然X，Y不相关的充要条件便是Cov（X，Y）＝0.［严格说来，如果D（X）与D（Y）之一为零，譬如D（X）＝0，那么Corr（X，Y）是没有定义的.但当D（X）＝0 时，X一定以概率1等于常数，这种情形我们是不予考虑的.］

此外，协方差还有如下性质：

（1）对称性：Cov（X，Y）＝Cov（Y，X）；

（2）双线性：Cov（aX1＋bX2，Y）＝aCov（X1，Y）＋bCov（X2，Y），a，b为常数；

（二）随机变量的独立性

我们只谈取值个数有限的离散型随机变量.那么，随机变量X与Y相互独立，其充分必要条件为对X的任意取值x和对Y的任意取值y，有

（2－3）式可以说成联合分布等于边缘分布的乘积.

为了给予独立性一种更直观的描述，设（X，Y）的联合分布列如表2－1所示，其中pi，j＝P（X＝xi，Y＝yj），qi＝P（X＝xi），rj＝P（Y＝yj）.我们称A＝（pi，j）为（X，Y）的联合概率矩阵.

表2－1 典型有限值域二维离散型随机变量联合分布列

引理2.1有限值域的离散型随机变量X与Y相互独立，其充要条件是它们的概率矩阵A中，任意两行（列）成比例，或者说A的秩为1.

如果X与Y相互独立，那么依（2－3）显然有

于是A的秩≤1.又由于A中所有元素之和为1，知A≠0，故A的秩恰为1.

反之，设A的秩为1，则由文献知

qi＝bi／b，rj＝cj／c

由此（2－4）式成立，而且

（三）条件分布

为了在某些场合避免提及联合分布，使叙述简明，我们使用条件分布的概念.在表2－1中，所谓当Y＝yj时X的条件概率分布是指这样一个列：其中

三、主要结果及例子

设（X，Y）是一个（2，3）点随机变量，则按定义1.1，它的分布列具有表3－1的形式.其中，由于X服从两点分布，为清晰起见我们不写x0，x1而改写作a，b；且p＝p0＋p1＋p2，q＝q0＋q1＋q2.这里，p，q，pi＋qi（i＝0，1，2）均不为零.

表3－1 一般（2，3）点随机变量的联合分布列

（一）主要结果

作为本文主要结果，我们将指出，X与Y的独立性和不相关性，首先取决于（X，Y）的概率矩阵中，有多少个列与X的边缘概率分布成比例，其次取决于yi（i＝0，1，2）的具体值.由于X的条件分布为

即当Y＝yi时，X的条件分布等于边缘分布.

对此我们有如下定理：

定理3.1设（X，Y）是一个（2，3）点随机变量，则

（ⅰ）如果Y至少有两个取值，使得X的条件分布等于边缘分布，则X与Y独立；

（ⅱ）如果Y恰有一个取值，使得X的条件分布等于边缘分布，则X与Y相关（因而必不独立）；

（ⅲ）如果Y取任何值时X的条件分布都不等于边缘分布，此时X与Y不独立，但可通过适当调整Y的值域（即表3－1中的｛y0，y1，y2｝）而使得X与Y不相关.

（ⅰ）不妨设当Y＝y1和Y＝y2时X的条件分布等于边缘分布，则有

因pi＋qi≠0，易见pi，qi均不为零.

这意味着（X，Y）的概率矩阵的两行是成比例的，因而由引理2.1 知X，Y独立.

（ⅱ）不妨设当Y＝y1时X的条件分布等于边缘分布，而当Y＝y0和Y＝y2时则不如此.则我们有

现转而考虑随机变量X′＝X－a，Y′＝Y－y0.

由于协方差的双线性，Cov（X′，Y′）＝Cov（X，Y）－Cov（a，Y）－Cov（X，y0）＋Cov（a，y0），

易见上式中涉及常数的一切项都为零，故Cov（X′，Y′）＝Cov（X，Y）.因此X′，Y′的相关性与X，Y的相关性等价.这样一来，（X′，Y′）的联合分布列如表3－2所示，其中

表3－2中，容易算得E（X′）＝b′q，E（Y′）＝y′1（p1＋q1）＋y′2（p2＋q2），E（X′Y′）＝b′y′1q1＋b′y′2q2.

表3－2 典型（2，3）点随机变量的联合分布列（简化假设）

注意到p＋q＝1，我们有

显然b′≠0（否则X′服从的就不是两点分布了），因此Cov（X′，Y′）＝0 等价于y′1（pq1－qp1）＋y′2（pq2－qp2）＝0 （3－4）.

将（3－2）代入（3－4），得到y′2＝0，但这又与Y′服从三点分布不符.因此，在这种情况下Cov（X′，Y′）＝0 不能成立，X′与Y′（X与Y）一定相关.

（ⅲ）此时pqi－qpi（i＝0，1，2）均不为零.另一方面，假定X，Y独立，则依独立性准则（2－3）式应有

移项得pq1－qp1＝0，与题设矛盾，故X，Y不独立.

为考察相关性，我们仍考虑随机变量X′＝X－a和Y′＝Y－y0.易见，只要取y′1＝k（qp2－pq2），y′2＝k（pq1－qp1）（3－5）.

其中，k为任意非零常数就能使得（3－4）式成立.依题设，y′1和y′2均不为零，且y′1－y′2＝k（pq0－qp0）≠0.

因此，0，y′1，y′2是三个互不相同的值，且当Y′取这些值时，在表3－2中有Cov（X′，Y′）＝0.于是，在（3－5）式的基础上，任取y0并通过（3－3）式来规定y1，y2，则y0，y1，y2是三个互不相同的值，且当Y取这些值时，在表3－1中有Cov（X，Y）＝0，即X，Y不相关.

（二）一些例子

我们通过具体例子来对定理3.1 加以说明，见表3－3、表3－4与表3－5.这里，由于定理3.1 的结论与Y的边缘分布以及X的具体取值无关，我们略去了Y的边缘分布一行，并设X的两个值为0 和1.

表3－3 情形（ⅰ）：X，Y 独立

表3－4 情形（ⅱ）：X，Y 相关，且相关性不能消除

表3－5 情形（ⅲ）：X，Y 不独立，但适当规定yi 的值可使其不相关

在表3－3中，概率矩阵的三个列显然成比例，故X，Y独立.独立与否是概率矩阵本身蕴含的性质，与X，Y的具体取值无关.

因此若要X，Y不相关，除非y2＝y0，而这是不可能的.

在表3－5中，概率矩阵的所有列都不与X的边缘分布成比例.这时X，Y不独立，但

因此只要取y1＝1，y2＝－1，y0＝0，就能使得Cov（X，Y）＝0，即X，Y不相关.

四、结 语

在绝大多数情况下，随机变量的独立性是比不相关性强得多的条件.实际上，设（X，Y）是一个二维离散型随机变量，X能取n个值而Y能取m个值，则X与Y的独立性意味着（n－1）（m－1）个方程［因为这时（X，Y）的概率矩阵中，其余（n－1）个行必须与某特定行成比例，而为了两行成比例又需要（m－ 1）个方程］，而X与Y的不相关性，即Cov（X，Y）＝0，仅仅是一个方程而已.只有在n＝m＝2 的情形下，不相关性才能与独立性等价.

本文所讨论的是n＝2，m＝3 的情形.在定理3.1 为这种情形划分的三种子情形中，（ⅰ）和（ⅱ）都与n＝m＝2 的情形紧密关联.事实上，对于（ⅰ）无须多言；对于（ⅱ），如果Y＝yi时X的条件分布等于边缘分布，那么条件随机变量为二值随机变量，这时我们便回到了n＝m＝2 的情形：X与不独立，它们必定相关，而由于

Cov（X，Y）＝Cov（X，）·P（Y≠yi），

X与Y也必定相关.于是，只有子情形（ⅲ）才是新的，它构成寻找“不相关且不独立”的（2，3）点随机变量的理论基础.

当然，我们还可进一步考虑n＝2，m＝k（k＞3）的情形，但从这里的讨论可以预见，这些情形与n＝2，m＝3 的情形并无本质区别，只是细节上更复杂而已.