Shumai Zhang(张舒迈), Liang Jin(金亮), and Zhi Song(宋智)

School of Physics,Nankai University,Tianjin 300071,China

Keywords: topological phase,PT symmetry,Wilson loop

1. Introduction

In recent years, parity-time (PT) symmetry has attracted increasing attention in non-Hermitian quantum mechanics.[1-11]PT-symmetric non-Hermitian systems,which may possess entirely real spectra,[12]have been widely explored in the optical waveguides,resonators,and cold atoms in optical lattices. The exceptional point (EP), known as thePT-symmetric phase transition point,indicates the transition between the exactPT-symmetric phase and the brokenPTsymmetric phase.[13-15]The EP means not only a bifurcation point of the energy bands,but also the eigenstate coalescence at the defective Hamiltonian.[16-22]The EP has potential application in the sensing.[23]

The investigation of topology has been extended to non-Hermitian physics.[24-47]Topological systems are of great significance in the condensed-matter physics.[48-66]The researches on non-Hermitian Su-Schrieffer-Heeger (SSH)chain, Chern insulator, and nodal-line semimetals have received great interests.[67-75]As the progress on optical realization of the topological systems, the field of topological photonics has been stimulated.[76]Edge states,[77,78]band theory,[79,80]and topological invariants[81-87]are major focuses in topological physics. The topological invariant, obtained from the Bloch bulk, characterizes the feature of energy bands.[83]The existence of edge states under the open boundary condition (OBC) is predictable by topological invariants under the periodic boundary condition(PBC),which is referred to as the bulk-boundary correspondence. The bulk-boundary correspondence is invalid in the non-Hermitian systems[88]when the non-Hermitian Aharonov-Bohm effect present,[89]and different approaches to find the topological invariant are developed.[89-91]

In this paper,we investigate the topological properties of aPT-symmetric non-Hermitian rhombic lattice. The non-Hermitian rhombic lattice is trimerized and has a quarter of a magnetic flux quantum enclosed in each triangular plaquette,where the balanced gain and loss present. Although the lattice hasPTsymmetry, the topological features are not inherited from the Hermitian rhombic lattice and the non-Hermiticity alters the band topology. The bulk-boundary correspondence of the non-Hermitian rhombic lattice is valid and the Bloch bulk captures the band topology. The topology is characterized by the global Zak phase,which predicts the presence of the topological edge states decaying from the lattice boundaries. The rhombic lattice supports a spectrum fully consisting of dispersiveless flat bands at the proper condition. Consequently, we find the anomalous edge states that compactly localize in two diamond plaquettes at the boundaries under the destructive interference.

The remainder of the paper is organized as follows. In Section 2, thePT-symmetric non-Hermitian rhombic lattice model and the energy bands are presented. In Section 3, the topological edge states and anomalous edge states in the non-Hermitian rhombic lattice are investigated. In Section 4, the global Zak phase is introduced and predicts the nontrivial band topology. In Section 5,the conclusion is summarized and the prospect is discussed.

2. Energy bands of the non-Hermitian rhombic lattice

Rhombic lattice The non-Hermitian rhombic lattice is depicted in Fig. 1(a), it is translationally invariant in the horizontal direction and is a trimerized lattice with three sublattices{A,B,C}. SublatticeAis passive, and sublatticesBandChave gain and loss with ratesγ. The gain and loss are staggered in the translational invariant direction. SublatticeAcouples to sublatticesBandCat the coupling strengthsg1andg2,and the Peierls phase factor eiΦpresents in the coupling with arrow, resulting in the synthetic magnetic flux 2Φenclosed in the diamond plaquette, whereΦ=π/2. The coupling between the sublatticesBandCisδ. The parameters are choseng1,g2,γandδ>0 without loss of generality. The unit cell of the non-Hermitian rhombic lattice is the two nearby triangular plaquettes containing six sites.

Bulk Bloch Hamiltonian We consider an equivalent Bloch Hamiltonian with simple structure to investigate the topological features of the non-Hermitian rhombic lattice,because of the complexity caused by multiple components working in the rhombic chain. The foundation of the equivalent lattice is the Bloch HamiltonianHkof the non-Hermitian rhombic lattice obtained by applying Fourier transformation to the real-space Hamiltonian,

whereG1=g1eiΦandG2=g2eiΦ.

Technologically, there are two consecutive steps to acquire the equivalent lattice. The first step is to obtain the 1D

Fig.1. (a)Schematic of the non-Hermitian rhombic lattice. The solid black(blue) lines represent reciprocal couplings g1 (g2). The black (blue) lines with arrows indicate nonreciprocal couplings,being g1eiΦ (g2eiΦ)for photons tunneling along the arrow and g1e-iΦ (g2e-iΦ) for photons tunneling against the arrow with Φ=π/2. The vertical coupling δ between sublattices B and C is in magenta. The sites in blue are passive and sites in green(red)have gain (loss). (b) Schematic of the non-Hermitian chain with nonreciprocal couplings δ±γ. (c)Schematic of the equivalent trimerized chain with reciprocal coupling µν. The unit cell is enclosed by the black solid box.

The lattice with reciprocal couplings is schematically depicted in Fig.1(c)in real space,where the repeat unit contains three sites. Therefore, the Bloch Hamiltonian of the equivalent chain depicted in Fig.1(c)is reduced to

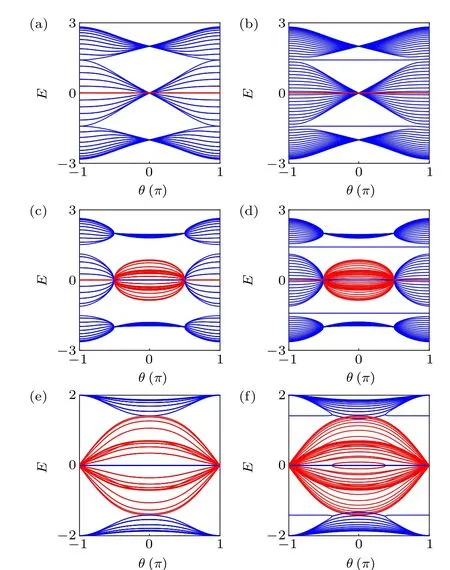
Fig. 2. Energy bands of the real-space rhombic lattice at different non-Hermiticity γ under PBC (left panels) and OBC (right panels). The real(imaginary) part of the band energy is in blue (red). The lattice model has 10 unit cells, being 60 sites in total. The parameters are g1 =g2 =1,δ =1-(1/2)cosθ with(a),(b)γ =1/2;(c),(d)γ =1;(e),(f)γ =3/2.

3. Edge states

This is a consequence of the destructive interference at the appropriate match of couplings,gain and loss,and the synthetic magnetic flux enclosed in the plaquette. The corresponding edge state still appears at the EP of the rhombic lattice, but the edge state is anomalous, only localized in two diamond plaquettes at the boundary.

Fig.3. Energy bands and edge-state amplitudes of the non-Hermitian rhombic lattice under OBC. (a) Energy bands at parameters g1 = γ = 1, δ =sinθ and g2 =1+(1/2)cosθ. All bands are entirely real with θ ranging from -π to π. The non-Hermitian model includes 10 unit cells with 60 sites. The horizontal axis indicates the site number. The amplitudes of edge states localized at the boundaries are numerically depicted at(b)θ =-0.6π,(c)θ =0.3π,and(d)θ =-0.1π.

Fig.4. Phase diagram of the non-Hermitian rhombic lattice in the g2-δ (g2-γ)plane. The parameters are g1=γ =1(g1=δ =1). Phase diagram in the g2-δ plane is the same as that in the g2-γ plane. The yellow (blue) region has a pair of left(right)edge states with energy The red area has two pairs of edge states with energies The white region has no edge states.

Fig.5.(a)The anomalous edge state with energy 0 localized at the left boundary of the non-Hermitian rhombic lattice. (b)The anomalous edge state with energy ± localized at the right boundary of the non-Hermitian rhombic lattice.

4. Topological characterization

The geometric phase reflects the topological property of the non-Hermitian rhombic lattice from another aspect in contrast to the edge states. The Zak phase for the non-Hermitian system is analytically generalized along the closed loopL,The integration path 2Lindicates two times of circling in the parameter space,to ensure the wavefunctions of energy bands come back to their initial conditions.[20]The energy levels have pairwise interchange after one circle and are restored after two circles, which is numerically demonstrated in the left panel of Fig.6. In the following, we introduce the numerical implementation of the Zak phase in the bulk. We divide the two loops intoNsmall segments and consider a 6×6 matrixAkifor a segment fromkitoki+1,T

he eigenvalues of the 6×6 matrixAare denoted asan,where the subscriptsn=1,2,3,4,5 and 6 represent different energy bands.

For each energy band, the accumulated Zak phase obtained via the Wilson loop approach is

The Zak phase associated with each energy band of the non-Hermitian rhombic lattice is not an integer overπin general case; however, the summation of the Zak phase for all the bands,which is referred to as the global Zak phase,is an integer overπand considered as a topological invariant. We give the expression of global Zak phase for the system

Notably,Γn/=Γ′nfrom their definitions;however,the summation of all eigenvalues of a matrix equals to the trace of the matrix, that is, the global Zak phaseΓ=Γ′can also be obtained via the Wilson loop approach.

The global Zak phase of the non-Hermitian rhombic lattice in both topological trivial and topological nontrivial phases are exemplified by the solid black lines in the right panel of Fig. 6, which presents the whole process of global Zak phase accumulation along the path integral in the parameter space. Topological edge states present in the region with nonzero global Zak phase 8π,and the 8πZak phase indicates topological edge states presenting in both two band gaps. In contrast,topological edge states are absent and the global Zak phase is 0. The numerical simulation of the Wilson loop approach is depicted by the red dashed lines in the right panel of Fig. 6, which are exactly in accord with the solid black lines. By employing the Wilson loop approach,the global Zak phase accumulated along two closed circles is 8πin the nontrivial phase, while the global Zak phase accumulated along two closed circles is 0 in the trivial phase.

Fig.6. Energy bands in momentum space(left panel)and global Zak phase in trivial/nontrivial topological phases (right panel). Both the energy bands and the corresponding eigenfunctions come back to their initial values after two circles. Parameters are (a), (b) θ =-0.6π, (c), (d) θ =0.3π, (e), (f)θ =-0.1π,and(g),(h)θ =-0.9π with g1=γ =1,δ =3+(1/2)sinθ,g2 =1+(1/2)cosθ. In (b), (d), (f), and (h), solid black lines indicate numerical results of global Zak phase in Eq. (13); red dashed lines indicate numerical results in the Wilson loop approach in Eq.(11).

5. Conclusion

We have investigated the topological properties of aPT-symmetric non-Hermitian rhombic lattice. The bulkboundary correspondence of the lattice is valid and the topological properties are encoded in the bulk Bloch Hamiltonian.The topological edge states present in the two band gaps in the topologically nontrivial phase. In addition,the anomalous edge states localized in two diamond plaquettes are induced by the destructive interference when all energy bands are flat.The Wilson loop approach is employed to acquire the global Zak phase for the topological characterization of the trimerized model. The global Zak phase is nonzero in the nontrivial phase, and the global Zak phase vanishes in the trivial phase.Our findings uncover the topological properties of thePTsymmetric non-Hermitian rhombic lattice and provide a prototypical approach for obtaining the topological properties of the 1D multi-band non-Hermitian topological phases.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grants Nos.11975128 and 11874225).