Peize Ding(丁霈泽) and Wei Yi(易为)

1CAS Key Laboratory of Quantum Information,University of Science and Technology of China,Hefei 230026,China

2CAS Center For Excellence in Quantum Information and Quantum Physics,Hefei 230026,China

Keywords: non-Hermitian physics,parity-time symmetry,open system,Lindblad equation

1. Introduction

Non-Hermitian physics has stimulated significant interest in recent years,[1-4]where particular attention has been devoted to its unconventional dynamics, peculiar critical behavior, and exotic band topology. A major driving force behind the booming field is the experimental implementation or simulation of these intriguing phenomena, particularly in open dissipative quantum systems.[5-7]Therein, the system undergoes particle or energy loss to its environment,and a non-Hermitian effective Hamiltonian becomes relevant by imposing postselection.[5,6]So far, a wide spectrum of non-Hermitian phenomena,ranging from parity-time(PT)-symmetry breaking and non-Hermitian criticality,[8-10]to non-Hermitian skin effects and non-Bloch topology,[11-18]have been experimentally implemented and explored in quantum mechanical systems such as the single-photon interferometry network,[19-21]cold atoms,[22-26]nitrogenvacancy centers,[27,28]superconducting qubits,[29]and trapped ions.[30,31]While most of these experiments investigate the single-particle aspects of the non-Hermitian physics, the interplay of non-Hermiticity and interaction is a fast-growing frontier with many open questions and fresh challenges.[32-36]

One of the key issues here is the relevance of non-Hermitian many-body Hamiltonians to open dissipative quantum systems.[37,38]While the latter is naturally characterized by trace-preserving density-matrix dynamics, the former requires a biorthogonal construction to ensure othornormality and recover the bosonic/fermionic statistics.[39]Further, the postselection framework in a many-body setting requires an unchanged particle number,[38]thus exacting a stringent limit on the timescale within which the non-Hermitian description can be applied. By contrast, this is not an issue with a noninteracting system, as is the case with the recent observations of PT transition and exceptional-point encircling in cold atoms.[22,26]Therein, a non-interacting atomic gas undergoes particle loss to the environment through optical pumping -a single-particle process. The dynamics is driven by a non-Hermitian effective Hamiltonian derived from the Lindblad master equation by dropping the quantum jump termcρc†(herecis the atomic annihilation operator andρthe full density matrix of the non-interacting system). This is equivalent to focusing only on atoms that are not lost to the environment, in the spirit of postselection. Specifically, under the quantum-trajectory description,[6]since dynamics of individual atoms are decoupled,they constitute an ensemble of independent trajectories with no quantum jumps,all driven by the non-Hermitian effective Hamiltonian.Therefore,given a large number of atoms,the corresponding non-unitary dynamics can be probed by making measurements on the remaining atoms.Should interactions exist,however,dynamics of atoms in general would not decouple. Applying postselection would then amount to requiring the complete absence of quantum jumps for any single atom within the ensemble, which becomes exponentially unlikely with an increasing atom number.

Nevertheless,we demonstrate in this work that,key non-Hermitian physics can still be probed in the full density-matrix dynamics over fairly long time,provided the open many-body system be dominated by few-body correlations. Using a minimal model of either two or three interacting fermions in a one-dimensional lattice, we first show that, under the non-Hermitian effective Hamiltonian of the corresponding Lindblad master equation, two-body scattering states of the system feature state- and interaction-dependent PT transitions.We then evolve the three-fermion dissipative system using the quantum trajectory scheme, taking into account the quantum jump processes. Remarkably, the decay of two-body correlations in this three-fermion open system follows the imaginary components of the complex eigenenergies of the twobody non-Hermitian scattering states. This enables us to extract the global exceptional point of the underlying two-body non-Hermitian system in the three-atom dissipative dynamics,from which the impact of interaction on the exceptional point is identified. Our results suggest that, non-Hermitian manybody physic can in principle be probed in the context of an open dissipative many-body setting, at least when both are dominated by few-body correlations.

Our paper is organized as follows. In Section 2, we present the model configuration, the corresponding Lindblad master equation,and the non-Hermitian effective Hamiltonian.We solve the two-body eigen problem of the non-Hermitian Hamiltonian using exact diagonalization in Section 3, where we reveal the existence of PT transitions and exceptional points in the scattering states. In Section 4, we solve the Lindblad master equation for a three-fermion system using the quantum trajectory approach,and show the relevance between the two-body correlations therein and the complex eigenenergies of the non-Hermitian scattering states. We summarize in Section 5.

2. Dissipative many-body system and non-Hermitian Hamiltonian

As illustrated in Fig.1,we consider fermionic atoms with two hyperfine states in a one-dimensional optical lattice potential. The corrsponding Hamiltonian is given by

Fig.1. Schematics of the dissipative lattice gas driven by the master Eq.(2).The single-particle loss(with rate Γ)is induced by optical pumping,via an electronically excited state,to a third state(not drawn)that is not trapped by the lattice potential. The r.f. coupling rate J and hopping rate t are defined in the main text.

We further consider the case where one of the hyperfine spin states (|↓〉) is subject to optical pumping, via an electronically excited state,out of the lattice potential. Under the Markovian approximation,the dynamics of the system is captured by the Lindblad master equation

While the full dynamics of the open system is governed by Eq. (2), under the quantum trajectory framework, the dynamics is understood as a non-unitary time evolution driven byHeff,which is further interrupted by quantum jumps{ck,↓}with relative probabilities{Γ δt|ck,↓|ψ(t)〉|2}. Hereδtis the coarse-grained time step,and|ψ(t)〉is the instantaneous state of the system.It is often argued that,when the effects of quantum jumps are negligible,the open system would evolve under the non-Hermitian HamiltonianHeff. Such a postselection argument plays a key role in connecting realistic open quantum systems to the rich and exotic non-Hermitian physics that has attracted much attention lately.[4]

For a non-interacting atomic gas withUs=Up=0, imposing postselection is conveniently equivalent to focusing only on the dynamics of atoms that are not lost to the environment. Since the full density matrix is just a direct product of single-particle density matrices, dynamics of each individual atom is driven by the same master equation. Further,as atoms that remain necessarily have not undergone the quantum jump process, the trajectories of remaining atoms are non-unitary evolutions driven by the same non-Hermitian effective Hamiltonian. This is indeed the case with the recent experimental demonstrations of PT symmetry and exceptional-point encircling in cold atoms.[22,26]

However, in an interacting system, the full density matrix can no longer be decomposed into single-particle ones.Postselection thus corresponds to a complete absence of quantum jumps,i.e.,it requires an unchanged total particle number.The non-Hermitian effective Hamiltonian is then applicable at short time, when the impact of the quantum jump terms are negligibly small.This is equivalent to the practice in Ref.[35],which projects the time evolution of the Lindblad equation onto the maximum-atom-number subspace. However,the corresponding time scale should become exponentially short with increasing particle number. Generally,consider anN-particle system undergoing single-particle loss with the rateΓ. The probability that not a single quantum jump occurs scales as～e-NΓ τ,whereτis the evolution time. Therefore,the probability of allNparticles still remain at the time 1/Γ(for an evolution starting att=0)is of the order e-N,and the time scale at which the non-Hermitian effective Hamiltonian dominates should bet<1/NΓ. Nevertheless, we show in the following that, two-body physics under the non-Hermitian effective Hamiltonian can be probed in the full density-matrix dynamics of the corresponding Lindblad equation,on time scales that exceed 1/Γ.

3. Non-Hermitian two-body scattering state

We first characterize the two-body problem under the non-Hermitian effective HamiltonianHeff. To connect with previous cold-atom experiments on PT symmetry,[22,26]we define the PT symmetric HamiltonianHPT=Heff+iΓ. While the addition of the pure imaginary energy shift iΓdoes not change key physics such as the emergence and location of exceptional points,it renders HamiltonianHPTPT symmetric in the non-interacting limit, with purely real (imaginary) eigenspectrum forJ>Γ/4(J<Γ/4).

In Fig.2, we show the numerically evaluated eigenspectra for two fermions along a lattice ofN=16 sites, with the parametersJ/t=0.04 andΓ/t=0.1. HereKcis the center of mass of the two-body state,which is a good quantum number of the system. In the non-interacting case [see Figs. 2(a)and 2(b)],HPTis in the PT-unbroken regime,with purely real eigenspectra. The PT symmetry is broken under a sufficiently large p-wave interaction, as the eigenspectra acquire imaginary components under a finiteUp[see Figs. 2(c) and 2(d)].This in contrast to the s-wave interaction,which does not affect the imaginary components of the eigenspectra [see Figs.2(e)and 2(f)]. Note that while discrete two-body bound states can be identified,for instance in Fig.2(e),it is the two-body scattering states within the continuum that acquire imaginary components. Importantly, we expect the PT transition point (or the exceptional points)of the non-interacting Hamiltonian be shifted by the p-wave interaction.

This is confirmed in Figs.3 and 4. Specifically,in Fig.3,we show the splitting of exceptional points in differentKcsectors under a finiteUp. With increasingJ,the scattering states sequentially coalesce in pairs at an array of second-order exceptional points. We identify the exceptional point with the largestJas the global PT transition point under the p-wave interaction,denoted byJc. The resulting PT phase diagram is shown in Fig.4. Apparently,the p-wave interactions shift the global exceptional point toward largerJ, consistent with the results in Fig.2.

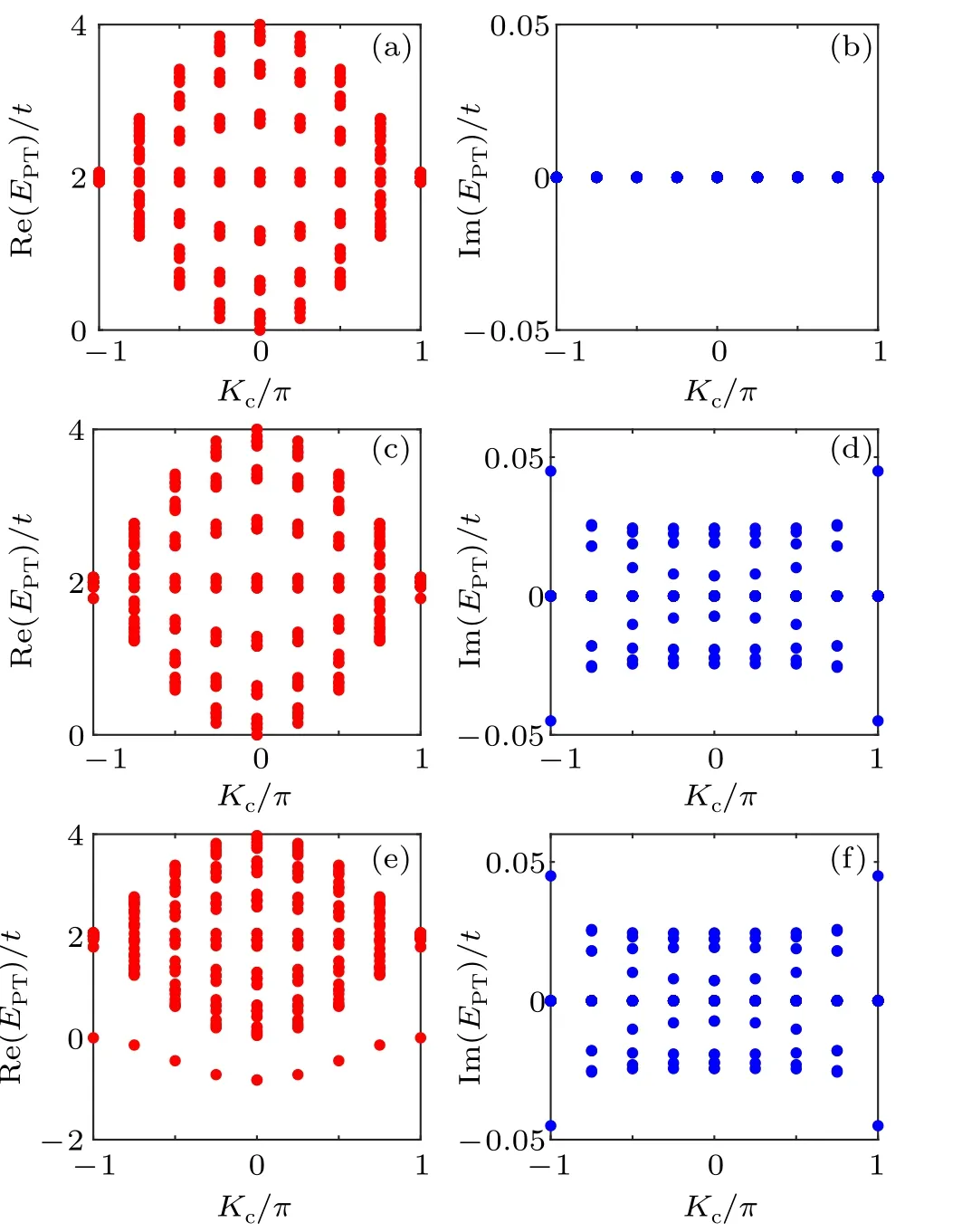
Fig. 2. Complex energy spectra of two fermions under the PT symmetric Hamiltonian HPT for (a) Us = 0, Up = 0, J/t = 0.04; (b) Us = 0,Up/t =-0.2, J/t =0.04; and (c) Us/t =-2, Up/t =-0.2, J/t =0.04.The left (right) panel shows the real (imaginary) components of the eigenspectra,with Kc the center-of-mass momentum of the two-body state.For all numerical calculates,we take a one-dimensional lattice with N=16 sites.

Fig. 3. Complex energy spectra of HPT as functions of J/t for (a) Kc =0 and (b) Kc =π. As J/t decreases, the scattering states coalesce in pairs at state-dependent exceptional points,through which their real components merge and imaginary components bifurcate. The full eigenspectra become completely real above a critical Jc/t,which is identified as the global exceptional point(or the global PT transition point).

Fig.4. PT phase diagram for HPT with Us =0 and Up <0. The global exceptional point Jc/t increases with larger p-wave interaction. The parameter used in Fig.3 is indicated by the vertical dashed line.

4. Probing non-Hermitian physics in open system

We now show that the global exceptional pointJcof the two-body scattering states in Fig. 4 can be probed from the density-matrix dynamics under the full Lindblad equation.Under interactions, information of the two-body exceptional point is difficult to extract from the particle-number dynamics of a many-body system. This is illustrated in Fig. 5, where we compare the particle-number evolution under the Lindblad master equation for systems initialized with different particle numbers,either with(Fig.5(a))or without(Fig.5(b))interactions. While the dynamics for different initial particle numbers appear to be the same without interactions,they generally differ under a finiteUp. This shows that non-Hermitian twobody physics cannot be directly probed using particle-number dynamics in a three-body dissipative system. Note that non-Hermitian two-body physics can be fully captured by a Lindblad equation initialized in the two-body sector,since quantum jump terms in a two-body sector only couple to three-body states.[35]

Fig.5. Comparison of total particle-number evolution under the Lindblad master equation for systems initialized with three atoms(blue solid), two atoms (red solid), and a single atom (yellow dashed), respectively,in the states|↑,k=-π〉⊗|↑,k=0〉⊗|↑,k=π-2π/N(N=8),| ↑,k = π〉⊗| ↑,k = 0〉, and | ↑,k = 0〉. The interaction parameters are(a) Up/t =-0.5, (b) Up =0, with Us =0, J/t =0.08, and γ/t =0.1 for both cases. To facilitate comparison, the particle numbers in all cases are normalized to one.

Instead, other observables should be adopted. For a minimal demonstration, we solve the Lindblad equation in a three-fermion system, initialized in the state|ψ(S)(Kc=-π)〉⊗|↑,k=π-2π/N〉. Here|↑,k〉is a single-particle state with hyperfine spin|↑〉and momentumk,|ψ(S)(Kc)〉is the two-body scattering state ofHeffwith a center-ofmass momentumKc, and|ψ(S)(Kc=π)〉is the eigenstate with the largest imaginary eigenenergy component,denoted as Im(E(S)). We take the system sizeN=8 for numerical calculations. Further,we define a normalized two-body correlation function

We evolve the Lindblad equation using the quantum trajectory approach, and plot the correlation functionG↑↑(k1=-π,k2=0)in Fig.6. Due to the particular choice of the initial state and the two-body correlation function, the decay of the correlation function follows the imaginary component of the two-body scattering state with the largest criticalJ. Thus,by fitting the exponents of decay inG,we are able to map out the global exceptional points in the phase diagram Fig.4,and retrieve key properties of a two-body non-Hermitian Hamiltonian from the full dynamics of an interacting three-body open system. We expect that this would hold true for many-body open systems, as long as the dominant correlations remain few-body in nature.

Finally,we note that,should we choose a different initial state and two-body correlation function, we would be able to extract information of other two-body scattering states.

Fig.6. (a)-(c)Time evolution of the normalized two-body correlation function G↑↑(k1 = -π,k2 = 0) (blue lines) under the quantum trajectory approach for (a) J/t = 0.04, (b) J/t = 0.08, and (c) J/t = 0.1. We take Up/t =-0.2, Us =0, and Γ/t =0.1 for numerical calculations. The red lines show the time evolution of the norm of the corresponding two-body eigenstate of the non-Hermitian Hamiltonian HPT. (d)Comparison between the imaginary component of the two-body eigenenergy under HPT(red line),with the numerically fitted exponent of the correlation-function decay(blue line and symbol). For the exponent,we numerically fit the time-dependent correlation function up to the time τt=5. For all our numerical calculations here, we take the lattice size N =8. We average over 2000 trajectories for the quantum-trajectory calculations.

5. Summary and discussion

Adopting a minimal model of a few dissipative fermions on a one-dimensional lattice, we show that PT transitions exist in the scattering states of the non-Hermitian Hamiltonian, and are shifted by the p-wave inter-atomic interactions.The interaction-shifted global exceptional point can be probed by measuring two-body correlations in the trace-preserving density-matrix dynamics driven by the Lindblad master equation. We therefore explicitly demonstrate a minimal scenario where key properties of a non-Hermitian interacting Hamiltonian can be probed in the context of an open system.

In particular,while one expects the non-Hermitian manybody Hamiltonian to be of relevance on a short time scale of 1/NΓ(see discussions in Section 2),it is remarkable that the two-body correlation captures key features of the two-body non-Hermitian scattering states at time scales even longer than 1/Γ(see Fig.6).We attribute such a phenomenon to the dominance of few-body correlations in the open dissipative system.Our result is complementary to previous attempts at connecting non-Hermitian many-body Hamiltonians with open dissipative systems,[37,38]and is relevant to cold atomic gases where few-body correlations dominate.

Acknowledgements

We thank Xiaoling Cui for helpful discussions. Project supported by the National Natural Science Foundation of China (Grant No. 11974331) and the National Key R&D Program of China (Grant Nos. 2016YFA0301700 and 2017YFA0304100).