Yue Li(李月) Zengqiang Chen(陈增强) Zenghui Wang(王增会) and Shijian Cang(仓诗建)

1College of Artificial Intelligence,Nankai University,Tianjin 300350,China

2Department of Electrical and Mining Engineering,University of South Africa,Florida 1710,South Africa

3Department of Product Design,Tianjin University of Science and Technology,Tianjin 300222,China

Keywords: multiple equilibria,curve axes,invariant tori,cluster-shaped conservative chaos

1. Introduction

It is accepted that chaos generated from smooth and non-smooth nonlinear dynamical systems described by ordinary differential equations(ODEs)or partial differential equations (PDEs) can be divided into two categories: dissipative chaos (chaotic attractor) and conservative chaos (also known as Hamiltonian chaos). Dissipative chaos widely exists in physical systems, such as Chua’s circuit,[1]double pendulum,[2]ballistic Dirac fermion systems,[3]the Peyrard-Bishop-Dauxois DNA model,[4]and some artificial nonlinear systems.[5-7]In contrast to dissipative chaos, conservative chaos can only be found in some theoretical models in the fields of celestial mechanics, molecular dynamics and hydrodynamics, such as the H´enon-Heiles system describing the motion of a star in a cylindrically symmetric and gravitationally smooth galactic potential,[8]two coupled anharmonic oscillators associated with molecular dynamics,[9]coupled Bloch oscillator equations representing electronic excitations of molecular dimers,[10]and hydrodynamic pilotwave system.[11]So far, the existing results have shown that the conservative chaos can be generated by Hamiltonian systems[12,13]as well as thermostatted systems.[14-17]Hamiltonian dynamical systems obeying Hamilton’s equations describe the evolutions of physical systems,[8-10,18]while the thermostatted dynamical systems are often used to describe the driven systems or the systems in contact with external fields, the systems connected to reservoirs or the mechanical pistons or particle reservoirs, as well as the constrained systems, and the systems away from equilibrium.[19]Recently,these studies related to thermostatted systems are focused on the investigation of their ergodicity and topology. Tapiaset al.proposed a logistic thermostat that is a variant of the Nos´e-Hoover oscillator and numerically studied the ergodicity of the system using four tests.[20]Then,Sprott discussed the ergodicity of several one-dimensional oscillators with a signum thermostat based on the logistic thermostat, including a signum thermostatted linear oscillator, a signum thermostatted nonlinear oscillator, a signum thermostatted Duffing oscillator,a signum thermostatted pendulum, and a signum thermostatted square-well oscillator.[21]As for the topological structure,Canget al.proposed an effective method to construct volumeconservative thermostatted systems by modifying the Hamiltonian energy function of a thermostatted system like the Sprott-A system.[22]Based on the method of Ref.[22],several interesting thermostatted systems with different topological structures were found.[23]

In chaos-based applications,pursuing higher-ranking security of cryptosystem needs the chaotic systems with more complicated topological structures. So far, multiple types of topological structure of dissipative chaotic flows have been well studied by many researchers in the field of nonlinear science, such as multi-scroll chaos,[24-26]multi-wing chaos,[27,28]multi-torus chaos,[29]and some new types of chaotic attractors with special topological structures.[30-33]Among these dissipative chaotic systems with complicated topological structure,coexisting attractors only depending on initial conditions are one of the hot research areas in the study of special chaotic systems. The coexisting dynamics have also been found in conservative systems, but the coexisting dynamics in Hamiltonian or thermostatted systems differ from the dissipative cases due to the energy/volume conservation of such systems. Although there is a common phenomenon that the invariant tori and conservative chaotic flows, as well as multiple periodic orbits coexist in conservative systems,little attention has been paid to the nonlinear dynamic characteristics of invariant tori and conservative chaotic flows.Similar to the multi-scroll and multi-wing chaotic attractor in dissipative systems, chaotic flows generated from conservative systems can manifest multiple clusters. The Sprott-A system,[34,35]a typical 3D thermostatted system,can produce volume-conservative chaotic flows with one single cluster for the given parameters and initial conditions.To find more complicated thermostatted system, Canget al.proposed a 3D thermostatted system with eight-cluster volume-conservative chaotic flows and separated invariant tori.[36]However, that work only presented numerical investigation and found some amazing dynamical behaviors. It is necessary to theoretically analyze the dynamic characteristics and find why the system can generate complicated conservative flows.In this paper,we mainly concentrate on the nonlinear dynamic analysis and numerical investigation of the system including the geometry of its Hamiltonian,curve axes,as well as multiple equilibria and their stabilities,and the mixture of chaotic seas and islands of invariant tori are numerically investigated for different initial conditions.

The rest of this paper is divided into seven sections as follows. In Section 2,we investigate the structure of the thermostatted system based on the formalism of the generalized Hamiltonian system. In Section 3, we perform the geometrical analysis of the Hamiltonian of the system including isosurfaces for different initial conditions and the local centers.In Section 4, the equilibria of the system and their stabilities are discussed based on two cases. The local curve axes of invariant tori and one eight-cluster conservative flow are explored in Section 5. Furthermore,in Section 6 we demonstrate the mixture of chaotic seas and islands of invariant tori of the thermostatted system. Finally,some conclusions are drawn in Section 7.

2. System model

The thermostatted system with eight-cluster conservative chaotic flows can be described by three first-order ordinary differential equations as follows:[36]

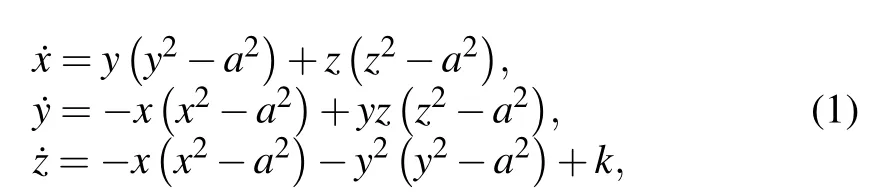
wherex,yandzdenote the state variables;a ∈R is the parameter; andk ≥0 represents the external excitation. Due to the existence ofk,the system(1)has no scalar function(Hamiltonian)satisfying the Hamilton equation,thus the system(1)is not a Hamiltonian system. However,the system(1)meets the description of the thermostatted system.[19]Whena=2 andk=1, the coexistence of separated invariant tori and eightcluster conservative chaotic flows appears in the thermostatted system for different initial conditions. At first glance,the system(1)is more complicated than the classic chaotic systems,such as the Lorenz system,[37]Chua’s circuit equation,[1]and Duffing oscillator,[38]because there are seven nonlinear termsyz,y2,x3,y3,z3,yz3andy4, and three linear termsx,yandz, and one constant termk. However, the system (1) can be converted into the following matrix differential equation:

and the external excitationu= (0,0,k)T. Numerical results have shown that there exist invariant tori and one eightcluster conservative chaotic flows.[36]It is well-known that improving the complication of topological structure of chaotic flows can improve the performance of chaos-based encryption algorithms. Recently, many scholars have focused on the studies of the conservative-chaos-based information encryption technologies and achieved promising results.[40,41]In Refs. [40,41], the topological structures of the conservative chaotic flows,which have been used by different information encryption technologies,are pretty simple. However,the system(1)can generate eight-cluster conservative chaotic flows,thus the system has greater potential for information encryption.

For such dynamical behaviors,the isosurface ofH(x)determines the whole topological structure, the number of clusters relies on the local centers ofH(X),the local curve axes of clusters are subject toJ(X)∇H(X),and the external excitationg(X)udestroys the motion of the system(1)on the isosurfaces ofH(X)and leads to the emergence of invariant tori and conservative chaos. The mechanism of the above characteristics will be investigated in following sections.

3. Geometry of H(X)

3.1. Isosurfaces

According to ∇H(X)=(f1(x),f2(y),f3(z))T, we have a Hamiltonian as follows:

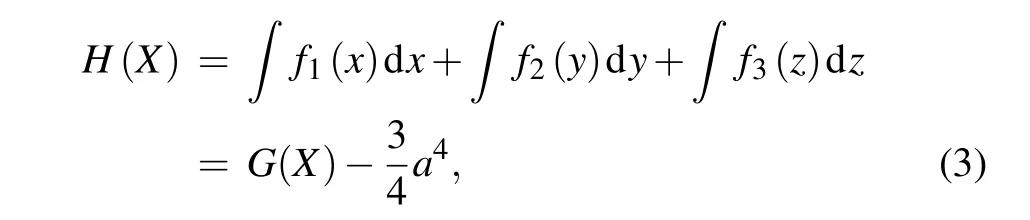
where

Obviously,G(X)≥0 denotes a closed surface that is compact and without boundary. Whenk=0,the Hamiltonian(3)is the first integral of the system(1). For differentG(X),the isosurfaces manifest various shapes, which can be summarized as the seven cases in Table 1.

Table 1. G(X)and its different shapes.

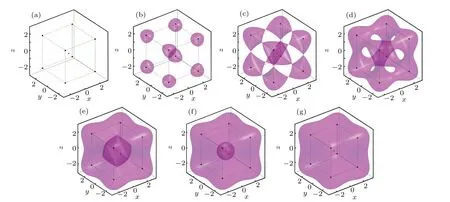
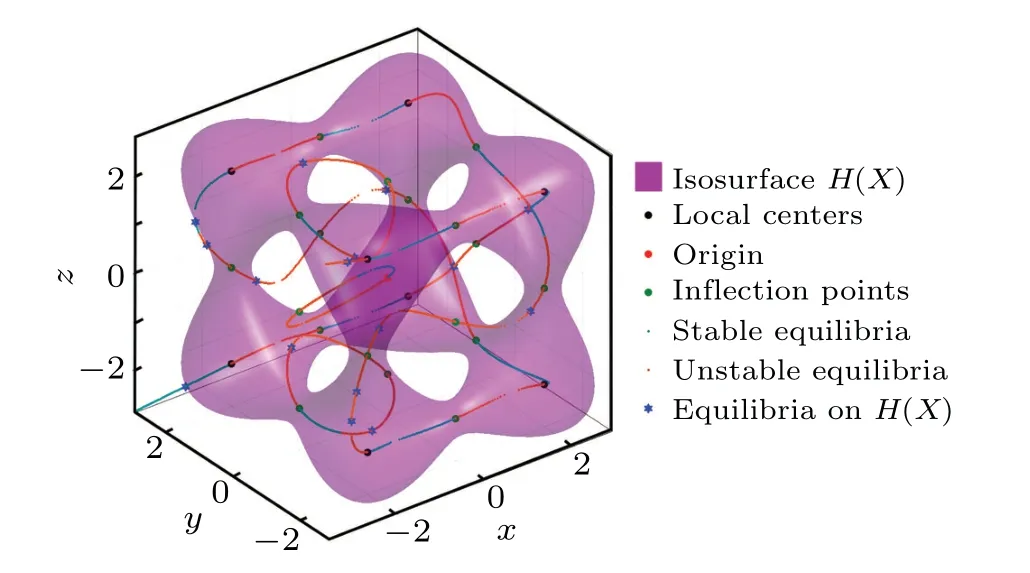
Fig.1. Cases of the 3D view of the isosurfaces(invariants)of H(X)with the increasing G(X0)for a=2: (a)eight separated points,(b)eight separated surfaces, (c) critical case between eight separated surfaces and one hollowed-out surface, (d) one hollowed-out surface, (e) critical case between one hollowed-out surface and one surface with one inner cavity,(f)one surface with one inner cavity,(g)one surface without inner cavity.

Whena=2, the isosurfaces of these seven cases can be exhibited in Fig.1. LetX0=(x0,y0,z0)Tbe the initial conditions of the system(1),then substitutingX0into Eq.(4)yields an isosurfaceG(X0). Withk=0, the trajectory starting fromX0,denoted byφ(X0,X,t),always runs onG(X0)because the conserved quantity of Eq. (2) does not vary over time, i.e.,dH(X)/dt=0.

3.2. Local centers of isosurfaces

Among these stationary points ofH(X), some points are the local minimum points and the others are the inflection points.Obviously,C1,2,···,8are just parts of Eq.(5),but ruling out other solutions of ∇H(X)=0 needs to use the Hessian matrix at each solution of ∇H(X)=0. The Hessian matrix ofH(X)is

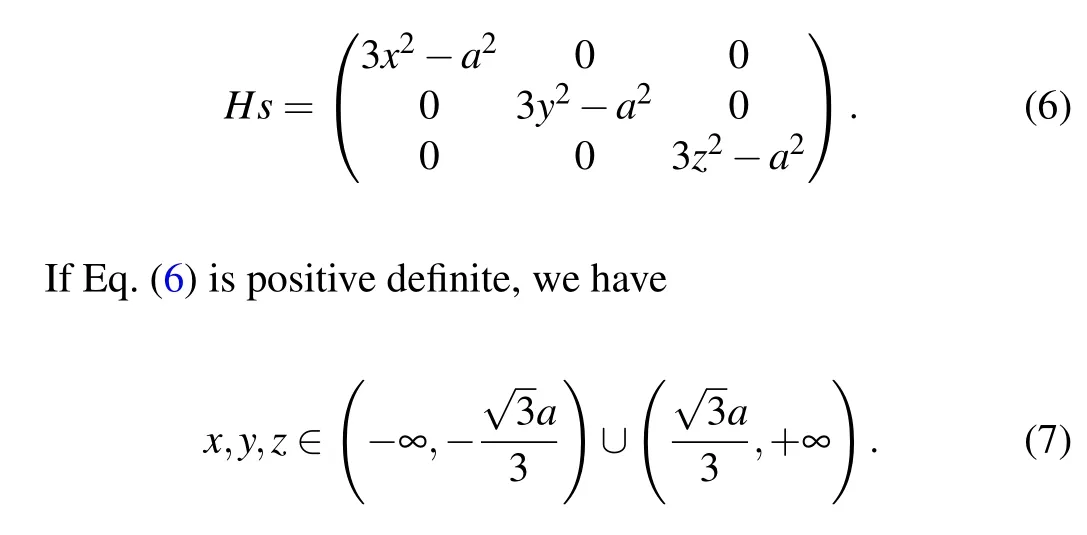
LetHs|Cn(n=0,1,...,26)be thenth solution of ∇H(X)=0,then substituting the solutionCn(n=0,1,...,26)into Eq.(6),we can find thatHs|Cn(n=1,2,...,8)is positive definite, which means thatC1,2,...,8are the local minimum points ofH(X).WhenG(X) gradually increases, the isosurface denoted byG(X) swells up fromC1,2,...,8, as shown in Fig. 1. Thus,C1,2,...,8are the local centers ofG(X),while the others are not,which agrees well with the results obtained by the method of completing the square.

For differentG(X0), the solutions of ∇H(X)=0 remain the same. WhenG(X0) equals 3.7959 and 4.4561, the solutions of ∇H(X) = 0 are shown in Figs. 2 and 3, respectively, in which the green dots denote the inflection points ofH(X), while the black ones represent the local centers ofH(X), which are exactly distributed in the eight corners of a single crystal lattice. Investigating the local centers ofH(X)is helpful for locating invariant tori and cluster-shaped conservative chaotic flows.

Fig. 2. For a = 2, the superposition of the isosurface H(X) with G(X0)=3.7969(purple surface),the local centers(black solid circles),the inflection points(green solid circles),the curves of stable equilibria(light blue curves) and unstable equilibria (orange curves) of the system(1)with k=0,and the equilibria on H(X)(blue hexagrams)in 3D phase space.

4. Equilibria and stability

For the nonzero parametera,the system(1)has countless equilibria fork=0 and no equilibrium fork/=0. Thus, the system (1) is a chameleon system.[42]For the case ofk=0,the equilibria of Eq. (1) can be obtained by ˙x=0, ˙y=0 and ˙z=0,and one obtains the equilibria set

As the solutions of ∇H(X) = 0 are also the solutions ofJ(X)∇H(X) = 0, the local centers and inflection points are in the curves of equilibriaEr. SubstitutingCn(n=0,1,...,26)into Eq.(9),the corresponding eigenvalues show thatC13,14,...,18andC23,24,...,26are saddle equilibria,while the others are nonhyperbolic equilibria. Whenr ∈[-3,3],the stability of all equilibria represented by Eq.(8)can be depicted by different color curves in Figs.2 and 3.The countless light blue points denote the stable equilibria,while the orange points represent the unstable equilibria. Note that the stabilities of all equilibria are not affected by the initial conditions.

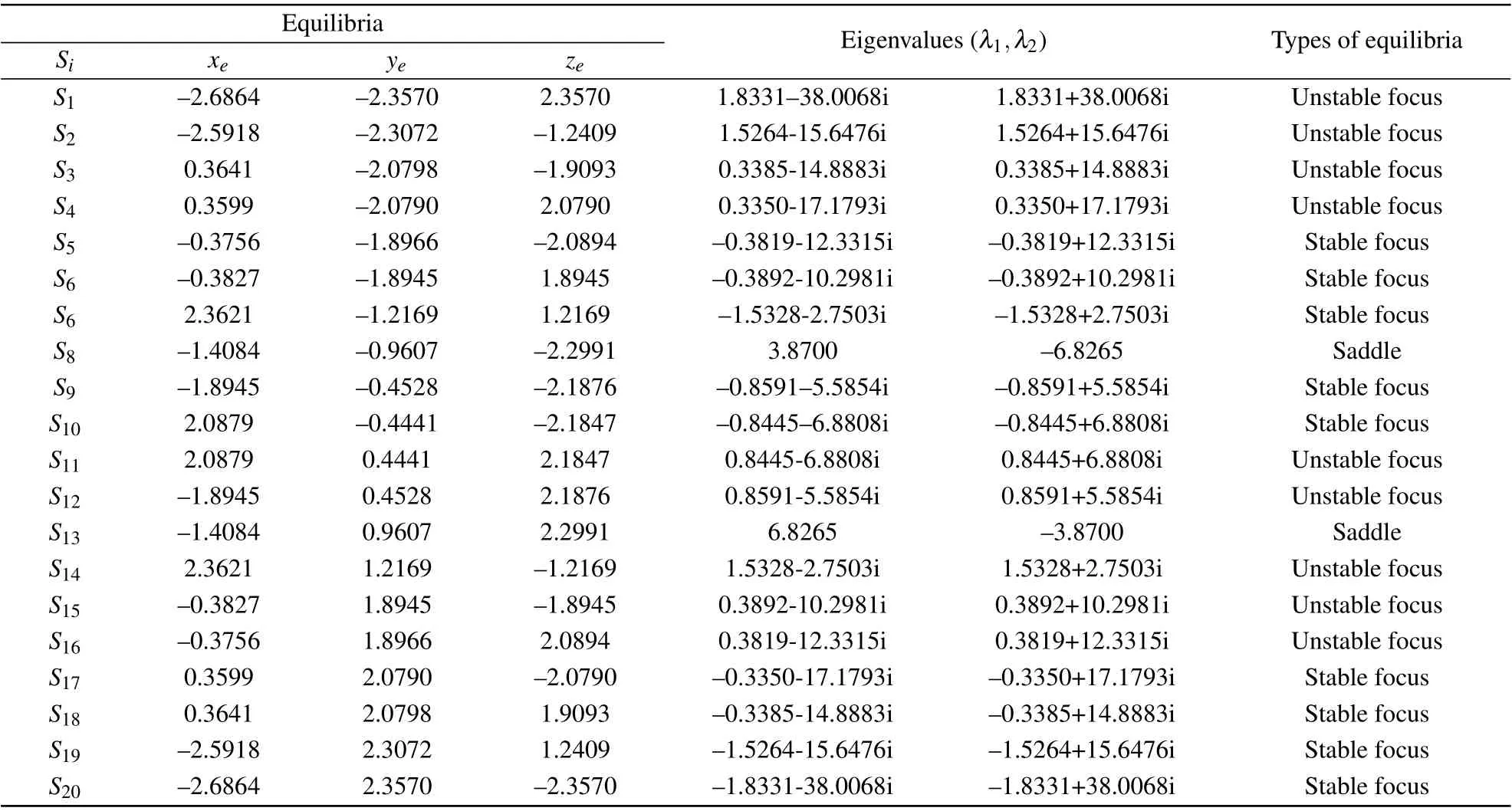
Table 2. Equilibria and their stabilities of the system(1)with k=0 on G(X0)=3.7969.

Table 3. Equilibria and their stabilities of the system(1)with k=0 on G(X0)=4.4561.

As mentioned above, for the given initial conditions,there are isosurfaces with different shapes whenk=0. According to the curves of equilibriaErin Figs. 2 and 3, we clearly see that there are some intersections ofG(X0)andEr.The numbers of the intersections depend onG(X0). WhenG(X0) = 3.7969, eight separated surfaces appear, however,whenG(X0)=4.4561, the geometry ofH(X) manifests one hollowed-out surface. For these two cases,their intersections ofG(X0)andErare listed in Tables 2 and 3,respectively.

From Table 2, we can see that there are twenty intersections ofG(X0) andEr, which means that the system (1) has twenty equilibria fork=0 on the isosurfaceG(X0)=3.7969.Among them,there are nine unstable foci,nine stable foci and two saddles. The trajectory starting from a point onG(X0)converges to one of the nine stable foci. However, whenG(X0)=4.4561,the eight separated surfaces inflate and merge into one hollowed-out surface,which leads to the change of the intersections ofG(X0)andEr.In this case,Table 3 records sixteen intersections ofG(X0) andEr, which include two stable foci, two unstable foci, and twelve saddles. All initial conditions onG(X0)result in the generated flows approaching one of the two stable foci. In Figs. 2 and 3, the blue hexagrams denote the equilibria for the givenG(X0).

Hereto,we have analyzed the geometry ofH(X)and the equilibria of the system (1) as well as their local stabilities whenk=0. In the following section, we focus on the global dynamical behaviors of the system(1)including invariant tori and conservative chaos whenk=1.

5. Curve axes of φ(X,X0,t)

As for cluster-shaped objects,there is always one or more invisible line or curve axis in it, such as a ball of wool and the field distribution in a dipole magnet. In the cluster-shaped conservative invariant tori and chaotic flows,there may be one or more invisible line or curve axes. For the system (1), we define the trajectory emanating from the initial conditionX0asφ(X,X0,t). Fork= 0,φ(X,X0,t) is always onG(X0),while fork/= 0,φ(X,X0,t) forms invariant tori and eightcluster conservative chaotic flows, which have been numerically explored.[39]

As mentioned in Section 3.1, there exists a first integralH(X)(Hamiltonian energy function)whenk=0. In this case,the system(1)is energy-conservative. However, whenk/=0,no Hamiltonian satisfies dH(X)/dt=0 because there exists energy exchange between Eq. (1) and external environment caused byk. To simplify system analysis, we can define the external system exchanging energy as

Obviously,the termkis the only route realizing the energy exchange between Eqs. (1) and (10). Fork=0,H′(X) is one first integral of Eq.(1),while fork/=0,H′(X)is one first integral of Eq.(11). Ifφ(X,X0,t)denotes the trajectory generated by Eq.(11),φ(X,X0,t)should run on the hypersurfaceH′(X0)in (x,y,z,v) space. Since the system (1) is the subsystem of the system (11),φ(X,X0,t) is the projection ofφ(X,X0,t) in(x,y,z)space.

Without the external excitationk,φ(X,X0,t) approaches one of the stable equilibria (intersections ofErandG(X)).However, when the external excitation is introduced into Eq.(1),H(X)andErwill be destroyed. Here,φ(X,X0,t)running onG(X) approaches or keeps away from the neighborhood ofEr. In a small enough area nearEr,we can reach the following approximate solution of Eq.(1):

where the superscriptsdenotes the stable equilibria inErwhenk=0.Eris not an isolated point but multiple curves of equilibria,andφ(X,X0,t)not only converges to or keeps away fromErbut also moves withEr. This dynamical behavior differs from that of the case of an isolated equilibrium. IfEris stable,φ(X,X0,t)converges toEr;conversely,φ(X,X0,t)is away fromEr. It should be noted thatkcan be regarded as the speed of the local movement nearEr.

For 3D thermostatted systems without external excitation,chaos does not appear due to the existence of the invariant.When the external periodic or fixed signal is introduced into the system,the conservative dynamics including conservative chaos and invariant tori may appear. Although the local dynamical behaviors can be determined by the Jacobian matrix of Eq. (1),the dynamical behaviors nearErcan be imaged even thoughk/=0. As long ask/=0,the local dynamical behaviors nearErcannot be sustained over time becausez(t)≈zse+kt.Fora=2,the system(1)undergoes invariant tori and volumeconservative chaos for differentX0.

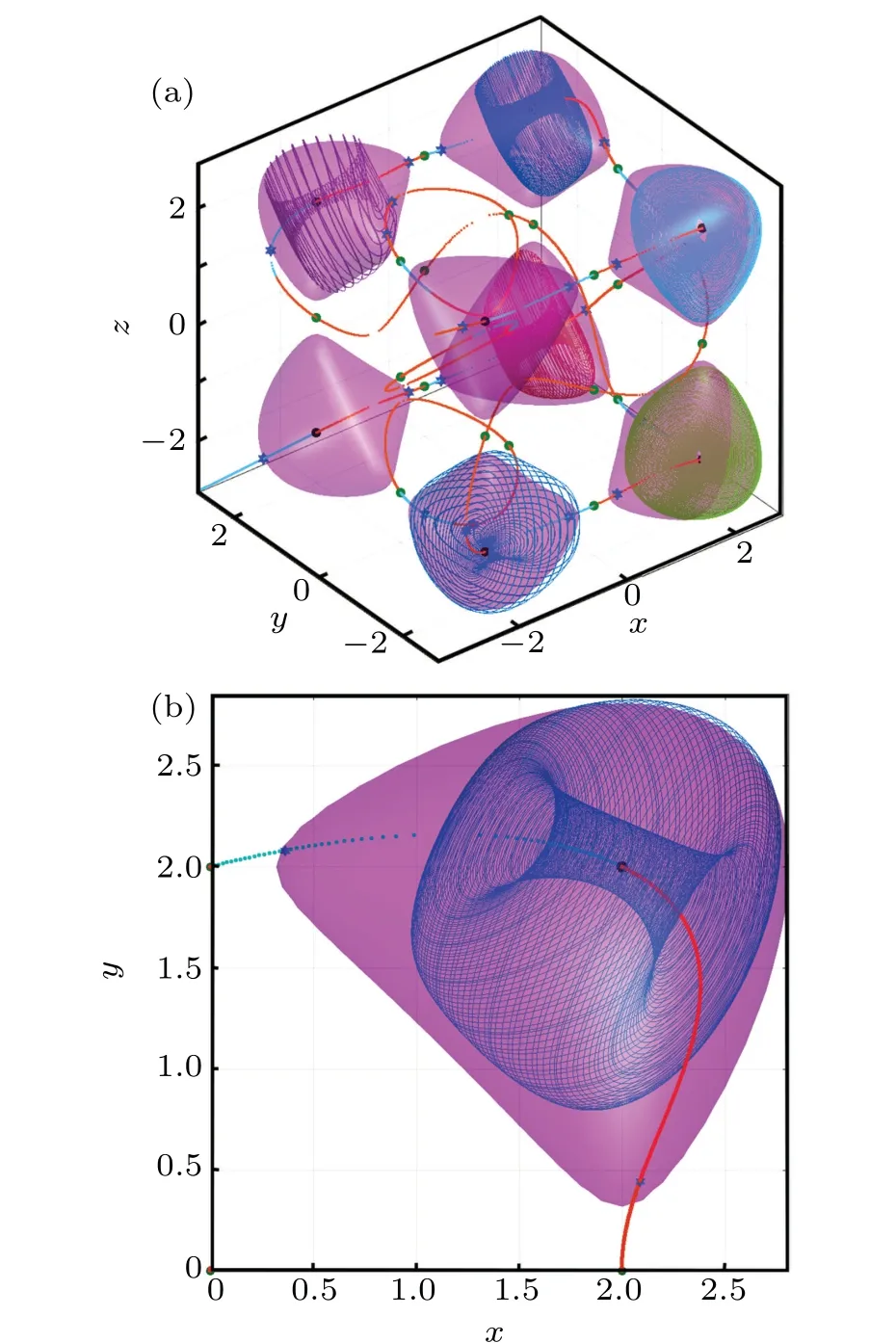
Fig.4. Invariant tori surrounding six isolated isosurfaces where different colors of tori denote the flows generated by the system (1) under different initial conditions with the corresponding curve axes: (a) 3D view of the six tori connected by two curve axes,(b)2D magnification of the tori generated by the system(1)(blue)with ,local center and curve axis.

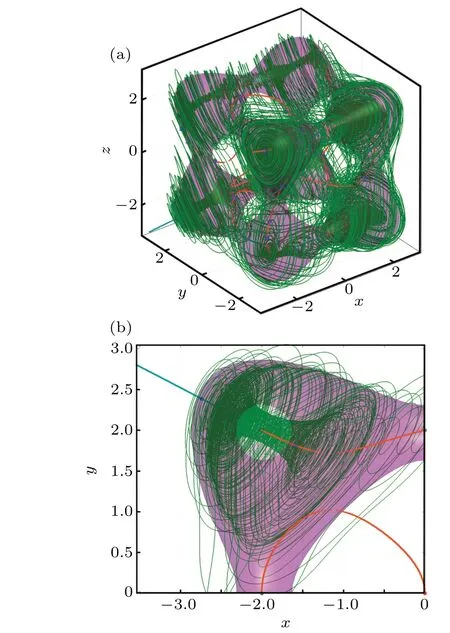
Fig. 5. Chaos surrounding the one hollowed-out surface where the green trajectories denote the volume-conservative chaotic flows generated from Eq. (2) with ) and the corresponding curve axes: (a) 3D view of the eight-cluster volume-conservative chaotic flows,(b)2D magnification of the chaotic flows of one of clusters,local center and curve axes.

Based on the numerical analysis of the two cases, the curve axes ofφ(X,X0,t)have three significant characteristics as follows:

(1) The curve axes consist in the curves of equilibriaErof the thermostatted system with zero external excitation.

(2)Any one of the curve axes must have a center locating in the curves of equilibriaEr.

(3) With the center as a boundary, the equilibria on one side of the curve axes are stable (curves colored light blue)and the equilibria on another side are unstable(curves colored orange),as shown in Figs.4(b)and 5(b).

According to Figs.2 and 3, there are eight curve axes inEr, and the system (1) may have eight invariant tori or one eight-cluster conservative chaotic flow under different initial conditions onG(X),which were verified by the numerical results in Figs.4 and 5.

6. Chaotic seas and stable islands

Dynamical systems can be understood from the motions of their state points on the Poincar´e sections. The Poincar´e return maps of Hamiltonian and thermostatted chaotic systems consist of chaotic seas and islands of invariant tori. Generally,there are chains of islands around each of the critical invariant tori,and chaotic seas remain in close contact with the critical invariant tori encircling countless hierarchical islands of invariant tori.[43]For the system (1) witha=2 andk=1, the Poincar´e return map on the surface of the sectionx=2.1 is plotted in Fig. 6, which shows a mixture of chaotic seas and islands of invariant tori. It can be found from Fig.6 that there are four groups of chains of islands of invariant tori, i.e., G1,G2,G3 and G4,and all of them contain five families of invariant tori. Moreover,we can see that the chaotic motion is stuck by the critical invariant tori and stays there for a long time since the local expansion rate of nearby stable invariant tori is approximately zero. The stickiness of chaotic motion to the islands of invariant tori occurs repeatedly and intermittently,and produces a long-time correlation of chaotic motion. Also,we can clearly observe that the return points on the Poincar´e section atx=2.1 form two white stripes, which means that there are no return points distributed in the stripes. The stripes rely on the curves of equilibriaEr. According to the equilibria set(8),eliminating the state variablexyields

which indicates that the curves of equilibriaErprojected on the (y,z) plane manifest one line through the origin, and one ellipse centered at the origin. If we plot the line and the ellipse on the Poincar´e section atx=2.1,we can find that the line and the ellipse are exactly filled in the two white stripes,as shown in Fig.7.

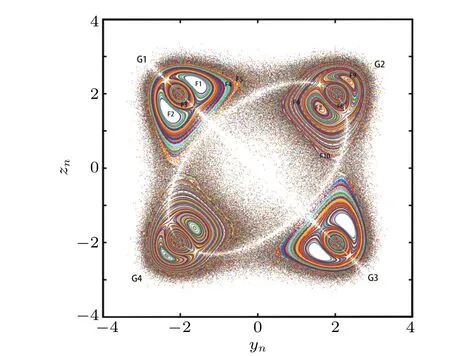
Fig.6. Poincar´e return map to the surface of the section x=2.1. The family of invariant tori F4(or F6)in G1(or G2)encircles F1,F2 and F3(or F7, F8 and F9), while F5 and F10 are isolated. Here, the Poincar´e section x=2.1 is chosen based on some simulations since this Poincar´e section is representative and can show more information related to stable islands.

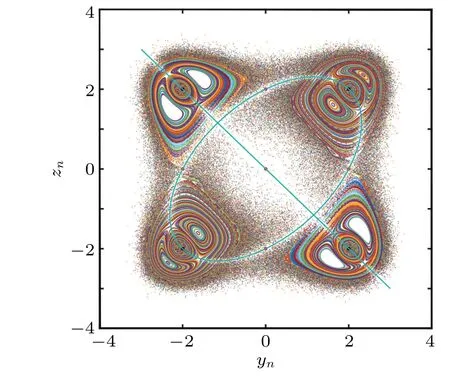
Fig.7.Superposition of the Poincar´e return map and the projected curve axes Er on the(yn,zn)plane at x=2.1.

7. Conclusion

In literature,there have been few studies on the dynamic characteristics analysis of conservative flows from thermostatted systems. Based on one complicated thermostatted system,we systematically investigate its multiple equilibria and curve axes of cluster-shaped invariant tori and one eight-cluster conservative chaotic flow. Moreover, several numerical techniques have been used to show that the geometry of the Hamiltonian including different shapes of isosurface and the local centers is explored for different initial conditions. Without external excitation,there exist curves of equilibria in the system in which some segments are stable and others are unstable,and the intersections of curves of equilibria and isosurface determine the dynamical behaviors on the isosurface. However,if there is an external excitation, the curves of equilibria of the system will disappear,and the disappeared curves of equilibria become the curve axes of the invariant tori and eightcluster conservative chaotic flows. Moreover,the three significant characteristics of curve axes are summarized based on the numerical results. Furthermore,we investigate the chaotic seas and islands of invariant tori for the thermostatted system with given parameters,which shows that the chaotic motion is strongly trapped in the vicinity of each critical invariant tori.

However, there is still one open research question. For given initial conditions(initial energy),there exists energy exchange between the thermostatted system and the external environment. When the energy exchange causes the system to move only near one of curve axes,an invariant torus appears.If the system moves and passes through more than one curve axis, multiple cluster-shaped conservative chaos will arise.Why do different initial conditions lead to different dynamics of the energy exchange process? Further studies are necessary to find a solution to this question.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 61973175 and 61873186),the South African National Research Foundation (Grant No.132797),the South African National Research Foundation Incentive (Grant No. 114911), and the South African Eskom Tertiary Education Support Programme.