Propagation dynamics of dipole breathing wave in lossy nonlocal nonlinear media
2022-01-23JianLiGuo郭建丽ZhenJunYang杨振军XingLiangLi李星亮andShuMinZhang张书敏
Jian-Li Guo(郭建丽), Zhen-Jun Yang(杨振军), Xing-Liang Li(李星亮), and Shu-Min Zhang(张书敏)
College of Physics,Hebei Key Laboratory of Photophysics Research and Application,Hebei Normal University,Shijiazhuang 050024,China
Keywords: breathing wave,propagation,variational method
1. Introduction
Nonlocal optical soliton and breather waves can propagate stably in highly nonlocal nonlinear mediums (HNNMs)when nonlinear self-focusing dynamically balances diffraction, therefore nonlocal nonlinear media have attracted extensive attention recently.[1]A nonlocal medium can exhibit a kind of nonlinear response that the refractive index change of the material at a specific location depends on the intensity of a specific neighborhood at that location.[2,3]In nonlinear media, one kind of the most studied materials are those with high nonlocality,which means that the characteristic length of the nonlinear response is much larger than the beam width,such as nematic liquid crystal mediums(NLCMs),[4,5]nonlinear ion gas,[6]thermal interface,[7]and lead glass.[8]It has a profound influence on the study of propagation dynamics of optical spatial solitons and breathing waves.
The concept of breathing wave plays an important role in explaining and simulating the evolution dynamics of light beams in HNNMs. The theory proposed by Snyder-Mitchell model promotes the intuitive recognition of self-localized wave packets in 1997.[2,9]Previously, the propagation dynamics of beams were well discussed through numerical simulation[10]or inverse scattering modeling and so on.[11]In recent years,people often use Jacobi elliptic function,[12]variable separation method,[13]variational method (VM),[14-16]and other integration algorithms to solve relevant problems.Moreover, some properties of beams in propagation process have been verified in many aspects, such as nonlocalization in dispersion shock wave,[17]Anderson localization,[18]gradient mutation, guide wave distribution coupling, and photon condensation.[19]
Due to foreseeable applications in optical communication, optical switch, and optical tweezers, research of beam propagation characteristics is appealing increasing interests.Studies have shown that nonlocal nonlinearity can support a variety of new soliton states, including bright soliton,[20]surface wave soliton, multimode soliton propagation, helical interaction,[21,22]and so on. The evolutionary characteristics of different types of breathers can be explored and applied. In 2004, Guoet al.obtained the evolution of the soliton in an HNNM,focused on the nonlocal nonlinear Schr¨odinger equation (NNLSE).[9]In 2006, the interaction of nonlocal solitons in NLCMs can be controlled by the degree of nonlocality, which has been proved experimentally by Huet al.[23]In 2011, Maet al.addressed the existence of multipole interface solitons in one-dimensional thermal nonlinear media and found that there exist two kinds of tripole and quadrupole interface solitons and three types of fifth-order interface solitons, respectively.[24]They obtained the analytical solutions of surface solitons and breathers in an HNNM, and obtained the critical power and the period of breathers by numerical simulation.[25]In 2016, Alberucciet al.discussed the deviation process of soliton and breather in real materials based on the Snyder-Mitchell model.[26]In 2019,Chenet al.predicted the fluctuation of breathers using the VM in an HNNM.[27]In 2020, Shenet al.studied dipole solitons and vortex solitons,and discussed the linear anisotropic diffraction in nonlinear media using VM and split-step Fourier transform.[28]The soliton modes and stability of optical pulses in nonlocal nonlinear fused double core planar wave guides have been explored by Gaoet al.,the Bessel-Gaussian beams modulated by airy mixture have been studied based on vector diffraction theory.[29,30]In our previous works, we discussed the interaction between anomalous vortex beams,[31]the evolution of higher-order hyperbolic sine Gaussian solitons and the propagation dynamics of dipole breathers in nonlocal nonlinear media.[32,33]We also theoretically discussed the propagation and interaction characteristics of various moving solitons and soliton arraies,including the breathing state in HNNMs.[34-38]
As a typical representative of HNNMs,NLCMs have received a great deal of attention experimentally and theoretically. For example, the self-trapping of light beams has been tested in NLCMs via the Lagrangian approach.[4]Considering the interaction between solitons and boundary conditions,behavior of accessible solitons with diffusion-like nonlinear response in nonlocal media is investigated.[10]In addition,nonlinear propagation of optical solitons through pure photothermal nonlinearity in a dye doped NLCM has been reported by Kwa´snyet al.[39]Using the nonlinear response of NLCMs,the molecular direction of optical breather formation and the stability of propagation dynamics are studied by Junget al.[40]The formation, decay and subsequent regeneration of a optical beam in a medium with cubic quintic self interaction and strong dissipative nonlinearity are reported and analyzed by Reynaet al.[41]However,the propagation of dipole breathing wave (DBW) in lossy HNNMs has rarely been explored. In this work,we aim to study the evolution dynamics of DBW in a lossy HNNM based on the VM.
The frame of this paper is as follows. In Section 2 we briefly outline the theory and mathematical method on which our investigation are based. In Section 3 the analytical and numerical results of the DBW in lossy highly nonlocal nonlinear systems is carried out. In Section 4 this paper is concluded.
2. Mathematical model




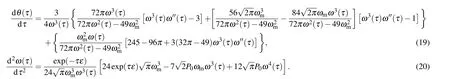

which is a constant based on Eq.(17).Pτ=∫+∞-∞|Ψ(ξ,τ)|2dξis the power during propagation, and it decreases exponentially along propagation distance.
In theory,a(τ),ω(τ),c(τ), andθ(τ) will be acquired because of Eqs.(17)-(20), and the analytical propagation expression of the DBW will be got. In the following section,the propagation expression is solved and the propagation dynamics of the DBW are discussed in detailed. More importantly,the conclusions in this work are apply to else shapes of breathers and can be popularized to other nonlocal optic solitons.
3. Results and discussion
In this section,the effects of the losses on the beam width,light intensity,wavefront curvature,and propagation state will be detailed discussed analytically and numerically.
In Eqs. (17)-(20) we make Eqs. (18) and (20) as zero,i.e., dω/dτ=d2ω/dτ2=0,the process is the case of no loss of medium. The beam width of the DBW is a constant during propagation, and it is a soliton state. We define the input power as critical power,and it is expressed as

Here we are dealing with the propagation of a beam in the HNNM, the response degreeωmof the medium is large, the critical power is relatively accurate.
In the following we discuss the case of loss of the medium,therefore dω/dτ/=0,the width of the DBW varies during propagation. In Newton’s second law,Eq.(20)is used to expresses the motion of a particle with equivalent mass 1.

With the emergence of nonlinear optics, there are many connections between wave optics and classical mechanics.For example, the ideas and methods of Lagrange function and Hamiltonian can be used to analyze the optical properties of nonlinear media. In most cases, the experimental results of the mechanical model are consistent with the actual numerical integration results. We give the variation of DBW beam width which is similar to that of classical mechanics, as shown in Fig.1.
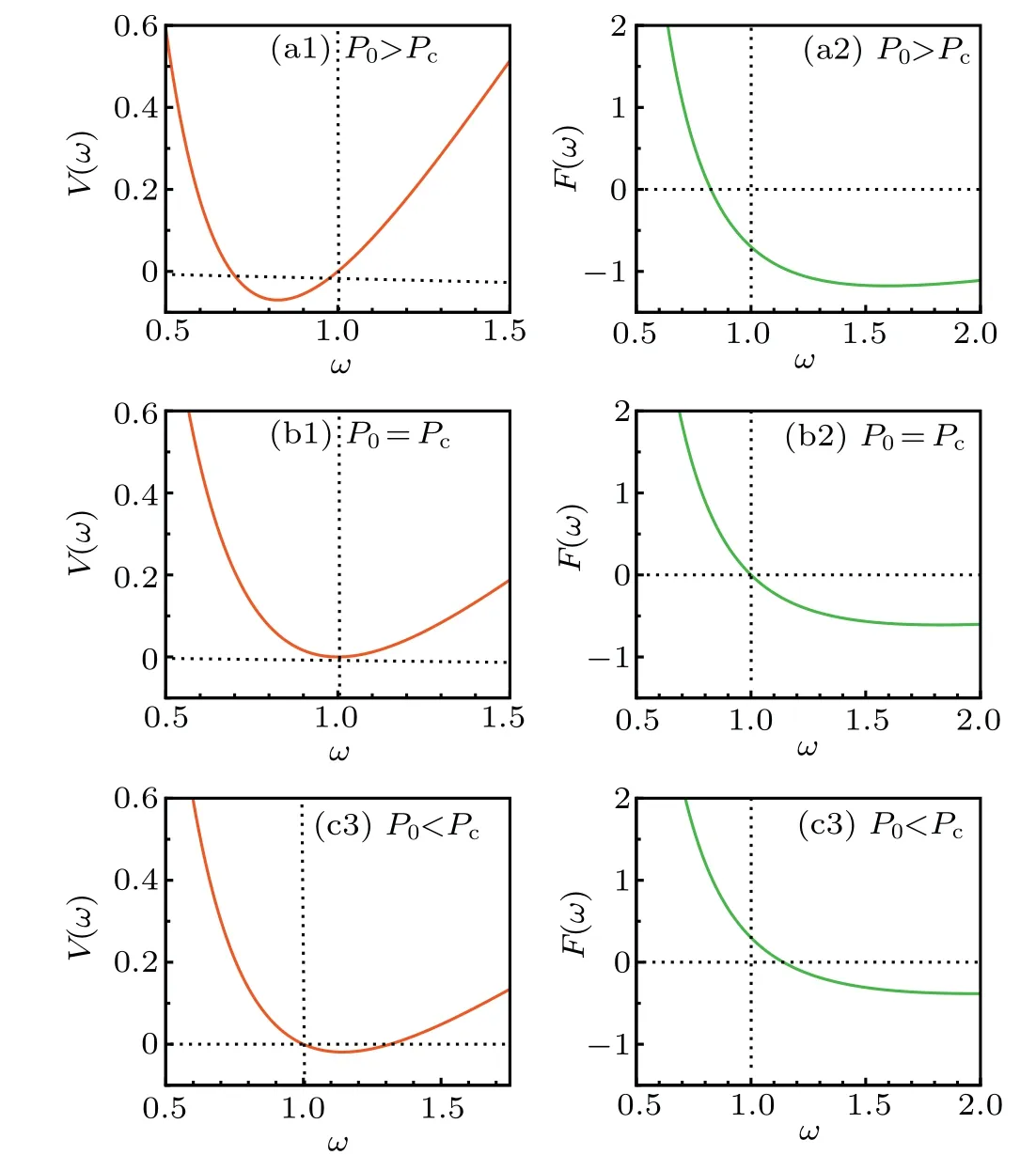
Fig.1. The equivalent potential energy(column 1)and equivalent force(column 2) varies with beam width under different incident powers.P0=0.92Pc for(a1)and(b1),P0=1.0Pc for(a2)and(b2),P0=1.08Pc for(a3)and(b3). Other parameters are ωm =10, ω0 =1.0, ε =0.01,τ =0.1.
WhenP0>Pc,from the perspective of equivalent potential energy, the squeezing effect is stronger than the broadening effect, and the width of the DBW first compresses to a minimum value from the maximum value, and then gradually widens to the maximum value,as shown in Fig.1(a1). In Fig.1(a1),the force is less than zero at the input plane,it will be zero when the beam width is compressed to the narrowest,and the process of the beam broadening to the maximum will be relatively slow due to the loss effect,as shown in Fig.1(a2),
whereω=1 is a root ofV(ω)=0.
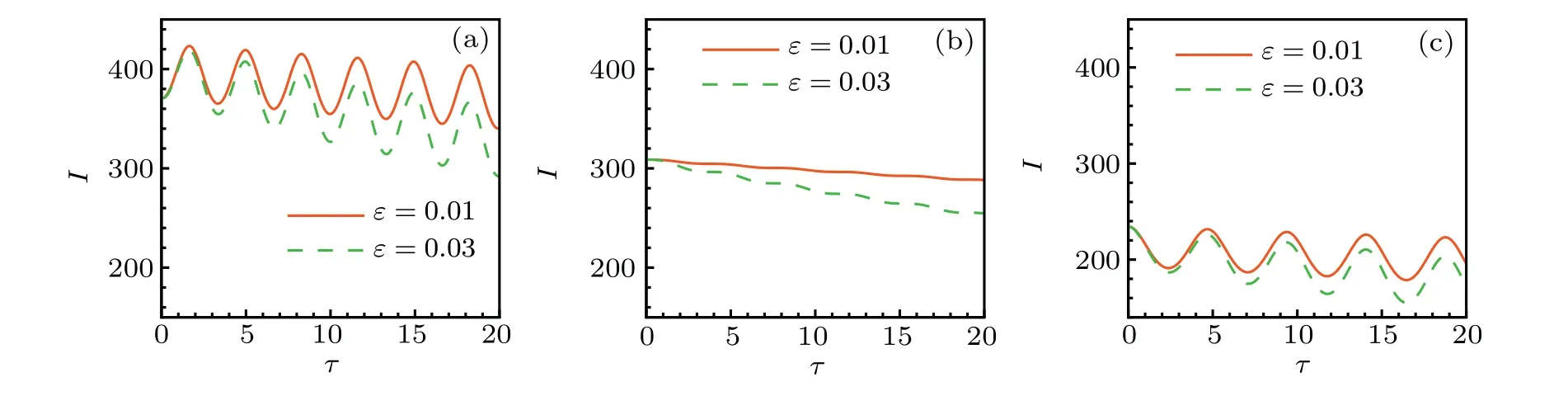
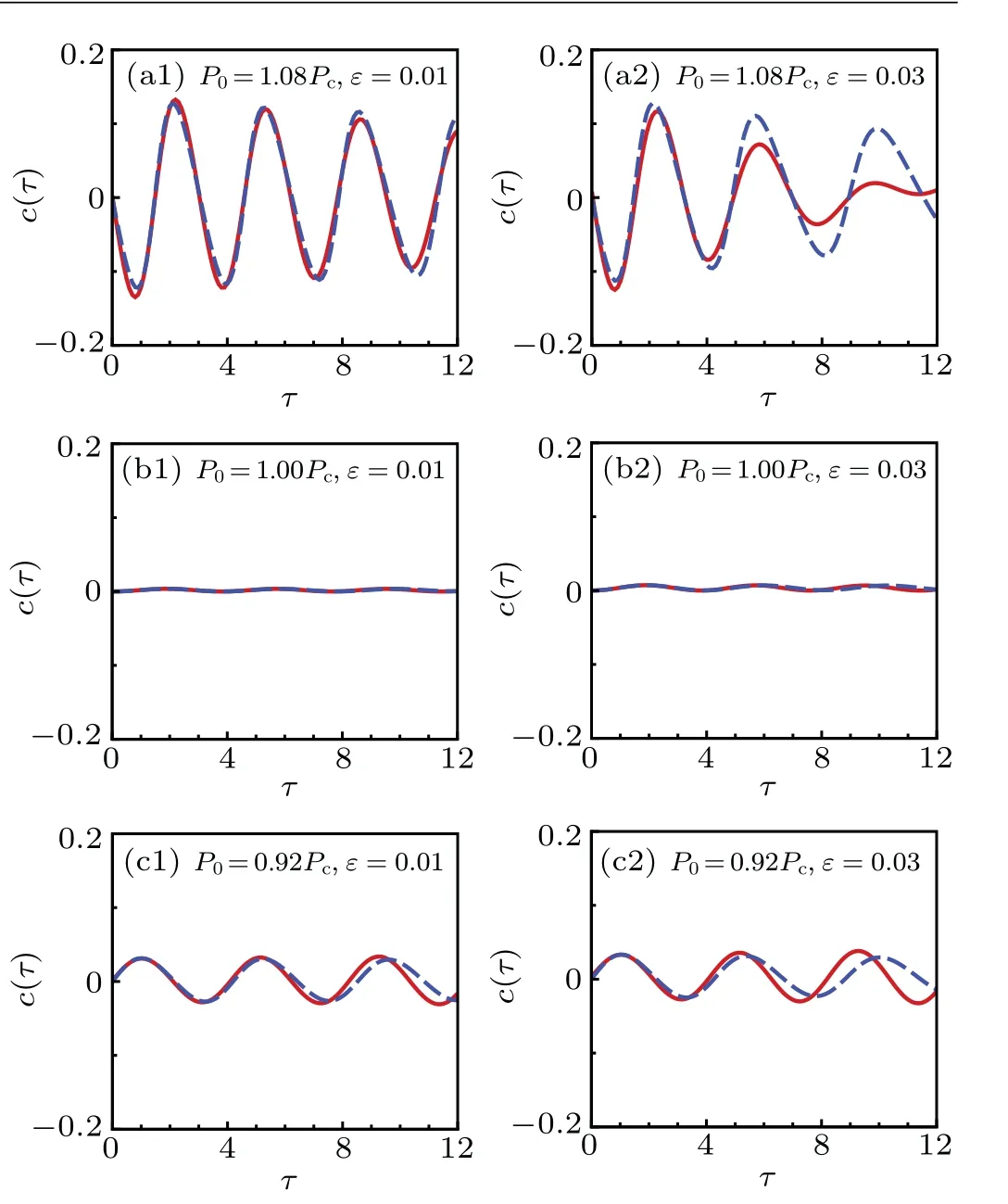
WhenP0=Pc,the broadening and squeezing of the beam are approximately equal,so the DBW propagates in a solitonlike state, and the equivalent potential energy and equivalent force are also zero at this time, as shown in Figs. 1(b1) and 1(b2). WhenP0 The force and potential energy can be regarded as the approximate harmonic motion by graphic analysis. We give the relationship between the equivalent force and potential energy and the propagation distance in Fig.2 to analyze the relationship more clearly. The power parameters are consistent with Fig. 1, with the increase of propagation distance, the equivalent force becomes smaller and smaller [Fig. 2(a)]. On the contrary,the equivalent potential energy becomes smaller and smaller[Fig.2(b)]. They are both monotone functions of the propagation distance at the given uniform loss. Fig.2. The equivalent force and equivalent potential energy varies with beam propagation distance under different incident powers. Other parameters are ωm=10,ω0=1.0,ε =0.01. Generally speaking,the loss factorεof the HNNM is relatively small, i.e.,ε ≪1, so we consider the approximation exp(-ετ)≈1-ετ.As a result,the influence of the loss on the change of the beam can be considered as perturbation. Hence,we obtainω(τ)=ω1(τ)+ω2(τ),whereω1(τ)is the solution of the beam width when loss is ignored. The beam width of the DBW satisfies a lossless equation in propagation. We can get a width of the DBW,and it can be written as AtP0/=Pc,ω(τ) is also divided into two parts, which tells us that considering loss of the media, the beam is oscillatingly widened regardless of the incident power. Thus, the analytical solution of beam widthω(τ)in the presence of loss is obtained. In order to demonstrate the validity of our analytical solution of the beam width, the numerical integration of Eq.(2)is carried out, the results are shown in Fig.3. One sees that the numerical integration based on Eq. (28) and the analytical result is approximate consistency,which shows our variable decomposition and the response function of the correctness of the approximation in Eq.(11). One can seen that no matter whether the situation isP0>Pc,P0=PcorP0 Fig. 3. Evolution of the DBW width ω(τ) in the lossy HNNM. Solid line: analytic result;dashed line: numerical integration based on equation initial. Other parameters are ωm =10, ω0 =1.0, P0 >Pc for(a1)and(a2),P0=Pc for(b1)and(b2),P0 Compared with the analytical results, the deviation between the analytical solution and the numerical solution becomes larger and larger with the increase of the propagation distance of the beam in the lossy medium. At the critical power, the incident DBW exhibits soliton-like propagation.Compared with low power, the analytical and numerical results of high power become better when the loss parameter increases. In order to ensure that the signal is not distorted,we can choose the appropriate distance and incident power to transfer information and energy, so as to avoid errors caused by low power and long distance. From the above results, we know that the critical power and incident power are different and the beam width is different,the subsequent parameters will also be different. Combining Eqs. (17)-(20) and (28), after some complicated calculations and simplifications,based on the beam width expression According to the above results,the evolution characteristics of the DBW can be analyzed after the beam intensity is affected by the loss in the propagation process. In Fig.4, we give the evolution process of the analytical and numerical results of the DBW intensity with the propagation distance. The corresponding numerical results are also presented in the form of three-dimensional graph in Fig.5. Fig.4. Evolution of the beam intensity I(τ)in the lossy HNNM.Solid line: analytical results;dashed line: numerical results. (a)P0=1.08Pc,(b)P0=1.0Pc,P0=0.92Pc. Other parameters are ωm=10,ω0=1.0. Fig.5. Numerical integration of the evolution of the beam intensity I(τ)in the lossy HNNM.Other parameters are ωm=10,ω0=1.0. Due to the existence of the loss, we can know that the DBW width becomes wider with the increase of the propagation distance, at the same time, the central DBW intensity decreases. When the input power is larger than the critical power, the DBW intensity shows the periodic weakening of the sine relation. When the input power is lower than the critical power, it shows the periodic weakening of the cosine relation. The evolution of the light intensity is similar to the periodic weakening of the spring linear harmonic oscillator.When the loss become larger, the central light intensity decreases dramatically,and the influence of the loss on the beam propagation is very obvious. WhenP0=Pc, we havec(τ)=c1(τ), the curvature can be obtained as follows: The evolution process of wavefront curvature is analyzed by comparing the beam width evolution diagram. The contrast between analytical situation and numerical situation for the wavefront curvature is given in Fig.6. The evolution state of the wavefront curvature is different for the varies powers.In the highly nonlocal environment, when the incident power is closer to the critical power and the loss is small enough(εless than 0.01),the comparison between the analytical and numerical results is more perfect,see the first column of Figs.6(a1)-6(c1). The results are no longer accurate within a short distance when the loss is slightly increased, see the second column of Figs.6(a2)-6(c2). WhenP0>Pc,the wavefront curvature evolution obeys the quasi cosine relation, and the radius of DBW curvature first decreases and then increases. WhenP0 Fig.6. Evolution diagram of the wavefront curvature c(τ). Solid line:analytical results. Dashed line: numerical results. (a) P0 > Pc, (b)P0=Pc,(c)P0 In summary,the propagation expression of the DBW in a lossy HNNM is derived by using the variational method, and the propagation characteristics of the DBW are discussed analytically and numerically. By properly selecting the incident power and the loss coefficient,we analyze the evolution of the beam width, the distribution of the light intensity, and the radius of curvature of the light field. The analytical results are compared with the numerical results, which well reflect the various propagation states of the DBW. In addition, we discuss the influence of loss on the process of information energy transmission. Due to the loss, the beam width of the DBW always expands as it travels farther independent of the input power. The evolution of the beam width is analogous to the relation of particle motion in classical mechanics. The theoretical analysis in this study lays the foundation for the experimental observation of the DBW. Acknowledgements This work was supported by the National Natural Science Foundation of China (Grant No. 12074098), the Natural Science Foundation of Hebei Province of China (Grant Nos.A2020205009 and F2020205016),the Science and Technology Project of Hebei Education Department,China(Grant No.ZD2018081),the Chunhui Plan of Ministry of Education of China (Grant No. Z2017020), and the Science Foundation for Distinguished Young Scholars of Hebei Normal University of China(Grant No.L2017J02).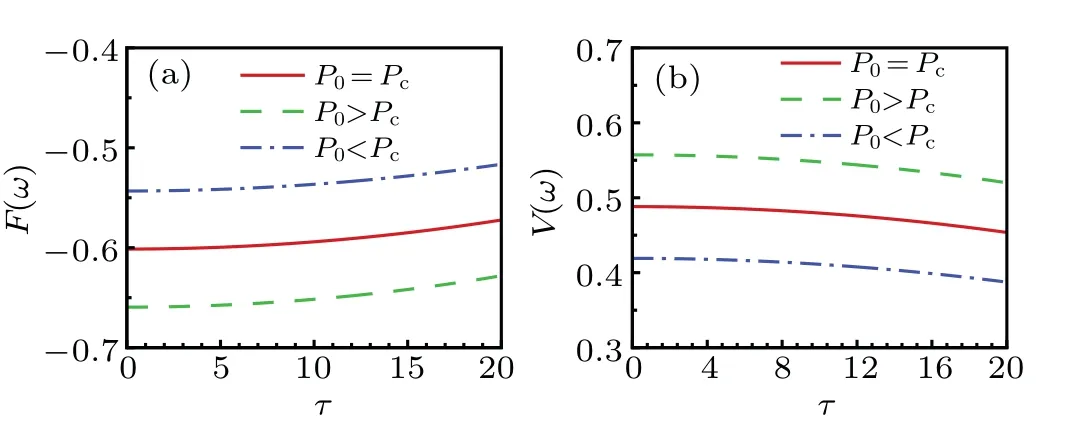
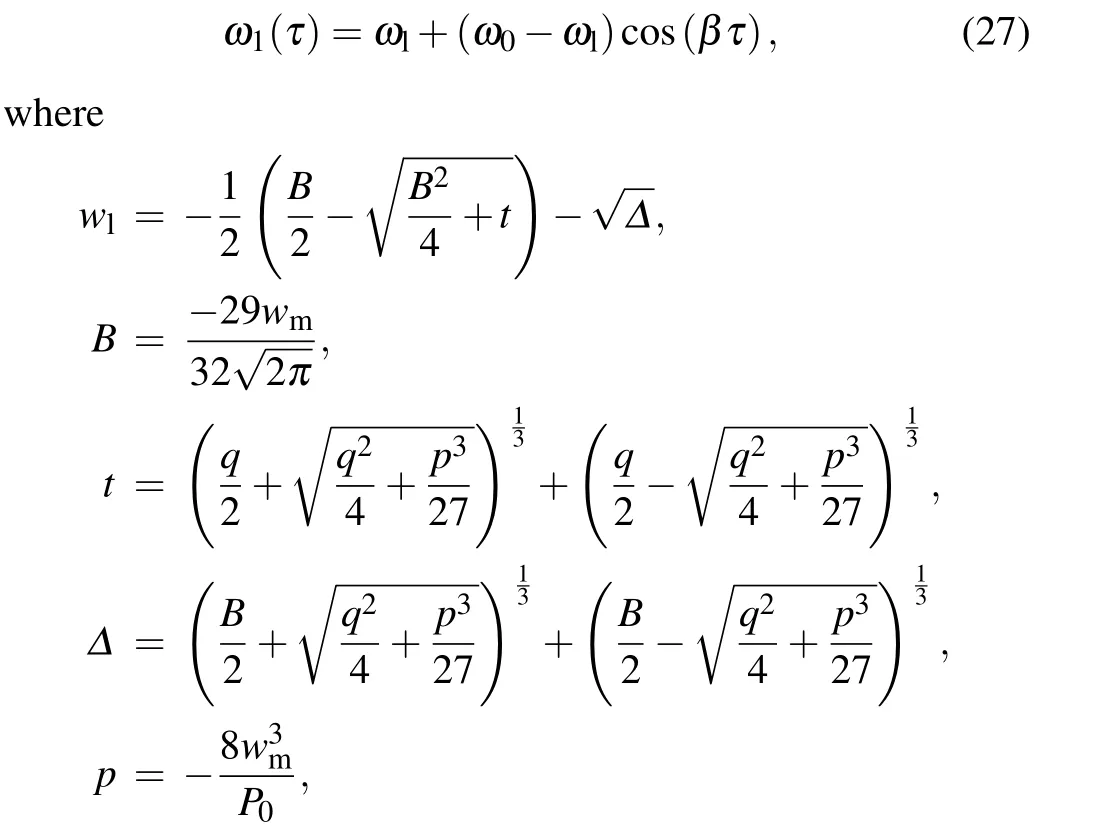







4. Summary
杂志排行
Chinese Physics B的其它文章
- Superconductivity in octagraphene
- Soliton molecules and asymmetric solitons of the extended Lax equation via velocity resonance
- Theoretical study of(e,2e)triple differential cross sections of pyrimidine and tetrahydrofurfuryl alcohol molecules using multi-center distorted-wave method
- Protection of entanglement between two V-atoms in a multi-cavity coupling system
- Semi-quantum private comparison protocol of size relation with d-dimensional GHZ states
- Probing the magnetization switching with in-plane magnetic anisotropy through field-modified magnetoresistance measurement
