Xilin Lu Zi-Min Li Vladimir V Mangazeev and Murray T Batchelor

1Department of Theoretical Physics,Research School of Physics,Australian National University,Canberra ACT 2601,Australia

2Mathematical Sciences Institute,Australian National University,Canberra ACT 2601,Australia

3Centre for Modern Physics,Chongqing University,Chongqing 40444,China

Keywords: light-matter interaction, hidden symmetry, asymmetric quantum Rabi model, asymmetric Rabi-Stark model

1. Introduction

The quantum Rabi model (QRM),[1,2]describing a twolevel atom interacting with a single mode bosonic light field,is central to a number of experimental platforms for the quantum simulation of light-matter interactions.[3-5]In the presence of a bias term, which breaks the parity symmetryinduced level crossings of the QRM, the system is described by the asymmetric quantum Rabi model (AQRM). It has been observed[6-11]that level crossings reappear in the spectrum of the AQRM when the bias parameterεtakes special values, indicating the existence of a hidden symmetry of the AQRM. Similar hidden symmetry has been observed in other AQRM-related models.[12]These generalized models include the asymmetric versions of the anisotropic QRM[13-15](the anisotropic AQRM)and the Rabi-Stark model,[16,17](the ARSM), where the special values of the bias terms are given by conditions on theεvalues, the so-calledε-conditions.[12]These observations indicate that the hidden symmetry in asymmetric light-matter interaction models is no coincidence,rather it is a general phenomenon. By investigating tunnelling dynamics in the displaced oscillator basis,a strong connection has been found between the hidden symmetry and selective tunnelling in the AQRM and the ARSM.[12]

A numerical study implied that any hidden symmetry operator of the AQRM must depend on the system parameters.[18]The way to construct the symmetry operator responsible for the hidden Z2symmetry of the AQRM was found recently.[19]This approach provides a cornerstone for constructing symmetry operators in related models. In this article,making use of an ansatz based on the AQRM results,we determine the symmetry operators for the other AQRM-related models under theirε-conditions.[12]We begin with a brief review of the AQRM results and propose the ansatz based on these results in Section 2. This ansatz is used to calculate the Z2symmetry operatorsJfor the anisotropic AQRM and the ARSM in Sections 3 and 4,respectively. In Section 5,we discuss the combined anisotropic ARSM.Concluding remarks are given in Section 6.

2. Hidden symmetry in the AQRM and general ansatz

The AQRM is defined by the Hamiltonian

Depending on the corresponding eigenvalues of the parity operator, energy levels of the QRM separate into two distinct sectors,with crossings only between levels from different sectors.

Theε-condition for the AQRM is whenε=M/2 for some integerM.At these special values,crossings between different energy levels are observed in the spectra. The correspondingJoperators were found in Ref.[19](see also Ref.[20]). These symmetry operators take the form of 2×2 matrices of polynomials inaanda†, where the degree of the polynomials is equal toM. As examples, the caseM=0 simply gives the parity operatorPand the caseM=1 gives

whereai,j,bi,j,ci,j,di,jare constants needing to be determined.

The process of calculatingJoperators for a specific model is straightforward. First we need theε-condition for crossings to appear,this can be obtained by exploring the pole structure of Braak’sG-function[6]appearing in the analytic solution. Then we solve the matrix equation

at different values ofεto determine the values for constants,giving the expression for theJoperator.

It needs to be emphasized that this method is on a caseby-case basis and that we cannot obtain general formulae for arbitraryM. In fact, it is still an open question, even for the AQRM case,if it is possible to find the general formula for theJoperator.

3. Anisotropic AQRM

We start with the anisotropic generalization of the AQRM. The anisotropic AQRM[12]allows for the tuning of the relative weightλbetween rotating and counter-rotating terms. An example application of such a tuning is the electronic spin-orbit interaction in semiconductors, where the Rashba and Dresselhaus spin-orbit interactions act like the different rotating terms under certain transformation.

The anisotropic AQRM Hamiltonian is

We see that the expressions for theJoperators quickly become cumbersome asMincreases. For this reason we only include theM=1 case for the other models covered in the following sections.

4. Asymmetric Rabi–Stark model

Another model that we discuss here is the ARSM, with Hamiltonian

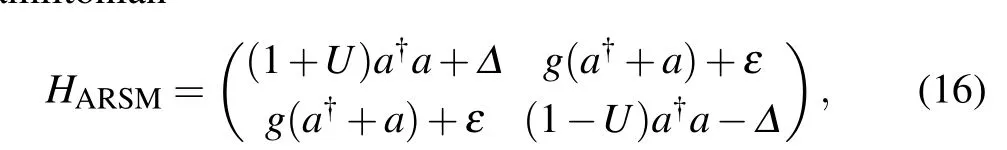
where we have added the Stark termUa†aσzto the AQRM Hamiltonian(1). Interestingly,this Stark term is adjustable in the Grimsmo-Parkins scheme[21]for the cavity quantum electrodynamics realization. Without the biasε,this model has Z2symmetry and has been exactly solved.[16,17]Special behavior such as selective interactions[22]have also been explored.However, with the bias term the symmetry is again broken,which makes the analysis much harder, unlessεsatisfies theε-condition.

Note that we need|U|<ω=1 here to avoid unphysical results.[17]We therefore re-parameterizeU=sintto simplify later expressions. Under this parametrization, theεcondition[12]for this model isε=(M/2)cost. For theM=1 case, using the same method as above, we arrive at the symmetry operator

As expected, this result simplifies to the AQRM case whent=0.

TheJoperators for the ARSM again square to polynomials ofH. However, the interesting point here is that theseJoperators have a relation of order 2Mwith the Hamiltonian instead of orderMfor the AQRM case. For example,

5. Anisotropic asymmetric Rabi–Stark model

Recently the anisotropic Rabi-Stark model is also drawing some attention.[23]Knowing results for the special cases of the asymmetric version,it is worth establishing the symmetry operator for the anisotropic ARSM.The Hamiltonian for this rather complicated model is

which is simply the combination of ingredients.

Following the same steps as before,we obtain

From the previous sections,we know that only the Stark term produces extra orders in the relation betweenJandH.Therefore, theJoperators for the anisotropic ARSM follow similar 2M-order relations with the Hamiltonian as the ARSM cases(19)and(20).

6. Conclusion and discussion

In this paper we have demonstrated that the recent results for the AQRM Z2symmetry operator can be generalized to other AQRM-related models, namely the anisotropic AQRM,the ARSM,and the anisotropic ARSM.This confirms that the existence of hidden symmetry is a general phenomena, and not restricted to the AQRM. The method we have used is to assume that the underlying symmetry operatorsJtake similar forms as the AQRM case. The explicit form for this ansatz is given by Eq.(8). Starting with this ansatz,we have calculated the constants involved by solving the matrix equation(9).This process is straightforward to perform but does not give a general expression. The procedure therefore needs to be repeated for each value ofMand for each model. We also show thatJ2Mis a polynomial in terms of the Hamiltonian,which defines the Z2nature of the symmetry. Curiously, the degree of the polynomial can be affected by the terms added to the AQRM.Here we saw that the Stark termUa†aσzchanges the polynomial degree fromMto 2Mwhile the anisotropic parameterλmakes no change.

There are still many questions to explore. For example,how far can the AQRM be deformed while preserving the hidden symmetry, and what are the underlying mathematical structures?[24]In other work,[25]we have studied the multiqubit generalization of the AQRM, also known as the biased Dicke model. We found that only the lowest non-trivial order (M= 1) of the hidden symmetry is present, which we believe is due to the interference between atoms. In another direction, the multi-photon AQRM has also recently been investigated,[26]where hidden symmetry with various orders was observed. Surprisingly, the spectral curve crossings appear in the three-dimensionalE,g,εplot instead of the usualE,gplot. It will also be very interesting to look at the underlying symmetry operator structure of this model. Symmetry operators have now also been constructed within the Bogoliubov operator approach.[27]We conclude by emphasizing that a precise physical interpretation of hidden symmetry operators remains to be determined, even for their simplest manifestation in the AQRM.

Appendix A:Collection of formulae

In this Appendix we collect some of the more lengthy results. For the anisotropic AQRM, the operators appearing in Eq.(14)are

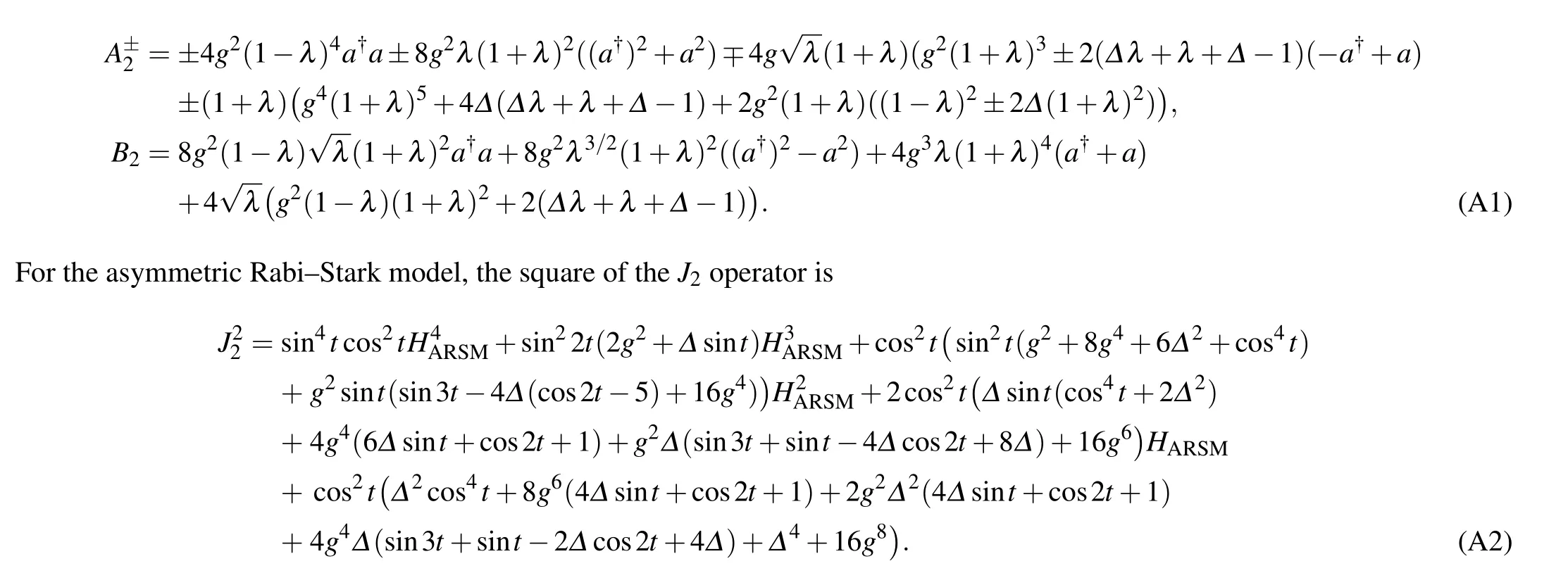
Acknowledgement

Project supported by the Australian Research Council(Grant Nos. DP170104934 and DP180101040).