Shun Wang(王顺) and Wei-Chao Jiang(姜维超)

College of Physics and Optoelectronic Engineering,Shenzhen University,Shenzhen 518060,China

Keywords: time-dependent Schr¨odinger equation(TDSE),smooth exterior complex scaling(SECS)absorbing method,Arnoldi propagator

1. Introduction

In the study of ultrafast atom-laser interactions in modern strong-field physics and attosecond science,many simulations are based on the numerical solutions of the time-dependent Schr¨odinger equation (TDSE).[1-6]In cases where the laser pulses or the time-delays between the laser pulses are extremely long, the numerical TDSE calculation can be rather challenging. The methods to absorb the out-going electron wave packet are critical for the efficient simulations involving long-time propagation. The mask function[7,8]and the complex absorbing potential(CAP)[9-11]are two classes of widely applied absorbing methods. Such methods have the advantage of easy implementation,but they usually do not guarantee the complete absorption and sometimes the noise from the refection at the absorbing point can disturb the physical signal. On the other hand,the more complex absorbing methods with better absorption efficiency, such as the perfectly matched layer(PML)method[12-14]and the exterior complex scaling(ECS)method,[14-20]have also been applied in the numerical TDSE calculations.

The ECS method originates from the complex scaling(CS) method, in which the radial coordinate of the electron is scaled by a complex phase factor. In the early years,the CS method was applied to establish the analytic properties of theS-matrix in the complex momentum and energy planes[21,22]and to describe the resonance states.[23]In 1979,Simon[24]introduced the idea of ECS as an extension of the CS method.In the ECS method,the radial coordinate is kept real for small values, whereas for values larger than the absorbing pointr0,CS is performed. In this way,the energies of the bound states in the field-free atomic system are unchanged, but that of the continuum states are rotated downwards by an angle in the complex energy plane and the continuum wave functions are rendered square integrable. The application of ECS as an absorber for the out-going wave is built on a solid mathematics ground.[23-26]The extension of the ECS to numerical TDSE calculations was demonstrated by McCurdyet al.[27-29]Most authors took the sharp ECS method[14,16-20]and finite-element discrete variable representation(FE-DVR)in their TDSE calculations. The word “sharp” means that the scaling atr0is not continuous. In the FE-DVR frame,the discontinuity of the sharp ECS can be correctly handled as long asr0is taken to be the bridge point of two adjacent elements. In 2009,Taoet al.[19]reported a drawback of the ordinary ECS:the numerical error accumulates for long-time propagations and can only be controlled by extending the grid points. Recently, Scrinziet al.[14,16,30]developed the infinite range exterior complex scaling(irECS)which promises to overcome such drawbacks.

In the early applications of the CS method in timeindependent calculations, the Arnoldi (Lanczos) method was often used to calculate part of the eigenvalues of the corresponding non-Hermitian Hamiltonian.[31-33]The Arnoldi method was developed to be an efficient propagator in the time-dependent calculations by Park and Light in 1986.[34]Now Arnoldi propagator is popular in the simulations of highdimensional systems such as two-electron atoms[4,35-38]and two-electron molecule H2.[39,40]However,in a recent calculation of double ionization of helium[41]by IR laser pulse using irECS method, a pessimistic judgement on the efficiency of Arnoldi propagator was made and Arnoldi propagator was finally given up in their study. In our recent work,[42]we showed that the Arnoldi propagator can be used for the strong IR laser pulses after proper modifications. In this paper, we will show that the Arnoldi propagator can be combined with the ECS method after additional modifications. We choose the smooth exterior complex scaling (SECS), instead of the sharp ECS, as the absorber. SECS has previously been developed in the time-independent calculations of the resonance states.[43,44]In comparison with the sharp ECS, we do not need to be worried about the discontinuity at the CS pointr0and the limitation thatr0must be a bridge point of two elements is not necessary in the SECS method. The application of sharp or smooth ECS leads to a non-Hermitian Hamiltonian matrix, whose eigenstates are not orthogonal as the usual inner product. Thus, the usual application of Arnoldi(or Lancozos)propagator for Hamiltonian matrix with Hermitian symmetry should be modified properly to take account of the general non-Hermitian symmetry. We report the modifications to these numerical methods and test them in the threedimensional TDSE of single-active-electron(SAE)atom. We demonstrate that SECS can be a wonderful absorber by tracking the propagation of the electron wave packet. Meanwhile,the developed Arnoldi propagator for non-Hermitian Hamiltonian is quite stable and efficient even if strong IR laser pulse is used. Classical quiver motion of the freed electron in the strong IR laser pulse is clearly identified from the timedependent radial distributions of the freed electron. To our knowledge, the successful combination of ECS and Arnoldi propagator for solving the TDSE has never been reported before.

Unless stated,we will adopt atomic units in this paper.

2. Theory

2.1. Time-dependent Schr¨odinger equation

The TDSE of the three-dimensional SAE atom is given by

The time-dependent electron-laser interaction Hamiltonian is given by

2.2. Smooth exterior complex scaling

The SECS method is applied to scale the radial wave functions in Eq. (6). We map the real radial coordinaterto the complex variableuaccording to[44]

In the numerical implementation,however,the smooth parameteracannot be too large in case the overflow takes place for the term cosh[a(r+r0)] or cosh[a(r-r0)]. One example of SECS is provided in Fig. 1. The complex coordinateuas a function of the real radial coordinateris shown in Fig. 1(a),and its derivative with respect toris shown in Fig.1(b).

Fig.1. (a)The complex coordinate u and(b)its first derivative du/dr as a function of the real radial coordinate r in the SECS[Eq.(9)]. The CS point r0 is 40 a.u.,the CS angle η is π/6,and the parameter a is 2.0 a.u.

The radial wave functionsRlm(r,t) are analytically extended into the complexuplaneRlm(r,t)→Rlm[u(r),t]. In order to simplify the expression of the volume element duto be equal to dr, the following new radial wave functions are defined:

In numerical implementation, the radial functionsRlm(r,t) are further expanded in terms of the FE-DVR basis functions.[45]After applying SECS,the Hamiltonian matrixHis scaled to be a complex symmetric matrix.

2.3. Non-Hermitian Arnoldi propagator

In this subsection,we present the non-Hermitian Arnoldi propagation algorithm to solve the differential Eq.(12),which is still identical to the general form of TDSE[Eq.(1)],except for that the Hamiltonian matrixHis not Hermitian any more.The goal is to obtain the wave functionΨ(t+Δt)in the next small time step when the wave functionΨ(t) at momenttis known,i.e.,

The Arnold algorithm differs from the Lanczos algorithm in the way to obtain orthonormal basis vectors|qi〉and the corresponding matrix elements of the Hamiltonian. The Lanczos algorithm is based on the fact that the Hermitian matrix in the Krylov subspace is tridiagonal. In this paper, we choose the more general Arnold algorithm[46]to treat the non-Hermitian Hamiltonian matrix. Though the scaled Hamiltonian matrixHis complex symmetric in the full FE-DVR space, such symmetry is not kept in the representation of Krylov subspace.The application of the Arnold algorithm results in a complex upper-Hessenberg Hamiltonian matrix,

andA-1denotes the inverse matrix ofA. We would like to stress that the matrix inversion in the numerical implementation is not necessary if the Hamiltonian is Hermitian,sinceAcan be simplified to a unit matrix in that case. The fact thatAis not a unit matrix is one important difference between the present propagator for general non-Hermitian matrix and the pervious propagator for Hermitian matrix.

Now we can approximate the short-time propagation Eq.(19)in the Krylov subspace as

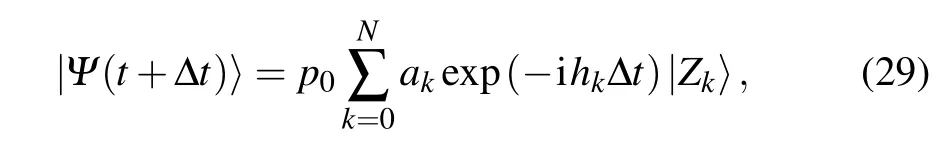
wherep0is defined in Eq. (24). When max[real(hk)] is large, one can split the centrifugal potential from the whole Hamiltonian to reduce max[real(hk)],as reported in our recent publication.[42]In the rest of the paper,if not stated otherwise,the whole radial box is discretized uniformly, each finite element having a size of 2 a.u.and being represented by 8 basis functions.

3. Tests for XUV laser pulse

In this section, we mainly test the applications to simple weak XUV laser pulse, where the electron dynamics can be simply predicted by the first-order perturbation theory. We adopt an XUV laser pulse with peak intensity 1012W/cm2,photon energyω=53.6 eV (which is much larger than the ionization potential of atomic hydrogen,Ip=13.6 eV ), and total duration of 10 optical cycles. The bound electron is freed by absorbing one photon,leaving the nucleus with kinetic energy of 40 eV or momentum of 1.7 a.u. To study the behavior of the out-going electron wave packet when it approaches the CS pointr0,we analyze the following angular-integrated timedependent radial distributions after subtracting the component of the ground-state from the whole wave function:

The time-dependent radial distributionD(r,t)is shown in Fig.2.In the first and the second rows in Fig.2,one can clearly see that the freed electron packet moves to larger radius as the time increases. The slope of the peak signal is exactly the photoelectron momentum(1.7 a.u.). In all the panels applying SECS in Fig.2, the CS pointr0is fixed at 40 a.u. In the first row in Fig. 2, we check the influence of the width of the CS layer,rc, on the absorption efficiency. The width is given byrc=rmax-r0,wherermaxis the full size of the radial box.The results for two differentrcare shown in Figs.2(a1)and 2(a2).As a comparison, the benchmark full result, where no SECS is applied andrmaxis large enough, is shown in Fig. 2(a3).One can see that for the present simple one-photon ionization,the widthrc=5 a.u. is large enough to guarantee the perfect absorption[Fig.2(a2)]. In Fig.2(a2),it is clear that the electron signal quickly decays after the electron passes through the critical scaling pointr0, and no disturbance exists for radius smaller thanr0in comparison with the benchmark full result shown in Fig.2(a3). On the other hand,obvious reflection can be identified ifrcis extremely small(1 a.u.) as shown in Fig.2(a1). More strict comparisons between the results of SECS with differentrcand benchmark“full”result are given in Fig. 2(c1), where the cut lines ofD(r,t) att=38 a.u. are shown. The SECS result forrc=5 a.u.agrees with the benchmark full result perfectly forrr0.

In the second row in Fig.2,we check the influence of the scaling angleη,which appears in Eqs.(9)and(10).ηshould be chosen in the range [0,π/4]. Takingη=0 is identical to canceling the SECS absorber. Three different values ofηare chosen in the second row in Fig.2. One can find that the absorption efficiency is not sensitive to the choice ofηas long as the CS layer is wide enough. In Fig.2(c2),the cut lines ofD(r,t)att=38 a.u.are shown for differentη. These cut lines agree with each other perfectly forrr0. As expected, the value ofηhas an influence on the decay rate, i.e., the largerηcorresponds to the faster decay.

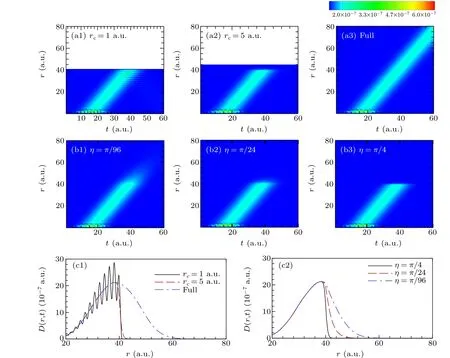
Fig.2. The angular-integrated time-dependent radial probability density D(r,t)[Eq.(30)]for different(a)widths rc of the CS layer and(b)CS angles η in one-photon ionization of atomic hydrogen by weak XUV laser pulse at photon energy of 53.6 eV.In all SECS calculations,the CS point r0 is fixed to be 40 a.u. In(a),η =π/6 is taken. In(b),rc=40 a.u.is taken. The cut lines of D(r,t)at t=38 a.u.are shown in(c). The contribution of the ground state has been subtracted from the whole wave function.

4. Tests for strong IR laser pulse

The TDSE calculation for the strong IR laser pulses is much more challenging than that for the XUV laser pulses.The amplitudeα0of the classical quiver motion of the free electron in the monochromatic laser field can be rather large in the strong IR laser pulse. The freed electron can be driven back by the external strong IR field. One problem we would like to explore here is whether the value of the scaling pointr0can be significantly smaller than the amplitudeα0of the quiver motion of the freed electron. The quiver amplitudeα0is given by

whereA0andωare the amplitude of the vector potential and the central frequency of the laser pulse, respectively. In the following tests,we take the laser pulse with peak intensity of 1×1015W/cm2and wavelength of 780 nm, and the quiver amplitudeα0is evaluated to be 49.5 a.u.

To trace the quiver motion of the freed electron in the field of the strong IR laser pulse, the angular-integrated radial distributionD(r,t) defined in Eq. (30) is not a good physical quantity since the quiver motion of electron is angularly distinguished. Therefore, we directly study the timedependent probability density along the laser polarization direction,which is defined by

Similar to Eq.(30),the component of the ground state has been subtracted from the whole wave function.

The time-dependent electron distributionP(z,t)is shown in Fig. 3. In Figs. 3(a) and 3(b), the SECS result withr0=200 a.u.and the benchmark full result are shown,respectively.The quiver motion of the freed electron in the external strong IR laser field can be identified clearly and the peak signal of the probability density precisely mimics the time-dependent electric field of the IR laser pulse. Different from the purely outgoing electron motion in the field of XUV laser pulse as shown in Fig.2,the electron in the field of strong IR laser pulse can be driven back towards the nucleus. In opposite to the outgoing electron wave packet,the in-coming electron wave does not decay in the complex layer.

We have calculated electron distributionsP(z,t)with various absorbing pointr0but the same radial box sizermax=260 a.u., and the corresponding cut lines of the distributionP(z,t) att=201 a.u. are shown in Fig. 3(c). As tested, the minimum width of the CS layerrcrequired for convergence is about 80 and 10 a.u.forr0=80 and 200 a.u.,respectively.Forr0smaller thanα0=49.5 a.u.,the total population of the electron in the whole space,i.e.,〈Ψ(t)|Ψ(t)〉,can grow from 1 to an extremely huge number and the numerical result completely makes no sense. In Fig.3(c),we can see that the SECS result forr0=60 a.u.does not produce correct result forr

Fig. 3. The time-dependent angular-distinguished radial probability density P(z,t) [Eq. (32)] from (a) SECS calculation with r0 =200 a.u.,rmax=260 a.u.and(b)benchmark full TDSE results with enough large box for a sin2-shape IR laser pulse at wavelength of 780 nm,intensity of 1×1015 W/cm2 and duration of 3 cycles. In(b),the time-dependent electron field of the IR laser pulse is also shown as a red solid line. The cut lines of P(z,t)at t=201 a.u.are shown in(c)for different CS points r0 but the same radial box size rmax=260 a.u. Similar to Fig.2,the contribution of the ground state has been subtracted from the whole wave function.

Here,we would like to provide a comparison of the SECS with another often-used absorber - the traditional wavesplitting absorber. In the latter scheme,at each time iteration,the electron wavefunction is multiplied by an absorbing function in the form of

where the absorbing point is also denoted withr0, andσis a constant parameter the value of which should be properly chosen. By such multiplication, components of the high-energy electron in the wavefunction are smoothly discarded.Comparison of the angular-distinguished radial probability densitiesP(z,t) att=201 a.u. obtained with the SECS and the wavesplitting absorber is shown in Fig.4.r0and the radial box sizermaxare kept the same for both absorbers. Whenr0=80 a.u.,rmaxandσare set to be 160 and 30 a.u., respectively. The result obtained with the wave-splitting absorber deviates substantially from the SECS result (which is convergent as examined). Whenr0is increased to 200 a.u., wherermaxandσare respectively set to be 210 and 3 a.u., results obtained using both absorbers coincides with each other. Apparently,the SECS has better absorbing ability than the wave-splitting absorber,since the former can realize perfect absorption even whenr0is rather small. The present work is partly inspired by the paper on the irECS absorber.[16]In the irECS scheme,the CS layer contains only a small number of discretization points,yet perfect absorption is still realized. To examine whether the SECS absorber could use much coarser discretization in the CS layer, we recalculate the curve obtained using the SECS absorber in Fig.4(a)with larger element size forr>r0while the element size forrr0is limited.To reach the high efficiency of the irECS absorber by using very coarse discretization in our method,technical challenges remain to be overcome.

Fig. 4. Comparison of the angular-distinguished radial probability density P(z,t) at t =201 a.u. obtained using two different absorbers - the SECS and the wave-splitting absorber. (a) r0 = 80 a.u., rmax = 160 a.u.; (b)r0 =200 a.u., rmax =210 a.u. Laser parameters are the same as those in Fig.3.

Fig.5. Comparison of the angular-distinguished radial probability densities P(z,t) at t =200 a.u. for different time steps Δt obtained using the modified (non-Hermitian) Arnoldi propagator (a) and Runge-Kutta propagator(b). The radial box size is 260 a.u. and r0 =200 a.u. Laser parameters are the same as those in Fig.3.

To demonstrate the propagation efficiency of the proposed non-Hermitian Arnoldi propagator, we test its maximum time step Δtrequired for convergence against that of the 4th-order Runge-Kutta propagator[Fig.5]. In both cases,the SECS absorber is adopted for absorption, and the radial box size is chosen to be 260 a.u., andr0=200 a.u. The order of the Arnoldi propagator is set to be 8, an often-used order.For both absorbers, the order equals to how many times the Hamiltonian is multiplied with the wavefunction, and these multiplications are the major computational cost. As can be seen in Fig. 5, for the non-Hermitian Arnoldi propagator the maximum Δtrequired is between 0.0129 a.u. and 0.013 a.u.,while in the Runge-Kutta case the maximum Δtlies between 0.00522 a.u. and 0.00525 a.u. The maximum Δtallowed in the former case is approximately two times of that in the latter case. As a result, the two propagators have comparable efficiencies. Traditionally, the Arnoldi propagator has been considered more efficient than the Runge-Kutta one. However,in a recent work on double ionization by IR fields,[41]where the irECS was used as the absorber, the authors found that the Arnoldi propagator has no advantage in efficiency over the Runge-Kutta. Our work provides a similar observation. Finally, we would like to stress that, in all the calculations in this work,the centrifugal potential is split out from the whole Hamiltonian by using the scheme we proposed in Ref. [42],which greatly improves the efficiency of time propagation of the wavefunction. It is under this condition that our comparison of the two propagators is done.

5. Conclusions

In this work, we have successfully combined the SECS and non-Hermitian Arnoldi propagator to efficiently solve the three-dimensional TDSE of the SAE atom. The timedependent angular-integrated and angular-distinguished radial distributions of the electron are calculated. From these distributions,the absorption of the out-going electron wave packet and the quiver motion of the freed electron in the field of strong IR laser can be clearly observed. We have shown that SECS can be a perfect absorption method as long as the CS radial coordinater0and the width of the CS layer are properly chosen such that its absorbing ability surpassing that of the traditional wave-splitting absorber.When the strong IR laser pulses are used, one should be careful that the scaling coordinater0should be significantly larger than the amplitude of the quiver motion of the freed electron.The non-Hermitian Arnoldi propagation method we developed is stable not only for weak XUV laser pulses but also for strong IR laser pulses. Its efficiency is found to be comparable to that of the Runge-Kutta propagator,supporting the discussions in Ref.[41].The numerical scheme proposed in this work is particularly useful in simulations requiring long-time propagation. It may also be useful for more complex systems with electron correlations. At last,the modified Arnoldi propagator has the potential to be combined with the irECS absorbing method.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.12074265 and 11804233).